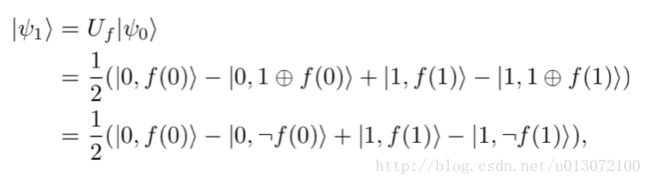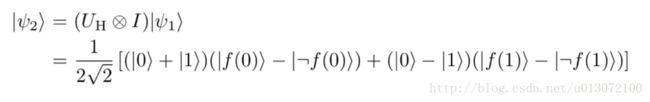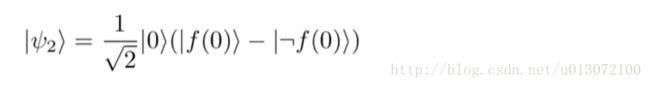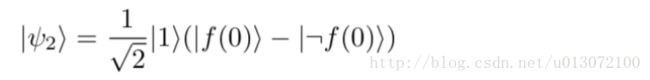量子计算机简介

以下有些表述可能不那么严谨，毕竟只是一个科普。不过如果发现有不对的地方，还是希望可以提出来，指正或者一起探讨。主观表述仅代表个人看法。

1 几个问题

1. 现在有没有量子计算机？
   严格的说，截止到2018年1月，没有。

2. 那D-Wave是什么？
   是一家加拿大声称做量子计算机的创业公司，截止现在为止卖出去两台，一台被google买走、一台被Lockheed Martin买走，并且不是通用计算机，只解决一些寻找极值的优化问题，并且核心部件工作在极端低温的环境下，20 mK。对这台机器的具体工作模式，公司自己也表示解释不太清楚。后面会详细说一下这中间的争议，已及他们对探索量子计算机的贡献。
   20 mK是什么概念，-273.15 K是绝对零度，20 mK只比绝对零度高0.02度。

3. 物理领域以及计算机领域的科学家对量子计算机什么看法？
   计算机领域有持悲观态度的，认为瞎搞。比较活跃的还是物理领域的科学家，但没人能够很肯定的说出用多长时间可以造出一台真正的量子计算机来。

4. 如果有量子计算机，使用者需不需要明白量子力学？
   不需要。就像我们现在用计算机的人，即便是做上层工程以及算法的，又有几个人真正清楚计算机是怎么工作的呢？

5. 量子计算机的优势？
   降低一些问题的时间复杂度。

2 量子计算机及其理论基础

量子计算机的概念是在1980年代开始比较多的讨论。为解决物理问题，需要用传统的计算机模拟量子现象，但数据空间会很大，那如果有一个基于量子现象构造成计算机的话，它就可以天然的表示量子状态，而不需要去模拟。比如一个粒子的自旋有两种状态和，如果用传统计算机去模拟，那我们就需要两个比特去描述；假如我们有一个基于粒子自旋的状态构造成的一个计算机，那我们用一个自旋比特就够了。

以上说的其实就是一个概念，至少在2000年以前没人知道怎么实现这样的一个事情。从概念到可操作的量子计算机之间有一个很大的gap，如果你对我们现在的计算机的构造有了解的话，就会明白量子计算机有着不同于我们现在熟知的计算机的体系结构，通俗的说就是这种计算机有另一种工作原理。

下图示意了经典计算机与量子计算机的区别。会着重讲一下绿色对应的两部分，上层应用及底层实现。

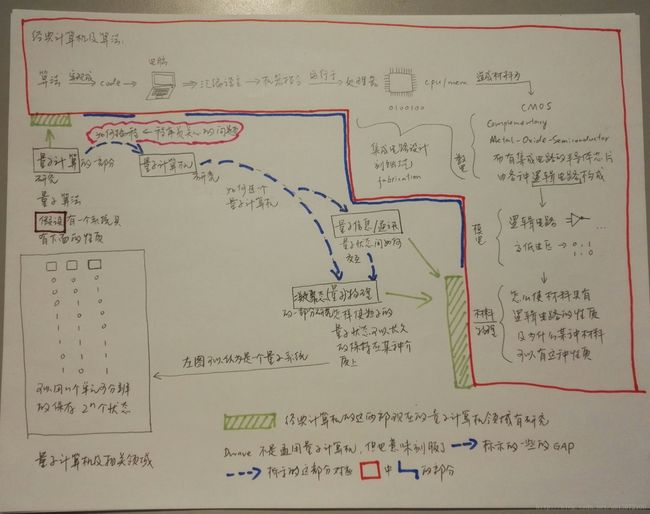
第一台计算机出现在1946年，无论是底层的硬件还是上层的应用都和我们现在看到的计算机有很大的差别，但是基本原理是一样，就是用可控制的0和1来完成任务的。下图中红色框内所示意的是现在基于硅半导体材料制作的芯片的计算机。

量子计算机的概念自从提出以来，大多数的研究集中在理论研究上，就是假设现在已经有一种系统可以承载想要的这些量子状态所具有的性质，并且也假设了对这些量子状态的操纵可以通过算子(operator)来实现，通俗的说现在有两个可互相转变的状态 |ψ⟩ 和 |ϕ⟩ ，则存在幺正变换(unitary transformation)U使 |ϕ⟩=U|ψ⟩ ，幺正变换是可逆的这个U就叫做一个算子(operator)，把U和 |ψ⟩ 的一次相乘就叫做一个操作。量子算法就是说我已经有了这样的一些状态 |ψ⟩ ，以及一些可以满足我需要的算子U，这些状态之间可以线性叠加，这些算子可以操作状态，算法就是通过把一个问题的初始状态通过设计映射到这些状态可以表示的形式，然后通过一系列的算子操作及叠加运算，使得这些初始状态可以变换到期望的final state，最后通过测量这个final state得到问题的答案。

这个状态该怎么理解呢？拿自旋来说，再具体一点，以电子的自旋为例，一个物理事实是电子具有自旋，并且只有两种状态，向上和向下，在物理中一般用 |↑⟩ 和 |↓⟩ ， |1⟩ 或 |0⟩ 和表示，这些是算符表示，可以等价的用向量来表示，就是

(10)

和

(01)

，在量子力学中就可以把一个电子自旋维度的状态表示成 |ψ↑↓⟩=α|↑⟩+β|↓⟩ 或 |ψ↑↓⟩=α|1⟩+β|0⟩ 或

|ψ↑↓⟩=α(10)+β(01)

，一般就把一个状态表示成这个状态所有可能情况的线性叠加，一次操作U是同时作用在这些不同的叠加分量上的。量子力学中认为一个微观状态在测量之前，它就是一个各种可能状态的叠加，在测量这个不可逆的操作干扰之后，它才回塌缩到可能存在的状态中的一种。测量操作不是一个幺正变换。
后面会简单的介绍一个量子算法Deutsch Algorithm, 其它的Deutsch-Jozsa Algorithm, Grover’s Search Algorithm，Quantum Fourier Transform和Shor’s Factorization Algorithm可以去看参考书。

那为什么量子力学中认为一个微观状态应该表示成各种可能状态的叠加而不是其中的某一个呢？就把这个当做一个物理事实就好了。在量子力学的建立过程中，物理学家们也想了很多假想的实验去challenge这个理论，或真正的实验和观测去验证这个理论，到现在为止，量子力学对解释我们生活的宇宙有合理的贡献，也逐渐被大多数的人认可，成为了物理学科的一块基石。

3 量子计算机的实践之路

说了这么多大部分还只停留在理论层面，那如何去制备这些量子状态呢，我们该用什么样的环境、什么样的材料，该如何去操作？这就需要实验物理学家去努力了。

去制备这些量子状态，基本上有两个方向，光学和凝聚态。光学系统在量子通讯中比较重要，有人也假想过用光学系统去造量子计算机，这里面起作用的是光子；量子计算领域的凝聚态方向包括半导体和超导，用半导体和超导材料去制造量子计算机是目前主要尝试的方向；但也有可能未来的量子计算机采用的是完全不同的一种方案。

上面这些图片来自D-Wave的资料，在一些介绍量子计算机的场合经常会看到类似这样的图片，其实核心部件是上面左图片中的QPU芯片，那为什么有其它的部件？是需要这些设备把芯片周围的环境温度降到几十mK。

右面这张是QPU的放大图。这些是量子计算机成败最重要部分。

4 首个所谓的商业量子计算机D-Wave

既然D-Wave说他们造出来了，虽然有争议，但也是先驱，关于他们的资料也是最多的，就以他们为例来说一下他们这里所谓的“量子计算”。在D-Wave的官方材料中是以Map Coloring Problem(地图着色问题)来说明的。

着色问题(Graph coloring, https://en.wikipedia.org/wiki/Graph_coloring)，给定图G有n个顶点，给定k个颜色，问有没有一个方案可以用这k种颜色给这个图的n的顶点着色，使得相邻顶点的颜色不同，时间复杂度 O(2nn) ，是个NP-complete的问题。

用我们现在的计算机的解法有，贪心算法The Welsh-Powell Algorithm，暴力的回溯算法。拿DFS做个说明。

struct Vertex {
    int id;
    bool colored;
    int color;
}

map<int, vector > graph;
int k = colorNum;

// 当前顶点的涂色是否合理
bool isOK(map<int, vector > graph, int id, int color) {
    vector neighbors = graph[id];
    for (vector::iterator it = neighbors.begin(); it != neighbors.end(); ++it) {
        if (colored && it->color == color) {
            return false;
        }
    }
    return true;
}

bool dfs(map<int, vector > graph, int startId, int coloredVertexNum) {
    // graph.size() = n, n is graph’s vertex number
    // 如果涂完了n个顶点，返回true
    if (coloredVertexNum == graph.size()) {
        return true;
    }
    // 否则开始涂色
    else {
        // 遍历尝试k个颜色
        for (int i = 0; i < k; ++i) {
            // 如果当前颜色可行，则涂色
            if (isOK(graph, startId, i)) {
                graph[startId].colored = true;
                graph[startId].color = i;
                vector neighbors = graph[startId];
                // 遍历邻接顶点
                for (vector::iterator it = neighbors.begin(); it != neighbors.end(); ++it) {
                    // 若顶点未着色，则递归
                    if (!it->colored && dfs(graph, it->id, coloredVertexNum + 1)) {
                        return true;
                    }
                }
                // 恢复未涂色状态
                graph[startId].colored = false;
            }
        }
    }
    return false;
}

这个部分用到的图片均来自D-Wave的官方文档。
如果是D-Wave的量子计算机的话，则是另外一种思路。它把图的n的顶点用n个qubit代替，这个qubit就是前面提到的一个量子状态，通过设计一个表达式来描述我们的这个涂色问题，这个表达式叫做Objective，类似机器学习中的损失函数，在机器学习中我们是通过最小化损失函数来得到最优解参数的，这里这个Objective描述的其实是把涂色问题映射成一个量子系统的能量，这个系统的能量最低的状态就对应问题的解。Objective中含有参数，我们解题的过程，就是通过足够小步的调节这些参数，使得这个系统的状态近似处于系统的瞬时基态，最后停止参数的更新，对应的参数就是我们问题的解(具体的运作原理，没看懂，nature上的blog说D-Wave公司自己也说不清楚机器到底是如何运行的，请了个第三方的算法人员具体测了下，用解题的速度从侧面上说明这个芯片的行为像是量子现象的行为)，这个过程也叫量子退火算法(Quantum annealing)。调节参数我们看到的是直接改变数字，其实对应到物理系统中，就是用这些参数去调节温度、电压、电流或磁场等。

那这个涂色问题D-Wave是怎么编程的呢？下面是对D-Wave官方文档(https://www.dwavesys.com/sites/default/files/Map%20Coloring%20WP2.pdf)的一个简述。

如果一个图有2个顶点，给定2种颜色，这个问题的Objective可以表示成

O(a,b;q)=a1q1+a2q2+b12q1q2

其中和是qubit，量子比特，每个量子比特有两种状态0和1，和代表2个顶点，每个顶点的两种可能的取值代表2种颜色，遍历各种可能状态会得到下表

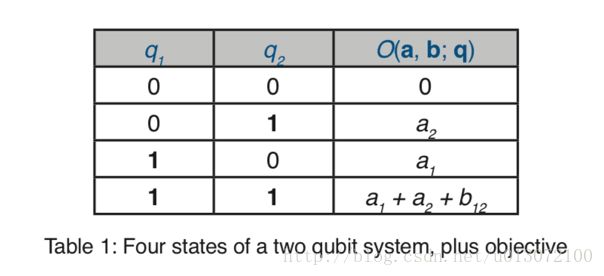
我们知道中间的两种分布是我们涂色方案的解，我们要选择参数 a1 、 a2 和 b12 ，使得 q1 和 q2 取不同的值时，Objective取极小值，暂且不要理会怎么让系统演化到这个状态，我们分析的看一下是否存在这样的参数。

两个顶点在涂色中其实是对称的，意思是 a1 和 a2 应该相等；如果选择这两个参数小于0，则可以满足 q1 和 q2 都为0时的值不会小于其中一个不为0时的值，就会排除掉 q1 和 q2 同时为0的情况，故得到下面的约束

a1=a2<0

如果要排除掉 q1 和 q2 同时为1的情况，我们可以限制(当然你也可以设计其它的限制，比如让下面的和等于1等)

a1+a1+b12=0

这样的话，满足条件的解中的一个为
a1=−1 , a2=−1 , b12=2

量子退火算法的过程就是找到其中的一组或几组合适的参数，使得Objective描述的系统处于ground state(基态)；在测量之前，这个系统是处于叠加态的，就是说 q1 可以是0或1， q2 也可以是0或1，只不过 q1 和 q2 不能取值相同；然后我们去测量这个系统，系统会塌缩到经典物理描述的状态中， q1=1 和 q2=0 或 q1=0 和 q2=1 ，就是我们问题的解。

这种解法的步骤有
具体问题到目标函数Objective的抽象
Objective描述的这种有特定性质的量子系统到物理量子系统的对应
物理量子系统随时间的演化(revolution，含时间的薛定谔方程)，终态的确定
对终态的测量，实现叠加态到确定解的投影

题外话，其实上面Objective描述的这种系统是一个物理中很有名的模型Ising模型的特例，Ising模型的设定很简单，但却很有用，能够解释磁铁的加热后的消磁及冷却后又有磁性的现象(相变)，其它学科也有拿解决一些自己学科的问题。

那如果颜色变多怎么办呢？一个qubit在这里只可以表示两种颜色，可以把多个的qubit组成一个整体，让它可以表示更多的状态，D-Wave是把8个qubit组合在一起，并且qubit之间有耦合(相互作用)，如图

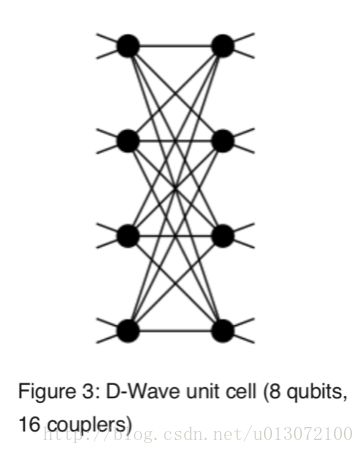
那顶点变多怎么办呢？每个顶点会分配给一个如图的unit cell。

这样一来的话Objective目标函数的描述会比上面提到的多很多变量，不过设计思想还是类似，就是利用unit cell本身的状态以及unit cell之间相互作用。

他们在github有个库(https://github.com/dwavesystems/qbsolv)。

总之，这样架构的量子计算机，只能解决特定类型的问题，不是通用量子计算机。通用量子计算的设计目前还停留在理论层面，科学家们按照我们经典计算机的设计思路，构思了一系列的量子门以及控制单元，然后在这个基础上设计了一系列的量子算法。

5 a flavor of 量子算法

Deutsch Algorithm

问题描述： f 是个二值函数，可以把0和1映射到0和1，f的映射方式就只有4种，用数学方式表示就是

f1:0→0,1→0

f2:0→1,1→1

f3:0→0,1→1

f4:0→1,1→0

这4个函数可以分成两类， f1 和 f2 叫做constant，因为它们的输出和输入无关， f3 和 f4 叫做balanced。现在需要判断给定的 f 是constant还是balanced。经典的做法是，我们需要评估 f 两次才可以判断它是constant还是balanced，这两次是指评估输入为0时的输出和输入为1时的输出。

存在一个量子算法可以值评估 f 一次，就可以断定 f 是constant还是balanced，这个算法就是Deutsch Algorithm。

初始化一个状态为

|ψ0⟩=12(|00⟩−|01⟩+|10⟩−|11⟩)

用 Uf 去作用这个状态，这个操作表示成一个幺正算符(unitary operator)

Uf:|x,y⟩→|x,y⊕f(x)⟩

其中 ⊕ 是加和后再mod2。作用后我们得到

接着我们再用Hadamard gate去作用 |ψ1⟩ 的第一个qubit，第一个qubit是指中 |x,y⟩ 的 x 。然后就会得到

如果 f 是constant的话， |ψ2⟩ 可以化简为

如果 f 是balanced的话， |ψ2⟩ 可以化简为

这样呢，我们就只需要测量的 |ψ2⟩ 第一个qubit的值，就可以确定 f 是constant还是balanced。先不要管各种操作是如何实现的，至少从理论上来说，我们在判定 f 属于哪一类时，只用了一个输入，只评估了一次输出值。

这个虽然是一个很简单的算法，但其处理问题的逻辑和复杂算法是一样的，就是利用一个算符可以同时作用在qubit组成的系统的叠加态的各个分量上，不需要像经典算法那样依次遍历qubit的所有可能组成情况，以此来降低解决问题的时间复杂度。

想了解Deutsch-Jozsa Algorithm, Grover’s Search Algorithm, Quantum Fourier Transform和Shor’s Factorization Algorithm的话，去看QUANTUM COMPUTING From Linear Algebra to Physical Realizations这本书。

6 潘建伟团队2017年在量子计算领域的贡献

在半导体材料中制备出了10个量子比特可以存在和被操作的器件，其中也包含一个超导总线电路，和现在的计算机芯片架构的思路一样，是量子计算机在凝聚态方向架构(原文是solid state platform，我自己一般认为condensed physics和solid state physics差不多，就这么说了)这条道路上的一个进步，可以制备的纠缠态中包含的量子比特越多，计算能力越强大。之前报道的在solid state platform中能够制备的量子纠缠态最多只包含了5个量子比特。

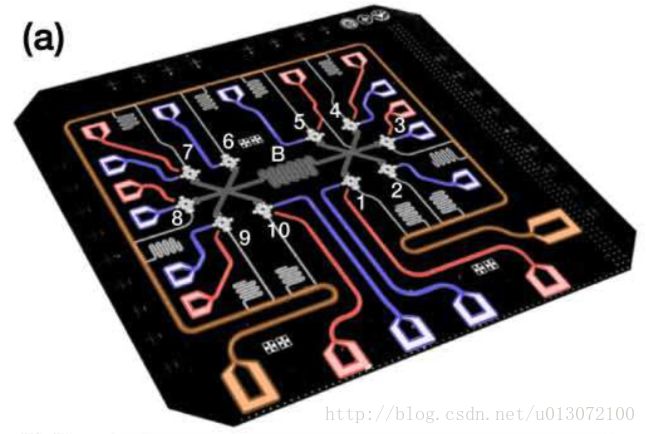
下图是从潘建伟团队2017年的一篇论文的截图，是10个量子比特可以耦合在一起的芯片，图中的1~10可以存放10个量子比特，灰色的线路是超导总线，红色和蓝色是控制线路，橘色是状态读取线路。扭扭曲曲的部分就类似线圈，这种芯片用的是高频交流电，~ GHz。论文就是从实验数据的角度去论证他们确实制备出了这样的10个量子比特纠缠的器件。

实际实验中，核心部件是工作在超低温下的 ~20 mK。

不过芯片的制备材料及fabrication的细节没有看到，只看到写了一些线路是通过吕沉积(aluminum deposition)技术实现的，器件尺寸也没明确看到(也有可能我看漏了)。

7 阿里的施尧耘

http://web.eecs.umich.edu/~shiyy/

了解了下，主要研究是集中在理论量子计算方面，和我原来的研究方向离得较远，就不多说了。潘建伟主要是在实验方向，和我原来的研究方向还相关一些。理论计算方面其实类似于数学，但真正量子计算机的出现还是依赖实验方面的进展，找到稳定的材料和合理的制备工艺。

引进的另一位科学家Mario Szegedy，也主要是从事计算机复杂度理论和理论量子计算的。

阿里如果真正想在商用量子计算机上有所作为，还是应该多些投资在量子计算实验、凝聚态物理、光学等方向。

不过无论哪个方向都是需要科学家们去探索的，平庸的人可以去评价但不应该因盲从而吹嘘，或因短视而诋毁，少跟风媒体多点自己的判断，向致力于前沿科学的研究人员致敬。

ref

http://blogs.nature.com/news/2013/04/further-proof-for-controversial-quantum-computer.html
https://www.dwavesys.com/tutorials/background-reading-series/quantum-computing-primer#h1-0
http://www.nature.com/news/google-and-nasa-snap-up-quantum-computer-1.12999
QUANTUM COMPUTING From Linear Algebra to Physical Realizations
https://arxiv.org/pdf/1304.4595.pdf
https://en.wikipedia.org/wiki/Quantum_annealing
https://www.dwavesys.com/sites/default/files/Map%20Coloring%20WP2.pdf
https://en.wikipedia.org/wiki/Ising_model
https://github.com/dwavesystems/qbsolv
https://baike.baidu.com/item/%E8%AE%A1%E7%AE%97%E6%9C%BA%E4%BD%93%E7%B3%BB%E7%BB%93%E6%9E%84
https://en.wikipedia.org/wiki/CMOS
https://arxiv.org/abs/1310.1339
https://arxiv.org/pdf/1109.3743.pdf
https://www.zhihu.com/question/26933442
https://baike.baidu.com/item/%E9%87%8F%E5%AD%90%E8%AE%A1%E7%AE%97%E6%9C%BA
http://www-reynal.ensea.fr/docs/iq/QC10th.pdf
https://www.zhihu.com/question/22506483
https://arxiv.org/abs/1703.10302