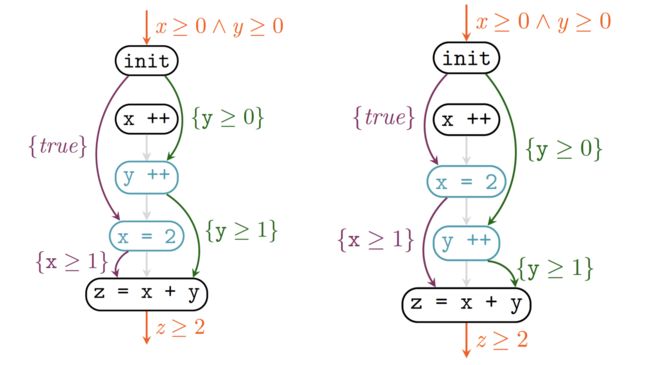Inductive Data Flow Graphs - 基于数据流图的并发程序验证

Inductive Data Flow Graphs

 

# Remark

Conference: POPL 2013

Full Paper: https://www.cs.princeton.edu/~zkincaid/pub/popl13.pdf

 

# Abstract

The correctness of a sequential program can be shown by the annotation of its control flow graph with inductive assertions. We propose inductive data flow graphs, data flow graphs with incorporated inductive assertions, as the basis of an approach to verifying concurrent programs. An inductive data flow graph accounts for a set of dependencies between program actions in interleaved thread executions, and therefore stands as a representation for the set of concurrent program traces that give rise to these dependencies. The approach first constructs an inductive data flow graph and then checks whether all program traces are represented. The size of the inductive data flow graph is polynomial in the number of data dependencies (in a sense that can be made formal); it does not grow exponentially in the number of threads unless the data dependencies do. The approach shifts the burden of the exponential explosion towards the check whether all program traces are represented, i.e., to a combinatorial problem (over finite graphs).

 

# Introduction

这篇文章借鉴了model checking方面的一些技术，对并发程序做验证。即给定一个并发程序P，一组pre-condiction和post-condiction，证明从pre-condiction出发执行P可以推断出post-condiction。

 

本文工作背后的一个动机是，对于并发程序来说，是否可以将针对顺序的静态分析技术与模型检测技术结合起来。目前将静态分析扩展到并发控制或将模型检查扩展到一般数据域的方法已经取得了相当大的进展。每一种方法都提供了不同的视角来规避一个相同的基本问题：“证明并发程序正确性所需的空间随着线程数呈指数增长”。为了解决这个问题，作者提出了Inductive Data Flow Graphs (idfg)，即包含归纳断言的数据流图，作为验证并发程序的基础。

 

# Example

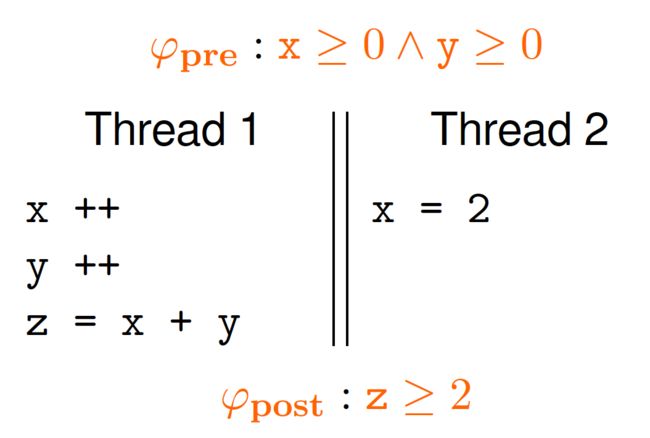
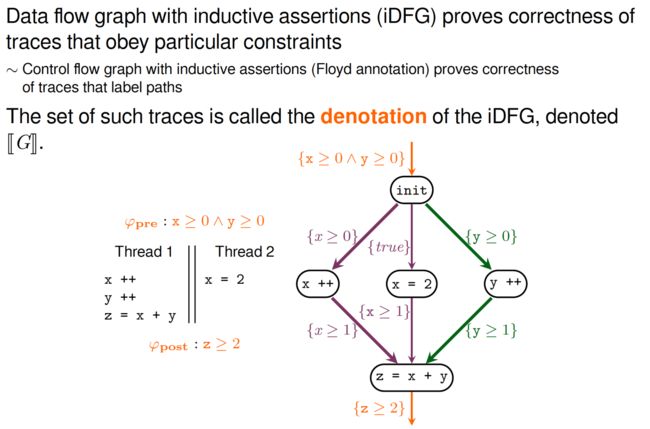
考虑下图这个例子，假设初始条件是x>=0和y>=0，我们能证明这个并发程序执行后一定满足z>=2吗？实际上并发程序的特点就是有线程交错，就是每一条语句执行完后可能会跳到其它线程去。

 

这个程序的执行顺序有很多种可能性，如下所示。实际上线程交错的可能性是随着线程的数量是呈指数增长的，每一种执行可能性都去证明它是对的话空间开销特别大，存在状态爆炸的问题。

//E1: x=2； x++； y++； z=x+y; //E2: x++； x=2； y++； z=x+y; //E3: x++； y++； x=2； z=x+y; //E4: x++； y++； z=x+y; x=2；

 

以E2为例，要证明在E2这条执行轨迹上是正确的，只需要使用Hoare逻辑一步步推理即可，如下图所示。在z=x+y执行之前，我们可以得知x>=1并且y>=1，因此z>=2。

 

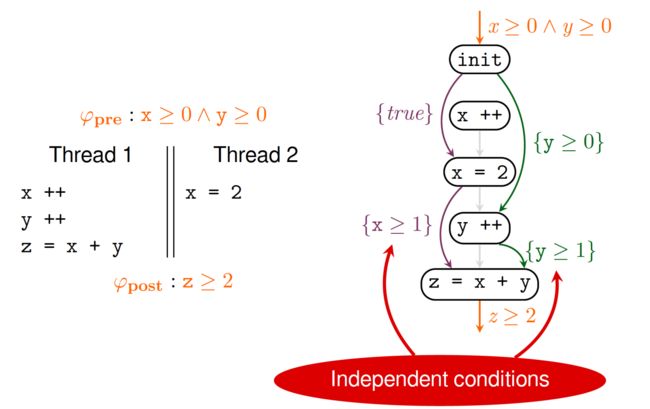
从数据流的角度，这个证明可以进一步简化，我们们可以单独证明在z=x+y执行之前，x>=1; 单独证明在z=x+y执行之前，y>=1。如下图所示，这样的好处是证明x>=1的时候，我只关心与x变量相关的数据流，而证明y>=1的时候，我只关心与y变量相关的数据流。这样单独证明一个断言的开销很小，并且这两个证明互不影响（可以并行）。

 

 

现在我们再来看看E2和E3这两种情况有什么相似之处？如下图所示，是不是x=2和y++这两条语句的执行顺序对这个程序的结果没有影响，证明方式也是一模一样。

 

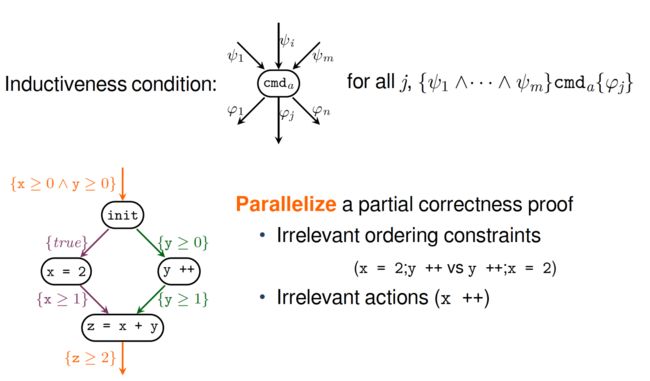
由此，我们引入Inductive Data Flow Graphs (iDFG)的概念。iDFG说明了交错线程执行中数据操作之间的一组依赖关系，因此代表了产生这些依赖关系的并发程序跟踪集。该方法首先构造一个iDFG，然后检查是否表示了所有程序跟踪。iDFG的大小在数据依赖项的数量上是多项式的（在某种意义上可以称为形式化的）；它不会在线程的数量上呈指数增长，除非数据依赖项这样做。直观地说，这种简洁性是可能的，因为iDFGs只表示程序的数据流，并且抽象出与证明无关的控制特性。该方法将指数爆炸的负担转移到检查是否所有程序轨迹都被表示上，这是一个组合问题（在有限图上）。

 

# Approach

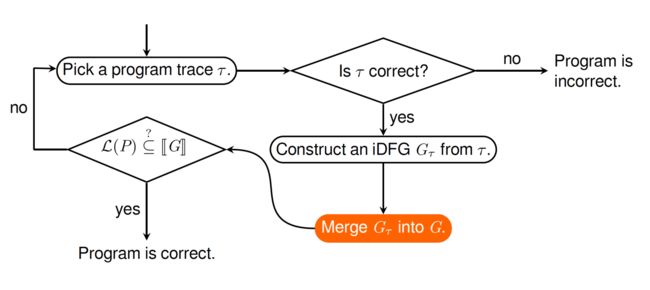
这篇文章的验证思路跟Ultimate Automizer是一样的，本质上就是找一个自动机包含住所有可能的error trace，只要能证明这个自动机没错，就说明这个程序没错。本文的主要验证流程如下图所示，取一条程序trace，判断这条trace是否正确，如果trace不正确，那么找到了一个反例，算法终止；否则为这条trace构造iDFG，然后下一条trace又构造新的iDFG，然后合并iDFG直到合并后的iDFG覆盖了所有可能的trace（这就是CEGAR方法）。

 

而给trace构造iDFG实际上就是把很多线程交错的情况合并了。前面解释了，用iDFG同样也能证明trace的正确性。 所以剩下的问题就是：

• Q1：怎么根据trace生成iDFG？

• Q2：怎么合并iDFG？

• Q3：怎么判断合并后的iDFG能包含住程序P？

 

（这也是文章的主要算法内容，以后有空再写）

 

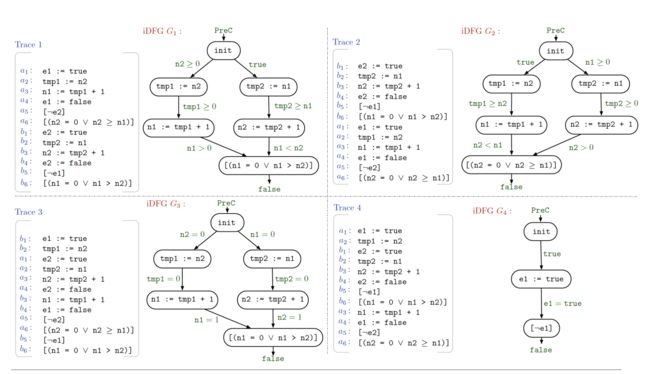
# Another Example