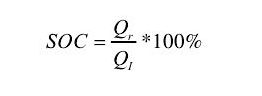电量(SOC)算法
除了参数的监控与保护之外,作为BMS系统,其中最重要的功能还有一项,那便是SOC的计算。
SOC,全称是State of Charge,系统荷电状态,也叫剩余电量,代表的是电池使用一段时间或长期搁置不用后的剩余容量与其完全充电状态的容量的比值,常用百分数表示。
其取值范围为0~100,当SOC=0时表示电池放电完全,当SOC=100时表示电池完全充满。
那么SOC有什么意义呢?
任何一个产品,对于一般的终端用户而言,如果对其直接提供电压、电流之类的电池参数,那么用户可能十分费解,因为对他们来说,使用的电源产品唯一能够理解的,似乎就只有电量。
比如当我询问你的手机还剩多少电?你肯定不会回答电池的端电压还有3.54V,而是直接告诉我还剩大概80%。电动车也是一样,我们甚至可以粗糙的用几个柱状图来表示电池当前的状况,这样也总比直接提供准确的电压要好理解很多,即使不准,但能让用户直观的理解工程师想要表达的意思。
因此,计算出准确的SOC,不仅能提升用户体验,而且好能延长产品的使用寿命,这对于任何一块产品而言意义都非常巨大。
在一般的BMS系统中,计算电量的方式大概有两种:
①:硬件
所谓硬件,便是使用一些专门的电量计芯片来计算电量,比如说TI的BQ34Z100,这是一块基于阻抗跟踪技术的电量计,其计算精度不错,而且操作简单,只需要在前期进行一些简单的操作(使用TI官方软件进行基本参数配置,计算电池化学参数CHEM_ID,进行充放电循环学习导出量产文件等)然后就可以直接从芯片里读出电量值。(电量计芯片的方法本文不涉及,感兴趣的同学可以自行查阅资料,或者在本文下留邮箱)
②:软件
软件计算SOC的方法也不少,有开路电压法、安时积分法、内阻法、神经网络和卡尔曼滤波法……
开路电压法由于要预计开路电压,因此需要长时间静置电池组,内阻法存在着估算内阻的困难,在硬件上也难以实现,神经网络和卡尔曼滤波法则由于系统设置的困难,而且在电池管理系统中应用时成本很高,不具备优势,因此相对于开路电压法、内阻法、神经网络和卡尔曼滤波法本而言,安时积分由于简单、有效而常被采用。
本文主要介绍基于STM32的BMS的SOC的编程语言算法。
----------------------------------------------------------------------------------------------
积分是一个数学模拟的概念,如果转化为生活语言,就是累积一端时间的量,如果转化为程序语言,就是把某个变量相乘在相加计算和。
安时积分中的基本参量自然是电流,在任何一个能源系统运行之时,最能够体现其运行负荷状态的必然就是电流,比如一个电机,如果想要转的快,回路上的电流必然增大,比如一个灯泡,如果想要更亮更闪,回路上的电流也要增大。
SOC的数学定义是什么?
上面说过,SOC就是一颗电池还剩多少电,也就是容量,电池容量的定义是,在一定条件下,所放出的电量,即电池的容量,我们通常以安培、小时作为单位,简称安时(用 AH 表示)。
假如有一颗电池当前的容量是20AH,就是说明,如果我们用1A的电流来进行放电,理论上它可以使用20个小时,等我们把这颗电池用光之后,再使用1A的电流来充电,理论上也需要20个小时才能充满。
如果使用2A的电流来充放电,那么时间也会从20小时缩短到10小时……
安时积分的基本原理就是把电流按照时间进行累计,然后记入剩余电量之中,这和用管子朝泳池里灌水是一个道理。
系统启动,传感器开始电流采集,假如每隔20us采集一次,如果采集到的充电电流是1.5A,那么我就认为,在这20us的时间段内,充电电流一直都是1.5A,那么这段时间里增加的电量就是1.5A * 20us(这里为了表达清晰暂时不转换单位)。
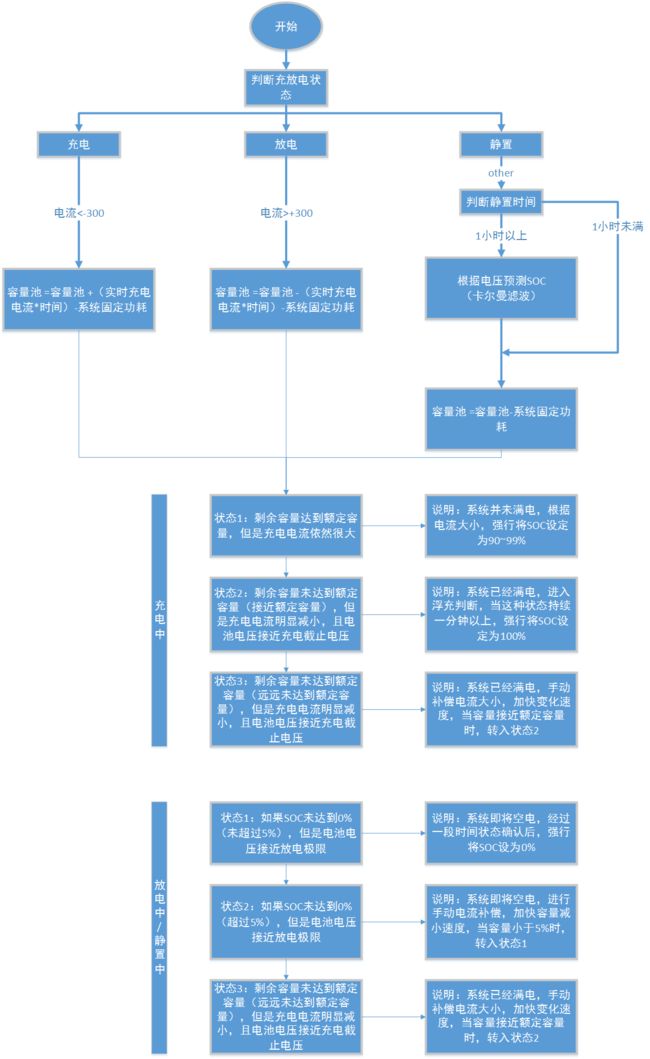
系统充电:现在的剩余电量 = 20us前的电量 + 20us内产生的电量;
系统放电:现在的剩余电量 = 20us前的电量 - 20us内产生的电量;
我们采集到的电流信息,是负载/充电器回路上的电流信息,当电流大于某个阈值的时候(300mA),我们认为是充电,当电流小于某个阈值的时候(-300mA),我们认为是放电,这个没有问题,不过,如果采集到的电流为0,那么系统就真的没有任何消耗吗?
当然不是,就算是MCU本身也是需要消耗能源的,它使用的也是电池的电,只不过没有计入积分之中,如果想要算法更加精确,我认为BMS板子的固定功耗是不能忽略的,虽然电流消耗不大,但毕竟是时时刻刻的在消耗,而且这个消耗几乎不会有很大的改变,如果考虑了固定功耗,那么新的算法如下:
系统充电:现在的剩余电量 = 20us前的电量 + 20us内产生的电量 - 系统固定功耗电流;
系统放电:现在的剩余电量 = 20us前的电量 - 20us内产生的电量 - 系统固定功耗电流;
tim_cal_ms = OSTimeGet() - time;//就算现在经过的时间 time = OSTimeGet(); //保存现在的时间 /* 安时积分 */ /* 容量 = (当前功率电流 - 系统固定功耗) * 时间 */ cap_mAms = (cap_mAms - (current_mA * tim_cal_ms)) - (SYSTEM_FIXED_POWER_CURRENT * tim_cal); /* 充电电量或者放电电量累积超过 10mAh */ if((cap_mAms > 36000000) || (cap_mAms < -36000000)) { capacity += cap_mAms / 3600000; /*整数个 mAh */ cap_mAms = cap_mAms % 3600000; /* 不足1mAh的电量,做累积 */ }
以上便是安时积分的基本原理,看着非常简单,不过,现在还有一个问题,20us内产生的电量(current_mA * tim_cal_ms)这个值我是可以计算出来的,但是20us前的电量(cap_mAms)这个值又从何而来呢?
这个自然是来自20us之前的状态,我们再往前推,找到40us前的状态,然后再往前推,找到60us之前的状态……
如果一直往前推以后,肯定会发现一个问题,这个电量算法的安时积分需要一个起点,也就是系统运行之后,我的第一个参与计算的电量是多少?
初始电量的来源一般采用开路电压法来确认,一颗新电池,如果在静态的情况下(无充放电)呆了2个小时以上,那么这个时候直接使用电压来寻找电量是很准确的,比如说3.6V对应100%电量,2.7V对应1%电量,3V对应50%电量,这完全可以做几次充放电实验来列出一个表,横坐标是电压,纵坐标就是电量。
1 const OCV_VALUE_S OcvTable_Dischg_1C[101] = { {2999, 0}, 2 {3129, 1}, {3262, 2}, {3292, 3}, {3314, 4}, {3330, 5}, 3 {3344, 6}, {3366, 7}, {3375, 8}, {3383, 9}, {3390, 10}, 4 {3404, 11}, {3410, 12}, {3416, 13}, {3421, 14}, {3426, 15}, 5 {3437, 16}, {3441, 17}, {3446, 18}, {3450, 19}, {3454, 20}, 6 {3462, 21}, {3466, 22}, {3470, 23}, {3473, 24}, {3480, 25}, 7 {3484, 26}, {3487, 27}, {3490, 28}, {3493, 29}, {3497, 30}, 8 {3503, 31}, {3506, 32}, {3510, 33}, {3513, 34}, {3519, 35}, 9 {3523, 36}, {3526, 37}, {3529, 38}, {3532, 39}, {3539, 40}, 10 {3543, 41}, {3546, 42}, {3550, 43}, {3554, 44}, {3561, 45}, 11 {3565, 46}, {3569, 47}, {3573, 48}, {3578, 49}, {3587, 50}, 12 {3592, 51}, {3596, 52}, {3601, 53}, {3607, 54}, {3617, 55}, 13 {3623, 56}, {3629, 57}, {3635, 58}, {3641, 59}, {3654, 60}, 14 {3661, 61}, {3667, 62}, {3674, 63}, {3688, 64}, {3696, 65}, 15 {3703, 66}, {3710, 67}, {3718, 68}, {3726, 69}, {3741, 70}, 16 {3749, 71}, {3758, 72}, {3766, 73}, {3782, 74}, {3790, 75}, 17 {3799, 76}, {3807, 77}, {3816, 78}, {3833, 79}, {3842, 80}, 18 {3851, 81}, {3860, 82}, {3877, 83}, {3887, 84}, {3896, 85}, 19 {3905, 86}, {3914, 87}, {3933, 88}, {3943, 89}, {3953, 90}, 20 {3962, 91}, {3972, 92}, {3992, 93}, {4002, 94}, {4013, 95}, 21 {4024, 96}, {4048, 97}, {4063, 98}, {4082, 99}, {4190, 100}};
系统上电以后,读取电池总电压,然后寻找到一个初始的电量值,虽然有些误差,不过完全可以用这个值来参与以后的积分运算……
不过,还有一个问题,如果这块电池并未静置2小时以上,刚才还在大功率放电,然后由于某种问题系统重启,这个时候采用开路电压法似乎就不可行了!
关于这个问题,可以用一些设计来解决,比如MCU不断电,或者设计一颗外部独立RTC,增加外部的flash,实时储存SOC和相关的信息,在系统启动后,读取flash中的SOC,然后判断其存入的时刻是否经过了2小时,如果上一次存入的SOC的时间和现在的时间相差2小时,那么可以采用开路电压法确定初始SOC。如果事件间隔很小,那么就直接使用FLASH中存储的SOC值来当做初始SOC。
----------------------------------------------------------------------------------------------------------------
用安时积分算法来计算SOC,其最大的缺点就是误差容易累积,甚至有些误差是不可避免的,比如采用开路电压法得到的初始SOC值,比如硬件的采集精度,如果每次实际的充电电流是0.9A,而采集出来的电流是0.1A,按照时间长此以往的累积下去,最后的电量肯定是虚高的。
在这个时候,我们需要一些方法,利用电池本身的特性,来对安时积分算法进行校准。
在循环中校准
锂电池充电需要经过几个过程,当电池电量低,那么首先是恒流升压充电,这时电流固定不变,电压逐渐升高,等电池电量接近饱和之时,会变成恒压降流充电,电压不在发生明显变化,电流会急速减小,过程如下图所示。
正是因为锂电池的如此特性,因此我们便有了一个校准SOC的时机,当在充电过程中,一旦出现了恒压降流,并且这种状态持续了足够长的时间,那么就可以说明电池已经充满了。
假如由于之前的计算和采集存在误差,导致系统现在的SOC等于70%,系统也可以主动使用算法来修正这个结果,要么直接将SOC人工设定为100%,要么主动放大积分的因子,使其加速充电,以更快的速度朝着100%毕竟。
在放电过程中也可以校准,当电池的电压已经接近低压极限,然后电流也只有几百个毫安,那么就可以将SOC看做是0%了。
卡尔曼滤波和开路电压校准
前面提到过,当电池静置2小时以后,此刻电压相对平稳,我们可以使用开路电压法直接估算SOC的最新值,也可以用开路电压和卡尔曼滤波结合起来用。
卡尔曼滤波是一种很有名的数据校准算法,也可以应用在SOC的计算之上。
卡尔曼滤波的本质是解决一个信任度的问题,我们采集到的电压查表得到的SOC,与安时积分计算出来的SOC,到底哪个更加准确?
具体的算法理论这里不展开,我直接把自己的代码贴出来以供参考:
uint8_t Kalman_Filter_Algorithm(float calculation_vaule, float Q, float R, float measure_vaule) { static float x_last = 0; static float p_last = 0; static float kg; static float x_mid; static float x_now; static float p_mid; static float p_now; /* Q:过程噪声,Q增大,动态响应变快,收敛稳定性变坏 R:测量噪声,R增大,动态响应变慢,收敛稳定性变好 */ if ((measure_vaule > calculation_vaule) && ((measure_vaule - calculation_vaule) > 10)) { measure_vaule = calculation_vaule + 10; } else if ((calculation_vaule > measure_vaule) && ((calculation_vaule - measure_vaule) > 10)) { measure_vaule = calculation_vaule - 10; } else { ; } x_now = calculation_vaule; // 先验估算值 x_mid = calculation_vaule; // 先验协方差 p_mid = p_last + Q; // 卡尔曼增益 kg = p_mid / (p_mid + R); // 最优估计值 x_now = x_mid + kg*(measure_vaule - x_mid); // 最新协方差 p_now = (1 - kg)*p_mid; p_last = p_now; x_last = x_now; return (uint8_t)x_now; }
有了以上量准校准的方法,相信系统的SOC在一般情况下不会偏差太大。
现在做个总结,关于SOC的计算策略图如下: