重新研读fish千聊课04

import scipy.stats
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%config InlindomneBackend.figure_format ='retina'

计算机模拟

生成随机数

np.random.seed(5)

疑惑：为什么要有种子呢？

np.random.random(5)

array([ 0.22199317,  0.87073231,  0.20671916,  0.91861091,  0.48841119])

np.random.randint(0,9,10)

array([0, 4, 4, 3, 2, 4, 6, 3, 3, 2])

num =10000
x = np.random.random(num)
y = np.random.random(num)

pi = np.sum(x**2+y**2<1)/num*4
print ("π=",pi)
  π= 3.1756

小疑惑，random()生成的随机数，是默认为0-1之间的吗？
-- 刚才试着将结果打印出来了，确实是0-1之间的数字，没有大于1的随机数

我将num设置到1亿，结果电脑直接卡机了，强制关机后才缓过来。

疑问。x²+y²＜ 1，这个结果是数量吗？总觉得应该用counts（）方法，而非sum（）方法啊

--原来x²+y²＜ 1结果是一堆布尔型的结果，而sum是不是只是把为true的结果进行相加了，ture又是1的意思。

x**2+y**2<1

array([ True,  True,  True, ...,  True,  True,  True], dtype=bool)

num*4

接下来，还可以画图，我们来试试吧

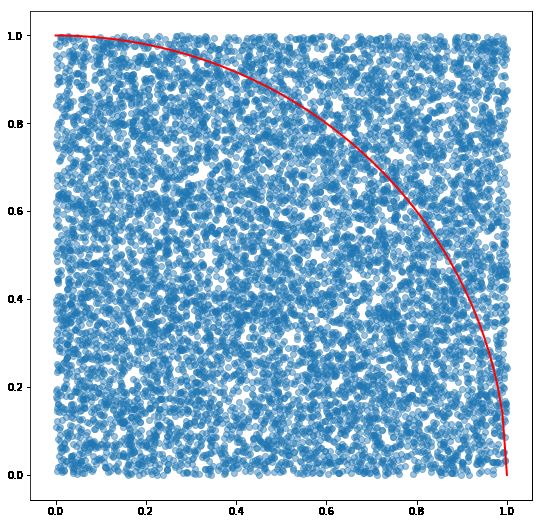
plt.figure(figsize=(9,9))

plt.scatter(x,y,alpha=0.45)

x2 = np.arange(0,1.01,0.01)
y2 = np.sqrt(1-x2**2)
plt.plot(x2,y2,'r',lw=2)
#plt.plot(x2, y2, 'm', lw=3)
plt.show()

新增知识点：

圆半径为1的情况下，如何计算另外两条直角边。 1-x²=y²。y=sqrt（1-x²）
sum（）一个过滤函数，是将布尔型结果中的true，计数求和。如：np.sum(x2+y2<1)

错误记录：

. 拼写错误，arange，我多写了一个r，arrange。

output_10_0.png

np.arange(0, 1.01, 0.01)

array([ 0.  ,  0.01,  0.02,  0.03,  0.04,  0.05,  0.06,  0.07,  0.08,
        0.09,  0.1 ,  0.11,  0.12,  0.13,  0.14,  0.15,  0.16,  0.17,
        0.18,  0.19,  0.2 ,  0.21,  0.22,  0.23,  0.24,  0.25,  0.26,
        0.27,  0.28,  0.29,  0.3 ,  0.31,  0.32,  0.33,  0.34,  0.35,
        0.36,  0.37,  0.38,  0.39,  0.4 ,  0.41,  0.42,  0.43,  0.44,
        0.45,  0.46,  0.47,  0.48,  0.49,  0.5 ,  0.51,  0.52,  0.53,
        0.54,  0.55,  0.56,  0.57,  0.58,  0.59,  0.6 ,  0.61,  0.62,
        0.63,  0.64,  0.65,  0.66,  0.67,  0.68,  0.69,  0.7 ,  0.71,
        0.72,  0.73,  0.74,  0.75,  0.76,  0.77,  0.78,  0.79,  0.8 ,
        0.81,  0.82,  0.83,  0.84,  0.85,  0.86,  0.87,  0.88,  0.89,
        0.9 ,  0.91,  0.92,  0.93,  0.94,  0.95,  0.96,  0.97,  0.98,
        0.99,  1.  ])

个人理解：测试一下arange方法的作用。np.arange(x,y,d)是按照顺序生成x-y区间的数字，单位是d，也称作间隔为d。

连续分布--正态分布

模拟面包重量的分布

mean = 950
std = 50

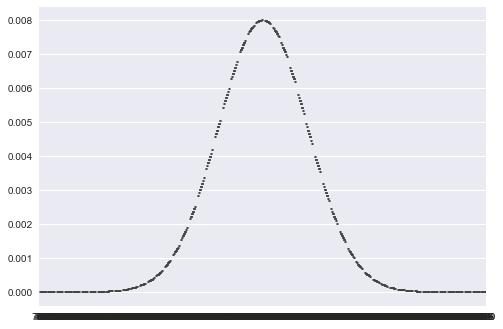
# 生成满足正态分布的随机数，并绘制直方图
sample = np.random.normal(mean, std, size=365)
plt.hist(sample, bins=30, alpha=0.7, rwidth=0.9, normed=True)

plt.show()

output_14_0.png

mean= 950
std = 50

sample = np.random.normal(mean,std,size=365)
plt.hist(sample,bins = 30,rwidth=0.9,normed=True)
plt.show()

错误记录：

(mean,std,size=365)中的逗号，我写作了.。一直报错，都没发现原因，有点傻啊

output_15_0.png

用scipy.stats也可以生成正太分布哦

mean = 950
std = 50

bom =scipy.stats.norm(mean,std)

错误记录

scipy中正态分布方法，只是简写成norm。 scipy.stats.norm 而我写成额normal

x = np.arange(700,1200,1)
y = bom.pdf(x)
plt.plot(x,y)
plt.show()

output_19_0.png

我在这里尝试在notebook中安装seaborn，然后成功了。哈哈哈

!pip install seaborn

Requirement already satisfied: seaborn in d:\programdata\anaconda3\lib\site-packages

import seaborn as sns
sns.boxplot(x,y)
sns.plt.show()

output_21_0.png

自己强行胡乱尝试用seaborn画图，结果捣鼓出来一个。

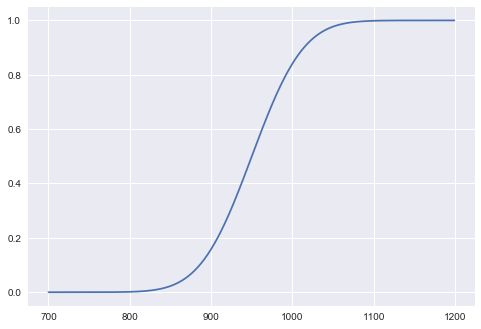
# 接下来画概率累计函数
x = np.arange(700,1200,1)
#y = np.norm.cdf(x)
y = bom.cdf(x)
plt.plot(x,y)
plt.show()

错误记录：

norm.cdf被我写作为np.norm.cdf。其实这个norm是个自定义变量啊

output_23_0.png

计算买到的面包小于1000克的概率

这个该怎么计算呢？有套路吗？

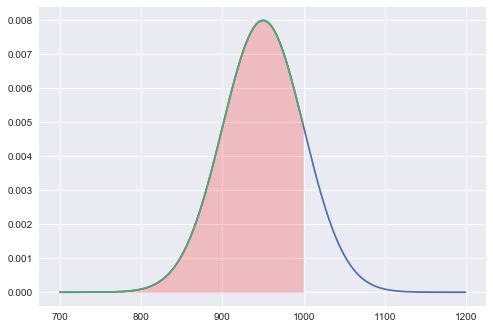
先画出概率密度函数的曲线
x = np.arange(700,1200,1)
y = bom.pdf(x)
plt.plot(x,y)


plt.vlines =(1000,0,bom.pdf(1000))

>  ？？？我的这段代码里，为什么plt.vlines()方法没有反应呢？
 
x2 = np.arange(700,1000,1)
y2 = bom.pdf(x2)
plt.plot(x2,y2)

plt.fill_between(x2,y2,color= 'red',alpha=0.2)


plt.show()

错误记录：
1.plt.fill_between()我写的是fillbetween，竟然没有加下划线。

plt.fill_between()内部的参数，不仅仅应该是x轴，应该xy轴，而我的参数设定只有700,1000，这是只基于x轴的思路。
plt中的颜色设定都是color=“”的形式，而是采用的简写实在不科学。

概念混淆。 pdf和cdf完全混淆了。所以我的显示完全是两张图。我x，y的函数用的是pdf，而x2，y2，用的是cdf函数，所以总共觉得图形不对。
疑惑，为甚么我的图形，没有完整显示呢？-- 因为plt.vilines没起作用

output_25_0.png

红色区域的面积，就是700-1000g的概率和。那么概率和，就应该用概率累计函数。

print("面包等于1000g的概率是：",bom.pdf(1000))
print("小于1000g的概率是：",bom.cdf(1000))

面包等于1000g的概率是： 0.00483941449038
小于1000g的概率是： 0.841344746069

回到刚才的自我提问，小于1000g的概率，有套路吗？
有！
小于1000g的概率，就是求700g的概率+701g的概率+.......+999g的概率，也就是概率累计和嘛。直接求cdf（1000）即可。

求面包大于1000g的概率

这下简单了，就是求1000g的概率加到1200g的概率嘛，用整体减去700到1000g的概率和，就可以了呀。
整体等于1，那就好办啦。

print('面包大于1000g的概率是：',1-bom.cdf(1000))

面包大于1000g的概率是： 0.158655253931

print('面包大于1000g的概率是：',bom.sf(1000))
##错误记录：计划求反函数，谁知记错了方法名，应该用sf，而非isf

面包大于1000g的概率是： 0.158655253931

刚才搜到了几个方法的解释，常用的概率函数主要可以概括为以下几类：

根据变量求小于变量的概率(cdf)

根据变量求大于变量的概率(sf)

根据概率求相应的小于变量(ppf)

根据概率求相应的大于变量(isf)

接着做题

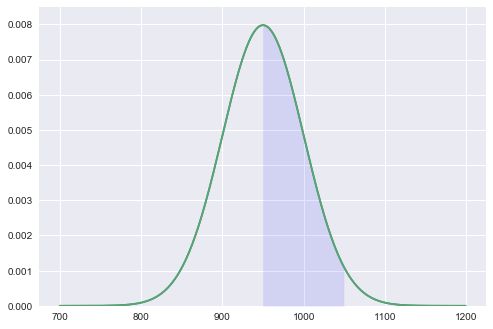
计算买到的面包处于950到1050范围内的概率

## 这种情况下，直接用cdf（1050）-cdf（950）就可以啊
#绘制PDF曲线
x = np.arange(700, 1200, 1)
y = norm.pdf(x)
plt.plot(x, y)

#绘制竖线
#plt.vlines(950, 0, norm.pdf(950))
#plt.vlines(1050, 0, norm.pdf(1050))

#填充颜色
x2 = np.arange(950, 1050, 1)
y2 = norm.pdf(x2)
plt.fill_between(x2, y2, color='blue', alpha=0.1)

#设置y轴范围
plt.ylim(0,0.0085)

plt.show()
print('面包950-1000g之间的概率是：',bom.cdf(1050)-bom.cdf(950))

output_34_0.png

面包950-1000g之间的概率是： 0.477249868052

90%的情况下，买到的面包是小于多少克的？

根据概率求相应的小于变量(ppf)

这就是典型的用概率求变量。已知概率，求小于变量，该怎么算呢。小于1000g的概率，是用概率累计函数cdf，即cdf（1000）

已知概率，求变量则应该是cdf的反函数ppf.

先看看概率累计函数吧

x = np.arange(700, 1200, 1)
y = norm.cdf(x)
plt.plot(x, y)
plt.show()

output_36_0.png

print('90%的时候面包小于：',bom.ppf(0.9))

90%的时候面包小于： 1014.07757828

80%的情况下，买到的面包是大于多少克的？

根据概率求相应的大于变量(isf)

这种时候，就该用sf（survival function）的反函数isf（inverse survival function）。

print ('80%的时候面包大于:',bom.isf(0.8),'g')

80%的时候面包大于: 907.918938321 g

离散分布 - 二项分布

投硬币问题模拟

outcome =np.random.randint(0,2,10)
#outcome= list(outcome)

np.sum(outcome)

哦哦，明白啦，布尔型数据是0和1，然后用sum求和方式来计算，能够参与计算的只有1啊，就变相的数了有多少个1，好高明啊

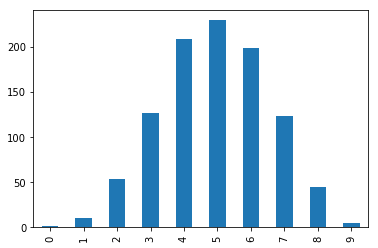
sample=[np.sum(np.random.randint(0,2,10))for i in range(1000)]
# 随机生成10个，0-2之间的整数（其实就是0,1），然后重复这个动作1000次，则会生成1000组10个数组

sample= pd.Series(sample)
sample

0      7
1      4
2      4
3      6
4      6
5      5
6      6
7      4
8      5
9      4
10     4
11     4
12     7
13     5
14     4
15     6
16     1
17     6
18     4
19     8
20     6
21     3
22     6
23     7
24     7
25     7
26     2
27     4
28     2
29     4
      ..
970    5
971    4
972    6
973    4
974    5
975    5
976    4
977    4
978    7
979    1
980    3
981    4
982    4
983    7
984    6
985    3
986    5
987    4
988    5
989    4
990    6
991    3
992    4
993    5
994    3
995    6
996    5
997    9
998    3
999    4
Length: 1000, dtype: int64

#sample.value_counts().plot.bar()
#sample.value_counts().sort_index().plot.bar()
#plt.show()
##错误记录，sample还需要数组化（相当于列表化），但我没数组化后赋值给sample，使得已知报错，无法运算

sample.value_counts().sort_index().plot.bar()
plt.show()

output_46_0.png

投硬币问题的二项分布

n = 10
p = 0.4

mean_bionom = n*p
std_bionom =n*p*(1-p)
print(n*p,n*p*(1-p))

binomial = scipy.stats.binom(n,p)
print (binomial)

4.0 2.4

x = np.arange(0,11,1)
y = binomial.pmf(x)
plt.plot(x,y)
plt.vlines(x,0,y,colors='b')
##疑惑：为什么这里要写0
plt.show()

错误记录： 1.写y值时，我总是要用np.binom.pmf(x),要加上np前缀，但实际上上，data.pmf（x）就可以啦。
---------------------------------------------------------------------------

TypeError                                 Traceback (most recent call last)

 in ()
      3 plt.plot(x,y)
      4 #plt.vlines(x,0,y,colors='b')
----> 5 plt.vlines(x, 0, binomial.pmf(x), colors='b')
      6 ##疑惑：为什么这里要写0
      7 plt.show()


TypeError: 'tuple' object is not callable

x = np.arange(0,11)
plt.plot(x, binomial.pmf(x), 'bo')
plt.vlines(x, 0, binomial.pmf(x), colors='b')
plt.ylim(0,0.3)
plt.show()

---------------------------------------------------------------------------

TypeError                                 Traceback (most recent call last)

 in ()
      1 x = np.arange(0,11)
      2 plt.plot(x, binomial.pmf(x), 'bo')
----> 3 plt.vlines(x, 0, binomial.pmf(x), colors='b')
      4 plt.ylim(0,0.3)
      5 plt.show()


TypeError: 'tuple' object is not callable

mean,var =binomial.stats()
print(binomial.stats())

(array(4.0), array(2.4))

应用

某家风投企业，投资成功的概率是5%，如果它投了100个项目，恰好有5个成功的概率是多少？

n = 100
p = 0.05
binom = scipy.stats.binom(n,p)
print(binom)

##恰好成功5个，就是求5的对应概率，就是pmf
binom.pmf(5)

0.18001782727043672

投资至少成功了5个的概率？

#至少成功5个，就是大于等于5
1-binom.cdf(4)

0.56401869931428927

binom.sf(4)

0.56401869931429105

10%的情况下，至少能成功几个？

#这也是一个大于等于的情况，用生存函数
binom.isf(0.1)

8.0

离散分布 - 泊松分布

有一家便利店使用泊松分布来估计周五晚上到店买东西的顾客数，根据以往数据，周五晚上平均每个小时的顾客数是20。

lmd = 20
poisson = scipy.stats.poisson(lmd)
#错误记录： poisson 被我拼写为poission。 读了个i

x = np.arange(0,40)
plt.plot(x, poisson.pmf(x), 'bo')
#plt.vlines(x, 0, poisson.pmf(x), colors='b')
#plt.ylim(0,0.1)
plt.show()

output_63_0.png

mean,var= poisson.stats()
print('mean=',mean,'var=',var)

mean= 20.0 var= 20.0

#顾客数恰好为20的概率
poisson.pmf(20)

0.088835317392084806

#顾客数小于等于15
poisson.cdf(15)

0.1565131346397429

#顾客数大于等于20
poisson.sf(19)

错误记录：

大于等于20，就是包含20，那么久该从19之后算起，如果我输入20，则是从20之后开始计算。应该是19

疑惑

不过什么时候该用20，什么时候该用19呢，难道是大于的时候吗？为什么小于等于15，就使用cdf（15），而大于等于20就使用sf（19）呢？

0.44090741576867482

poisson.ppf(0.9)

26.0

基本作业

机票超卖现象

假设某国际航班有300个座位，乘客平均误机率是2%。

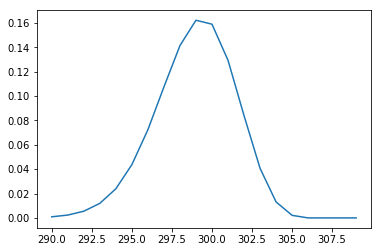
1、如果一共卖出305张机票，那么登机时人数超额的概率是多少？

n = 305
p=0.98
binomial = scipy.stats.binom(n,p)

plt.plot(np.arange(290,310,1),binomial.pmf(np.arange(290,310,1)))
plt.show()

output_70_0.png

## 超额的概率，就是实际人数超过300的概率. 此时n=305
#应该计算大于等于301的情况，sf函数
print ('超员的概率为：',binomial.sf(300))

超员的概率为： 0.269150138198

2、如果一共卖出305张机票，登机时最多只超额1人的概率是多少？

#只超额1人，就是小于等于301嘛。 应该使用cdf

print ('只超额1人的概率：',binomial.cdf(301))

只超额1人的概率： 0.860144501066

3、一共卖几张票，可以保证不超额的概率至少是90%。

n1 = 309
bm1=scipy.stats.binom(n1,p)

x*0.9<300

array([ True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True], dtype=bool)

bm1.isf(0.9)

300.0

重新研读fish千聊课04

计算机模拟

生成随机数

连续分布--正态分布

模拟面包重量的分布

求面包大于1000g的概率

刚才搜到了几个方法的解释，常用的概率函数主要可以概括为以下几类：

接着做题

90%的情况下，买到的面包是小于多少克的？

80%的情况下，买到的面包是大于多少克的？

离散分布 - 二项分布

投硬币问题模拟

投硬币问题的二项分布

应用

离散分布 - 泊松分布

基本作业

你可能感兴趣的:(重新研读fish千聊课04)