Boston_House_Price经典例子分析

最近学习了线性回归，然后拿经典数据集来练习。
数据集大小为[506,13],一共506个样本，13个特征([‘CRIM’ ‘ZN’ ‘INDUS’ ‘CHAS’ ‘NOX’ ‘RM’ ‘AGE’ ‘DIS’ ‘RAD’ ‘TAX’ ‘PTRATIO’ ‘B’ ‘LSTAT’])，target大小为[506，1]
可以先通过matplotlib来直观感受这些特征分别与房价的关系。



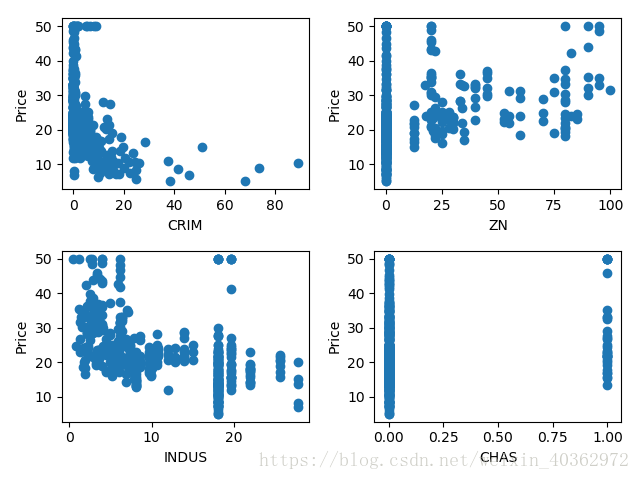
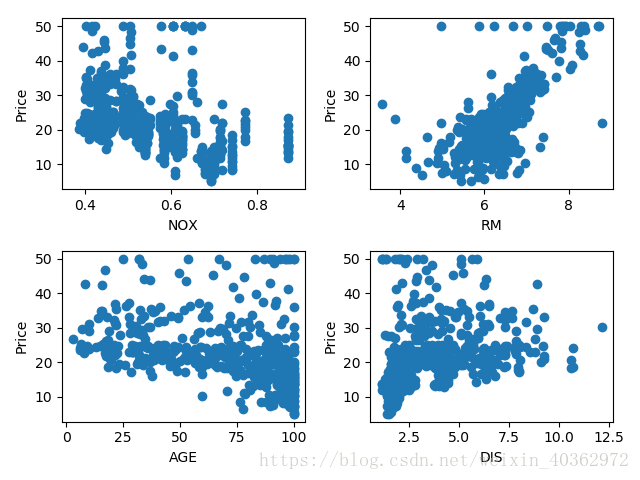
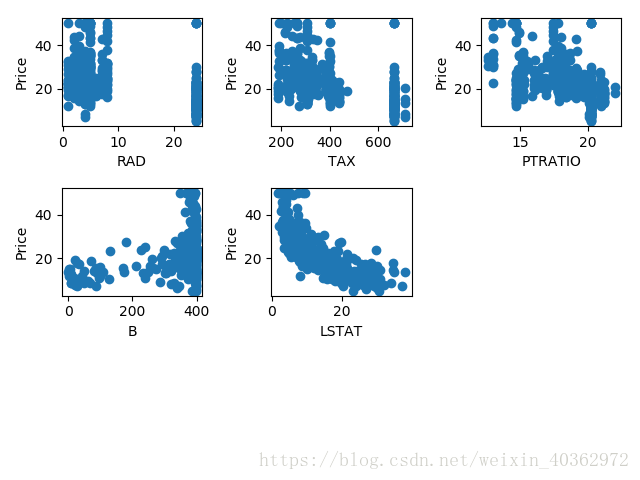
为了简化训练，只选择了第6个特征[‘RM’]来训练（第6个和最后一个特征的直观看上去比较符合线性回归），13个特征只在506个样本下比较难去拟合好。

下面是代码解释

#import data
boston=load_boston()
data=boston.data[:,(5)]
label=boston.target

#reshape column vector
data=data.reshape(-1,1)
label=label.reshape(-1,1)

因为这里我们只导入一列数据，我们需要把 [ ] reshape为[[ ]]，否则会报以下错误

Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.

接下来，对特征数据做特征缩放（对于单个特征来说，特征缩放的作用并不是特别大，但习惯起见，还是对其进行特征缩放，但是在多特征中，特征缩放显得尤其重要，可以加快梯度下降，见图）

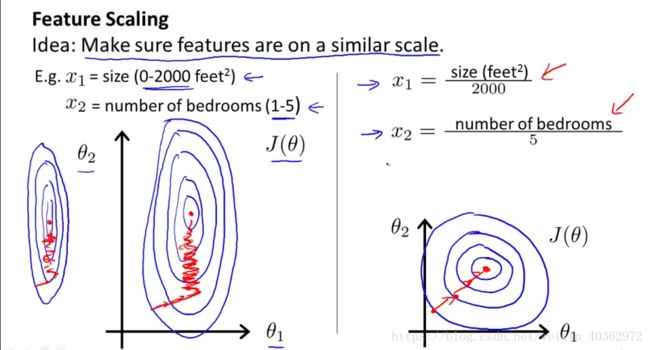
接下来就是定义一些占位符和权值、偏置等变量
偏置初始化0即可，权值最好不要初始化为0，使用正太分布随机值，如果使用0去初始化权值。在反向传播计算会出现不同权值变化量始终相同从而导致权值更新出现异常（推导见图）。

#getting number of training set & number of feature
m_feature=data.shape[1]
m_train=tf.placeholder(dtype=tf.float32)

x=tf.placeholder(dtype=tf.float32,shape=[None,m_feature],name='input')
y_=tf.placeholder(dtype=tf.float32,shape=[None,1],name='output')

#Define weights and offsets viriables
#Initialize weights using a Gaussian distribution
#Initialize the bias to 0
w=tf.Variable(tf.truncated_normal(shape=[m_feature,1],stddev=0.003,dtype=tf.float32))
b=tf.Variable(tf.zeros(shape=[1],dtype=tf.float32))

然后就是前向计算和反向计算，这个没有什么好说的，注意cost function的选择即可

#Forward calculation
y=tf.add(tf.matmul(x,w),b)


#use the mean square error function
learn_rate=0.08
loss=tf.reduce_sum(tf.pow(y_-y,2)/(2*m_train))
train_step=tf.train.GradientDescentOptimizer(learn_rate).minimize(loss)

这里我们定义一个list来存储训练过程中的loss值，再定义一个张量error来简单评估测试的误差

#variable train_loss is used to save the loss value of each iteration
train_loss =[]
#error
error = tf.reduce_mean(y-y_)

然后就开始进行训练
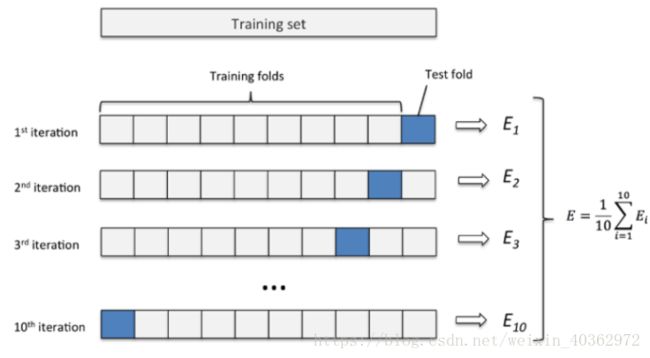
这里的重点在于数据集的划分，一开始用的是train_test_split将数据集划分成两份，70%为训练集，30%为测试集。但是听取别人建议后，使用k折交叉验证法。所谓k折交叉验证法，就是将数据集分成k份，每次取其中k-1份作为训练集，另外1份作为测试集，这样的好处是所有数据都有被利用，可以得到更好的参数，但是耗时会长一点（见图）。

with tf.Session() as sess:
    sess.run(init)
    for i in range(150):

        #k-fold cross validation
        kf=KFold(n_splits=10)
        for train_index,test_index in kf.split(data):
            X_train,X_test=data[train_index],data[test_index]
            Y_train,Y_test=label[train_index],label[test_index]
            w_,b_,_,l=sess.run(fetches=[w,b,train_step,loss], feed_dict={x: X_train, y_: Y_train,m_train:X_train.shape[0]})
            if i%10==0:
                print("Epoch {0} : error:{1}".format(i,sess.run(error,feed_dict={x:X_test,y_:Y_test})))
        train_loss.append(l)
        #print("Epoch {0} : loss{1}".format(i, l))

我用两种方法进行比较，首先是k（取10）折交叉验证的结果


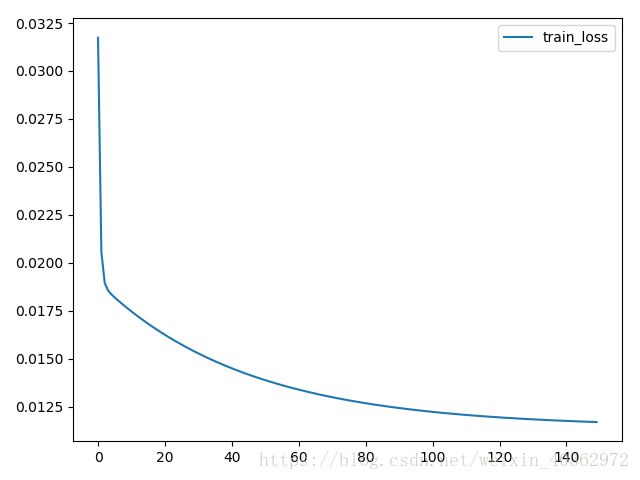
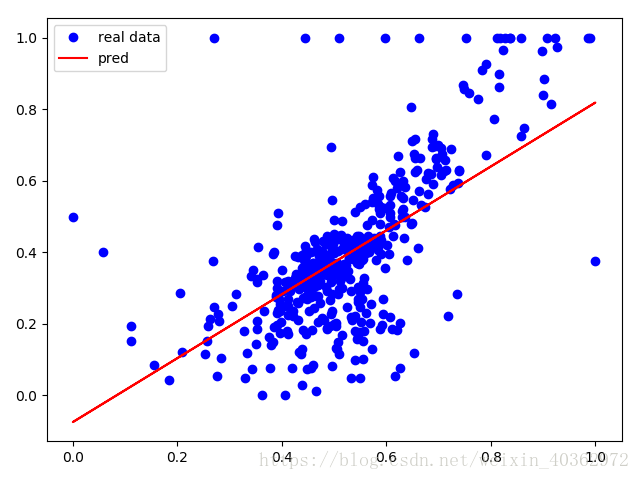
然后是train_test_split分类方法的结果


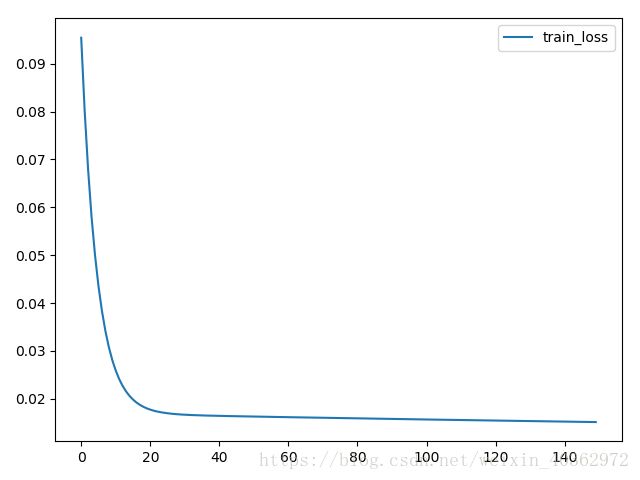
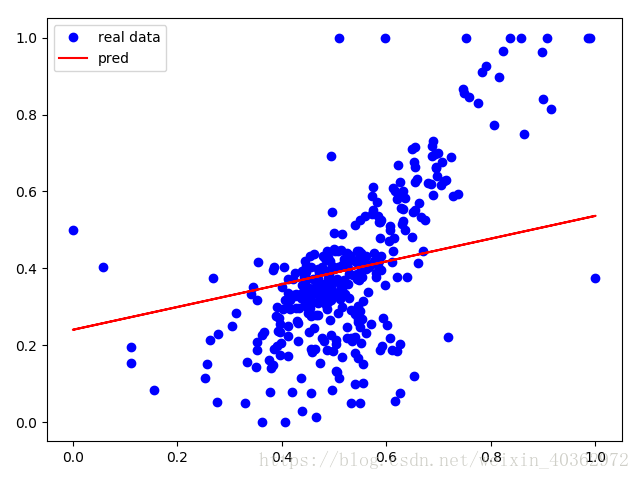
还是可以比较明显的看到，不管是loss值还是拟合程度。明显都是k折交叉验证法效果比较好。
完整代码请参考：https://github.com/LJP-Perfect/Machine-Learning/tree/master/Linear%20Regression

总结几点：
1、对特征进行选取
2、多特征时进行特征缩放
3、选取合适的cost function
4、使用k折交叉验证

还未解决的问题：
1、初始数据的分析
2、学习速率和k值的选取
3、选择更好的cost function