【简单dp】2080->最长公共子序列问题 动态规划

最长公共子序列问题

关于思路

因为比较菜所以只能写出dp的一些皮毛

我们用Ax表示序列A的连续前x项构成的子序列，即Ax= a1,a2,……ax, By= b1,b2,……by, 我们用LCS(x, y)表示它们的最长公共子序列长度，那原问题等价于求LCS(m,n)。为了方便我们用L(x, y)表示Ax和By的一个最长公共子序列。让我们来看看如何求LCS(x, y)。我们令x表示子序列考虑最后一项

1. Ax ＝ By
   那么它们L(Ax, By)的最后一项一定是这个元素！
   如果我们从序列Ax中删掉最后一项ax得到Ax-1,从序列By中也删掉最后一项by得到By-1，(多说一句角标为0时，认为子序列是空序列)，则我们从L(x,y)也删掉最后一项t得到的序列是L(x – 1, y - 1)。因此L(x, y) = L(x - 1, y - 1) 最后接上元素t。可以得到LCS(Ax, By) = LCS(x - 1, y - 1) + 1
2. Ax ≠ By
   仍然设t = L(Ax, By), 或者L(Ax, By)是空序列（这时t是未定义值不等于任何值）。则t ≠ Ax和t ≠ By至少有一个成立，因为t不能同时等于两个不同的值嘛！
   （2.1）如果t ≠ Ax，则有L(x, y)= L(x - 1, y)，因为根本没Ax的事嘛。
   LCS(x,y) = LCS(x – 1, y)
   （2.2）如果t ≠ By,l类似L(x, y)= L(x , y - 1)
   LCS(x,y) = LCS(x, y – 1)

可是，我们事先并不知道t，由定义，我们取最大的一个，因此这种情况下,有LCS(x,y) = max(LCS(x – 1, y) , LCS(x, y – 1))。
看看目前我们已经得到了什么结论：
LCS(x,y) =
(1) LCS(x - 1,y - 1) + 1 如果Ax ＝ By
(2) max(LCS(x – 1, y) , LCS(x, y – 1)) 如果Ax ≠ By
这时一个显然的递推式，光有递推可不行，初值是什么呢？
显然，==一个空序列和任何序列的最长公共子序列都是空序列！==所以我们有:

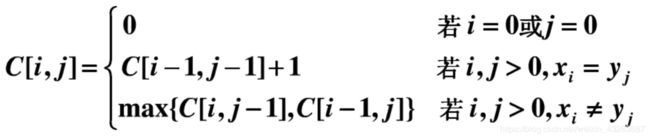也可以用图示演示一波：
综上所以我们可以得到最关键的最核心的伪代码：

for x = 0 to n do
    for y = 0 to m do
        if (x == 0 || y == 0) then 
            LCS(x, y) = 0
        else if (Ax == By) then
            LCS(x, y) =  LCS(x - 1,y - 1) + 1
        else 
            LCS(x, y) = ) max(LCS(x – 1, y) , LCS(x, y – 1))

注意： 我们这里使用了循环计算表格里的元素值，而不是递归，如果使用递归需要已经记录计算过的元素，防止子问题被重复计算。

关于代码

有了上面的分析就可以轻松解决最长公共子序列的问题了附上sdut oj上2080题最长公共子序列的代码：2080->最长公共子序列问题

#include
#include
#include
#define max(a, b) (((a) > (b)) ? (a):(b))//max函数定义方法一
int dp[505][505];
/*int max(int a, int b)//max函数定义方法二
{
    if(a <= b)
        return b;
    else
        return a;
}*/
int main()
{
    int i, j, t, n, m;
    char a[505], s[505];
    while(~scanf("%s %s", a+1, s+1))//让字符串从1开始主要为了防止下标越界。
    {
        n = strlen(a+1);
        m = strlen(s+1);
        memset(dp, 0, sizeof(dp));
        for(i = 1; i <= n; i++)
        {
            for(j = 1; j <= m; j++)
            {
                if(a[i]==s[j])//如果字符对应相等直接让dp[i][j]前一个加一。
                    dp[i][j] = dp[i-1][j-1] + 1;
                else//如果不等就让它等于前一个里最大的那个。
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        printf("%d\n", dp[n][m]);
    }
    return 0;
}

现在问题来了，我们如何得到一个最长公共子序列而仅仅不是简单的长度呢？其实我们离真正的答案只有一步之遥！注意(2.1)和(2.2) ，当LCS(x – 1, y) ＝ LCS(x, y – 1)时，其实走哪个分支都一样，虽然长度时一样的，但是可能对应不同的子序列，所以最长公共子序列并不唯一。又一个类似的递推公式。可见我们在计算长度LCS(x,y)的时候只要多记录一些信息，就可以利用这些信息恢复出一个最长公共子序列来。就好比我们在迷宫里走路，走到每个位置的时候记录下我们时从哪个方向来的，就可以从终点回到起点一样。
方法就是回溯法，直接附上核心代码。
回溯法一：

#include
#include
#define  MAXN  1002
char A[MAXN] = {0};
char B[MAXN] = {0};
char R[MAXN] = {0};
short dp[MAXN][MAXN] = {0};

//返回三个数的最大值
int max(int a, int b, int c)
{
    if(a > b)
    {
        b = a;
    }
    return  b > c ? b : c;
}

int main()
{
    int  i, j = 0, k;
    scanf("%s %s", A + 1, B + 1);
    for(i = 1; i <= strlen(A+1); i++)
    {
        for(j = 1; j <= strlen(B+1); j++)
        {
            dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1] + (A[i]==B[j] ? 1 : 0));
        }
    }
    i--;
    j--;
    k = MAXN - 1;
    while(i > 0 && j > 0)
    {
        if(A[i] == B[j])
        {
            R[k--] = A[i];
            i--;
            j--;
        }
        else if(dp[i-1][j] > dp[i][j-1])
        {
            i--;
        }
        else
        {
            j--;
        }
    }
    printf( "%s\n", R + k + 1);
    return 0;
}

回溯法二：（我们开一个数组，struct node { int x， y；}； node pre[N][N];这里的pre[i][j]:表示谁到达的i, j，这样就直接敲个递归就出来了。）

#include
#include
#include
#define max(a, b) (((a) > (b)) ? (a):(b))
#define N 3000
int dp[N][N];
char a[N], s[N];
struct node
{
    int x, y;
};
struct node pre[N][N];

void putLCS(int n, int m)
{
    if(pre[n][m].x == -1 && pre[n][m].y == -1)
        return;
    putLCS(pre[n][m].x, pre[n][m].y);
    if(pre[n][m].x == n-1 &&  pre[n][m].y == m-1)
        printf("%c", a[n]);
}

int main()
{
    int i, j, n, m;
    while(~scanf("%s %s", a+1, s+1))
    {
        memset(dp, 0, sizeof(dp));
        n = strlen(a+1);
        m = strlen(s+1);
        for(i = 0; i <= n; i++)
        {
            for(j = 0; j <= m; j++)
            {
                pre[i][j].x = -1;
                pre[i][j].y = -1;
            }
        }
        for(i = 1; i <= n; i++)
        {
            for(j = 1; j <= m; j++)
            {
                if(a[i]==s[j])
                {
                    dp[i][j] = dp[i-1][j-1] + 1;
                    pre[i][j].x = i-1;
                    pre[i][j].y = j-1;
                }
                else
                {
                    if(dp[i-1][j] > dp[i][j-1])
                    {
                        dp[i][j] = dp[i-1][j];
                        pre[i][j].x = i-1;
                        pre[i][j].y = j;
                    }
                    else
                    {
                        dp[i][j] = dp[i][j-1];
                        pre[i][j].x = i;
                        pre[i][j].y = j-1;
                    }
                }

            }
        }
        //printf("%d\n", dp[n][m]);
        putLCS(n, m);
        printf("\n");
    }
    return 0;
}

当然我们也可以用标记变量法，用一个二维数组用于标识下标走向，而这里的flag[x][y]的值是指下标怎么到这个位置的（可以参照上面的图示里的箭头分析）。在采用倒推法构造出公共子序列。但一定记得规定一个取值方向（比如说：相等取上）因为最长的子序列有多个如果不定很容易敲的时候思路乱了，也可能因为我是个菜鸡。。。

#include
#include
char a[500],b[500];
int num[501][501]; ///记录中间结果的数组
int flag[501][501];    ///标记数组，用于标识下标的走向，构造出公共子序列
void getLCS();    ///采用倒推方式求最长公共子序列

int main()
{
    scanf("%s %s", a, b);
    memset(num,0,sizeof(num));
    memset(flag,0,sizeof(flag));
    int i,j;
    for(i=1; i<=strlen(a); i++)
    {
        for(j=1; j<=strlen(b); j++)
        {
            if(a[i-1]==b[j-1])   ///注意这里的下标是i-1与j-1
            {
                num[i][j]=num[i-1][j-1]+1;
                flag[i][j]=1;  ///斜向下标记
            }
            else if(num[i][j-1]>num[i-1][j])
            {
                num[i][j]=num[i][j-1];
                flag[i][j]=2;  ///向右标记
            }
            else
            {
                num[i][j]=num[i-1][j];
                flag[i][j]=3;  ///向下标记
            }
        }
    }
    printf("%d\n",num[strlen(a)][strlen(b)]);
    getLCS();
    return 0;
}

void getLCS()
{
    char res[500];
    int i=strlen(a);
    int j=strlen(b);
    int k=0;    ///用于保存结果的数组标志位
    while(i>0 && j>0)
    {
        if(flag[i][j]==1)   ///如果是斜向下标记
        {
            res[k]=a[i-1];
            k++;
            i--;
            j--;
        }
        else if(flag[i][j]==2)  ///如果是斜向右标记
            j--;
        else if(flag[i][j]==3)  ///如果是斜向下标记
            i--;
    }

    for(i=k-1; i>=0; i--)
        printf("%c",res[i]);
}

最后说说现在对dp的浮浅认识：dp就是把原本很复杂不知道的解转化成已知的子问题，但问题在于如何转化，很自闭。以这题为例看到题该想到把到每个字母的最大子序列的值存起来，但不知道另一字符串对应的为多少就想到用二维数组保存起来，感觉有些类似于阶乘的感觉，求100的阶乘就求100*(99!),(99!)又是99*(98!)类推。
最后的最后安利点头网里面的教程很好很受用，文章中大部分都来自于他的教程。还有带我们学习的LJF学长，有他带着我们变强很好！

参考：
最长公共子序列问题（动态规划求解）；