最大流算法

最大流算法

网络流基础概念

网络流

在一个有向图$G=(V,E)$中：

• 有一个唯一的源点S(入度为$0$：出发点)
• 有一个唯一的汇点T(出度为$0$：结束点)
• 图中的每一条边都一个非负的权值，这个权值叫做容量$c(u,v)$

满足上述条件的图$G$称为网络流图，记为$G=(V,E,C)$

可以想象成，如果把每条边都看成一个管道，可以看成是水从源点S出发经过这些管道，最终流向汇点T，而每条管道有最大的容量。

例如：

可行流

流量：每条弧上给定一个实数$f(u,v)$，满足$0\le f(u,v)\le c(u,v)$

可行流满足：

• 源点S：流出量 = 整个网络的流量
• 汇点T：流入量 = 整个网络的流量
• 中间的点：总流入量 = 总流出量，同时$0\le f(u,v)\le c(u,v)$

这样的在整个网络中的流量就是可行流，可行流有多个

例如：

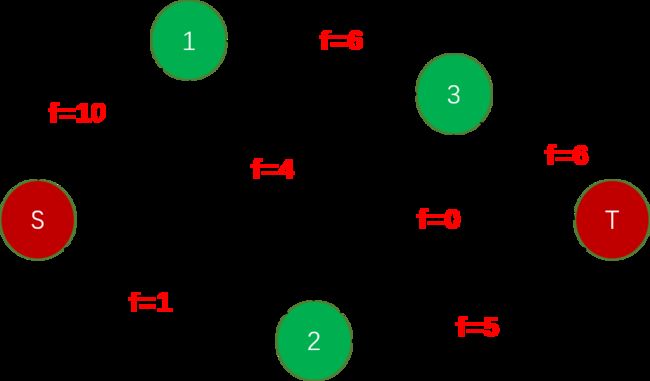
红色的部分表示流量，黑色的表示容量。可行流就是7

最大流

• 所有可行流中流量最大的流量
• 最大流可能不止一个

最大流为11

求解最大流算法

反向边

• 首先要明白一点，在一条从$S$到$T$的路径中，能够带来的最大流量取决于这条路径上的最小容量。

对于下面这张图$1$是源点,$4$是汇点

如果我们使用搜索算法找一条从1到4的路径，并且这条路径能够带来的流量是这条路径上边的容量的最小值，

假设我们找到的路径是$1->2->3->4$，现在的流量是$1$，因为这条路已经使用过了，把这条路径上的每条边减$1$，再次找从1到4的路径，发现找不到了，因此得到的答案为1，但是正确的答案应该是$2$。即$1->2->4$、$1->3->4$

这个时候，为了能够继续找到路径，必须要反向建立边，把当前路径反向建边，边的权值就是这条路径的流量

如图

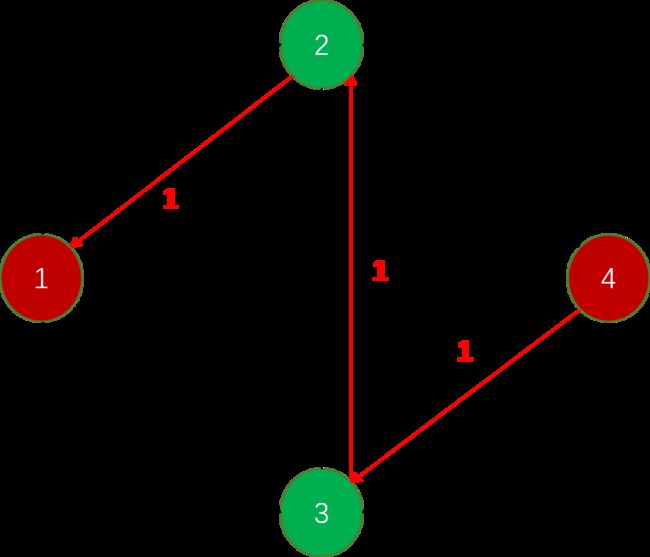
其中红色的边就是反向建立的，这个时候继续寻找一条路径，发现可以走$1->3->2->4$，带来的流量是$1$，然后继续找寻路径，发现没有可达的路径了，因此最大流是$1+1=2$。

为什么要反向建边呢，仔细想想应该能够明白，反向建立边的作用相当于让之前的路径有可以反悔的余地。这样即使一开始走错也没有关系，因为可以通过反向边来反悔，最终一定能得到正确答案

增广路经

明白了反向建边后，来看什么是增广路经？

如果一个可行流不是最大流，那么当前网络中一定存在一条增广路经。

从源点$S$到汇点$T$的一条路径中，如果边$(u,v)$与该路径的方向一致就称为正向边，否则就记为逆向边，如果在这条路径上的所有边满足

• 正向边$f(u,v)<c(u,v)$
• 逆向边$f(u,v)>0$

则该路径是增广路径

其实增广路径就是通过这样一条路径，来增加到达汇点的流量，而路径中的流量没到达容量。

(在上图中，其实每次找到的一条从$1$到$4$的路径都是一条增广路径)

沿这条增广路改进可行流的操作称为增广.所有可能的增广路径放在一起就构成了残余网络

以下这$2$个算法，都是基于不断找增广路经来实现的

EK算法

复杂度：$O(n{m}^2)$，$n$是点数，$m$是边数

首先要考虑的是怎么找增广路径，之前说用搜索算法，可以用$bfs$也可以用$dfs$，但是$bfs$的好处在于能够在残余网络中每一次找到最短的一条增广路径。因此在$EK$算法是基于$bfs$来找增广路经，$bfs$每执行一次，就找出一条增广路径来，然后把这条路径上的权值进行修改，同时反向建边。直到找不到增广路径为止，算法就结束了(代码注释写的很详细)

步骤

• 利用$bfs$找到一条最短增广路径，记录该路径的最小流量
• 利用一个数组把这个路径上的流量更新
• 不断重复$1,2$直到没有增广路径为止

具体实现：

POJ 1273（模板题）题目链接

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define N 205
#define INF 0x7fffffff
#define ll long long
ll min(ll a, ll b) {
	return a > b ? b : a;
}
using namespace std;
// Ek 找最大流，其中源点是1，汇点是n
ll g[N][N], pre[N], dis[N]; //g用来存图，pre[i]表示当前节点i的前一个节点，dis[i]表示从源点到i点的路径上的最小流量
ll n, m, s, t, ans;
queue <ll> q; 

ll bfs () { //找到一条增广路经， 返回这条路径的流量
	for(int i = 1; i <= n; i++) pre[i] = -1;
	while(!q.empty()) q.pop();
	q.push(s);
	dis[s] = INF;
	while (!q.empty()) {
		ll x = q.front();
		q.pop();
		if(x == t) break; //找到了汇点
		for(int i = 1; i <= n; i++) {
			if(pre[i] == -1 && g[x][i]) { //找到一个没有被访问且还有容量的点
				pre[i] = x;
				dis[i] = min(dis[x], g[x][i]); //更新增广路径上的最小流量
				q.push(i);
			}
		}
	}
	if(pre[t] == -1) return -1; //说明没有增广路径了，因此才走不到汇点
	else return dis[t];
}

void EK () { //更新残余网络的流量
	ll inc;
	while (1) {
		inc = bfs();
		if(inc == -1) break; //没有增广路径了，算法结束
		ll k = t;
		while (k != s) {
			g[k][pre[k]] += inc; //建立反向弧
			g[pre[k]][k] -= inc; //正向容量减去流量
			k = pre[k];
		}
		ans += inc;
	}
}

int main () {
	ll u, v, cost;
	while(scanf("%lld %lld", &m, &n) != EOF) { //读入数据，记得初始化
		memset(dis, 0, sizeof(dis));
		memset(g, 0, sizeof(g));
		ans = 0;
		s = 1, t = n;
		for(int i = 1; i <= m; i++) {
			scanf("%lld %lld %lld", &u, &v, &cost);
			g[u][v] += cost;
		}
		EK();
		printf("%lld\n", ans);
	}
	return 0;
}

Dinic算法

复杂度：$O(V^{2}E)$

$EK$算法找增广路径是基于$bfs$来进行的，$bfs$会把周围能够扩展的点全部扩展进来，直到找到汇点为止，相当于每找一次增广路径都要搜索大量的点。$Dinic$算法实际上是对$EK$的优化

$Dinic$算法利用$bfs$建立分层网络 (所谓分层网络，就是按照每一个点到源点的距离，分层，方便后面的$dfs$)。然后基于这个分层网络，使用$dfs$找到当前分层网络下的所有增广路径，并且做好相应的修改。然后不断重复这两个过程，直到无法分层为止，这样做只需要一次$bfs$就可以找到多条增广路径。

(PS:分层网络，就是利用$bfs$特性，源点为起点，一直扩散出去，每一个点都打一个标记，标记到源点的路径所经过的最少的弧的数量，假设用$dis[i]$表示$i$到源点S的最少经过的弧的数量，这样就可以将整个网络分层，基于这个分层网络，$dfs$找增广路径的时候，就可以找到最短的增广路径。如果当前点是$x$，$dfs$搜到下一个点$i$，一定要满足$dis[i]=dis[x]+1$，这样才是最短增广路径，效率才是最高的。)

步骤

• 利用$bfs$建立分层网络（记录每个节点的深度）
• 按照当前分层网络进行$dfs$(一层一层找)，找到所有该分层网络下的增广路径，并更新残余网络
• 重复$1、2$直到无法建立分层网络为止

邻接矩阵实现

POJ 1273（模板题）题目链接

#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
#define N 205
#define INF 0x7fffffff
#define min(a,b) a>b?b:a
using namespace std;

int n, m, s, t, maxflow;
int deep[N], g[N][N]; // deep 表示从源点到当前节点的深度
queue <int> q;

bool bfs () { //建立分层网络
	while(!q.empty()) q.pop();
	memset(deep, -1, sizeof(deep));
	deep[s] = 0; // 源点的深度为0
	q.push(s);
	while(!q.empty()) {
		int x = q.front();
		q.pop();
		for(int i = 1; i <= n; i++) {
			if(g[x][i] > 0 && deep[i] == -1) {// 如果有容量能够到达i，并且i节点的深度未被标记
				deep[i] = deep[x] + 1;
				q.push(i);
			}
		}
	}
	if(deep[n] > 0) return true; //能够建立分层图
	else return false; //不存在分层网络时，算法结束
}

//基于当前分层图，找到所有增广路径
int dfs (int x, int mx) { //表示当前节点x，以及这条增广路经上的最小流量
	int a;
	if(x == t) return mx;
	for(int i = 1; i <= n; i++) {
		if( g[x][i] > 0 && deep[i] == deep[x] + 1 && (a = dfs(i, min(mx, g[x][i]))) ) {//找到x能流通过去的的相邻顶点i
			g[x][i] -= a; //更新残余网络
			g[i][x] += a;
			return a;
		}
	}
	return 0;
}

void dinic () {
	while(bfs())
		maxflow += dfs(s, INF);
}

int main () {
	int u, v, cost;
	while(scanf("%d %d", &m, &n) != EOF) {
		s = 1, t = n;
		memset(g, 0, sizeof(g));
		maxflow = 0;
		for(int i = 1; i <= m; i++) {
			scanf("%d %d %d", &u, &v, &cost);
			g[u][v] += cost;
		}
		dinic();
		printf("%d\n", maxflow);
	}
	return 0;
}

链式前向星实现（内存小）

其中需要注意的细节：

• 存边的时候反边的容量设置为0；

• 假设$dfs$在递归回来的时候找到了这条增广路径的流量为$flow$，需要更新正反边

  • 正边：$edge[i].cap-=flow$
  • 反边：$edge[i\hat{}1].cap+=flow$
  • 其中$\hat{}$表示按位异或，如果$i$是偶数则$i\hat{}1=i+1$,如果$i$是奇数则$i\hat{}1=i-1$,为什么反边就是$i\hat{}1$呢。因此在存边的时候，是先存的正边，然后$++cnt$后存反边，正反边差$1$个，为了保证正边的编号是偶数，反边是奇数，$cnt$初始化为$-1$（因为我的习惯是写$++cnt$）

洛谷 网络最大流（题目链接）

#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
#define INF 0x7fffffff
#define N 10001
#define M 100005
using namespace std;

struct flow {
	int to, next, cap;
}edge[M * 4];

int n, m, s, t, maxflow;
int cnt = -1;
int head[N], dep[N]; //其中dep[i]表示i的深度，也就是到源点的最小边数	
queue <int> q;
inline void addEdge (int u, int v, int cost) {
	edge[++cnt].to = v;
	edge[cnt].cap = cost;
	edge[cnt].next = head[u];
	head[u] = cnt;
	//反向建边，容量为0
	edge[++cnt].to = u;
	edge[cnt].cap = 0;
	edge[cnt].next = head[v];
	head[v] = cnt;
}

bool bfs () { //建立分层网络
	while(!q.empty()) q.pop();
	memset(dep, -1, sizeof(dep));
	dep[s] = 0;
	q.push(s);
	while(!q.empty()) {
		int x = q.front(); q.pop();
		for(int i = head[x]; i != -1; i = edge[i].next) {
			int u = edge[i].to;
			int cap = edge[i].cap;
			if(cap > 0 && dep[u] == -1) {
				dep[u] = dep[x] + 1;
				q.push(u);
			}
		}
	}
	if(dep[t] == -1) return 0;
	else return 1;
}

int dfs (int x, int mx) { 
	int a;
	if(x == t) return mx; //找到汇点，返回
	for(int i = head[x]; i != -1; i = edge[i].next) {
		int u = edge[i].to;
		int cap = edge[i].cap;
		if(cap > 0 && dep[u] == dep[x] + 1 && (a = dfs(u, min(cap, mx))) ) {
			edge[i].cap -= a; 
			edge[i^1].cap += a; //反向边
			return a;
		}
	}
	return 0; //搜不到增广路经了就返回0
} 

void dinic () {
	int res;
	while ( bfs() )  //当前网络下，搜索所有的增广路径
		while (1) {
			res = dfs(s, INF); //加上该路径能带来的流量
			if(!res) break;
			maxflow += res;
		}
}

int main () {
	int u, v, cost;
	memset(head, -1, sizeof(head));
	scanf("%d %d %d %d", &n, &m, &s, &t);
	for(int i = 1; i <= m; i++) {
		scanf("%d %d %d", &u, &v, &cost);
		addEdge(u, v, cost);
	}
	dinic();
	printf("%d", maxflow);
	return 0;
}

算法还可以优化，加入一个$cur$数组。

首先要明白在$dfs$找增广路径的时候，一定是完全增广的，也就是说这条路径使用过后，下一次不必再次检查这条路径了。直接从下一条边开使找，加入这个优化，算法能快不少

int cur[N];
bool bfs () {
	while(!q.empty()) q.pop();
	for(int i = 0; i <= n; i++) cur[i] = head[i]; //复制head数组
	memset(dep, -1, sizeof(dep));
	dep[s] = 0;
	q.push(s);
	while(!q.empty()) {
		int x = q.front(); q.pop();
		for(int i = head[x]; i != -1; i = edge[i].next) {
			int u = edge[i].to;
			int cap = edge[i].cap;
			if(cap > 0 && dep[u] == -1) {
				dep[u] = dep[x] + 1;
				q.push(u);
			}
		}
	}
	if(dep[t] == -1) return 0;
	else return 1;
}
int dfs (int x, int mx) {
	int a;
	if(x == t) return mx;
	for(int i = cur[x]; i != -1; i = edge[i].next) {
		cur[x] = i; //避免了搜寻已经增广过的路径
		int u = edge[i].to;
		int cap = edge[i].cap;
		if(cap > 0 && dep[u] == dep[x] + 1 && (a = dfs(u, min(cap, mx))) ) {
			edge[i].cap -= a;
			edge[i^1].cap += a; //反向边
			return a;
		}
	}
	return 0; //搜不到增广路经了就返回0
}