LeetCode 第187场周赛 题解
文章目录
- a.旅行终点站
- a.题目
- a.分析
- a.参考代码
- b.是否所有 1 都至少相隔 k 个元素
- b.题目
- b.分析
- b.参考代码
- c.绝对差不超过限制的最长连续子数组
- c.题目
- c.分析
- c.参考代码
- d.有序矩阵中的第 k 个最小数组和
- d.题目
- d.分析
- d.暴力
- d.基于最小堆的bfs
- d.参考代码
- d.暴力代码
- d.优先队列bfs代码
a.旅行终点站
a.题目
给你一份旅游线路图,该线路图中的旅行线路用数组 paths 表示,其中 paths[i] = [cityAi, cityBi] 表示该线路将会从 cityAi 直接前往 cityBi 。请你找出这次旅行的终点站,即没有任何可以通往其他城市的线路的城市。
题目数据保证线路图会形成一条不存在循环的线路,因此只会有一个旅行终点站。
示例 1
输入:paths = [[“London”,“New York”],[“New York”,“Lima”],[“Lima”,“Sao Paulo”]]
输出:“Sao Paulo”
解释:从 “London” 出发,最后抵达终点站 “Sao Paulo” 。本次旅行的路线是 “London” -> “New York” -> “Lima” -> “Sao Paulo” 。
示例 2
输入:paths = [[“B”,“C”],[“D”,“B”],[“C”,“A”]]
输出:“A”
解释:所有可能的线路是:
“D” -> “B” -> “C” -> “A”.
“B” -> “C” -> “A”.
“C” -> “A”.
“A”.
显然,旅行终点站是 “A” 。
示例 3
输入:paths = [[“A”,“Z”]]
输出:“Z”
提示
- 1 <= paths.length <= 100
- paths[i].length == 2
- 1 <= cityAi.length, cityBi.length <= 10
- cityAi != cityBi
- 所有字符串均由大小写英文字母和空格字符组成。
a.分析
注意看题目我们的要求是:
没有任何可以通往其他城市的线路的城市
然后我们知道已知条件(a,b)表示以a为起点b为终点
那么题目就可以转化为找到一个城市从来没有出现在a这个位置上的即可 (题目保证只有一个城市满足)
于是我们就可以暴力的找到这个满足上一行的条件的城市了
- 首先先把所有在a位置出现过的城市放进一个set或hash set里面
- 再把全部的a和b位置都遍历下 看下哪个没有城市没有出现在set里面 它就是答案
假设n是path的数量 放在set里面的复杂度就是O(nlogn)或者O(n)
遍历的时候看有没有在set的复杂度是O(nlogn)或者O(n)
于是总的时间复杂度为O(nlogn)或O(n) (取决于用哪个set存放)
a.参考代码
class Solution {
public:
string destCity(vector<vector<string>>& paths) {
unordered_set<string> s;
for(auto &i:paths) //把全部在a位置上的都放进数组
s.insert(i[0]);
for(auto &i:paths)
{
if(!s.count(i[0]))return i[0]; //没出现的过的
if(!s.count(i[1]))return i[1]; //没出现过的
}
return ""; //实际不会有这个返回值
}
};
b.是否所有 1 都至少相隔 k 个元素
b.题目
给你一个由若干 0 和 1 组成的数组 nums 以及整数 k。如果所有 1 都至少相隔 k 个元素,则返回 True ;否则,返回 False 。
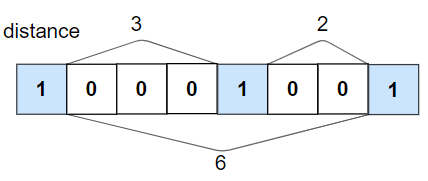
输入:nums = [1,0,0,0,1,0,0,1], k = 2
输出:true
解释:每个 1 都至少相隔 2 个元素。
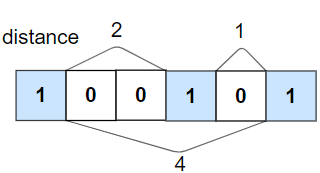
输入:nums = [1,0,0,1,0,1], k = 2
输出:false
解释:第二个 1 和第三个 1 之间只隔了 1 个元素。
示例 3
输入:nums = [1,1,1,1,1], k = 0
输出:true
示例 4
输入:nums = [0,1,0,1], k = 1
输出:true
提示
- 1 <= nums.length <= 10^5
- 0 <= k <= nums.length
- nums[i] 的值为 0 或 1
b.分析
按照题目模拟一遍就好了
即检查两个1之间有多少个0是否不小于k
- 开一个计数器
- 当碰到1的时候就检测计数器的计数 然后把它置零
- 碰到0的时候计数器**+1**
- 初始化的时候把计数器置为k (因为第一个1和左边没有相隔 必定符合条件)
总的时间复杂度就只有遍历数组的O(n)
b.参考代码
class Solution {
public:
bool kLengthApart(vector<int>& nums, int k) {
int flag=k; //计数器
for(int i=0;i<nums.size();i++)
{
if(nums[i]) //碰到1
if(flag<k)return false; //不符合条件
else flag=0; //置为零
else flag++; //计数器自增
}
return true;
}
};
c.绝对差不超过限制的最长连续子数组
c.题目
给你一个整数数组 nums ,和一个表示限制的整数 limit,请你返回最长连续子数组的长度,该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。
如果不存在满足条件的子数组,则返回 0 。
示例 1
输入:nums = [8,2,4,7], limit = 4
输出:2
解释:所有子数组如下:
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4.
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4.
因此,满足题意的最长子数组的长度为 2 。
示例 2
输入:nums = [10,1,2,4,7,2], limit = 5
输出:4
解释:满足题意的最长子数组是 [2,4,7,2],其最大绝对差 |2-7| = 5 <= 5 。
示例 3
输入:nums = [4,2,2,2,4,4,2,2], limit = 0
输出:3
提示
- 1 <= nums.length <= 10^5
- 1 <= nums[i] <= 10^9
- 0 <= limit <= 10^9
c.分析
看到这个题目连续字串的字眼 很容易联想到滑动窗口
再思考一下 对于每个以第i个数结尾的最长子串 最长长度为以第i-1结尾的最长子串+1
也就是说 加入新的数字 只会有加入这个数到子串 和可能需要的舍弃前面一部分这两种操作
不需要对前面的数进行加入操作 因此我们可以保存着一个窗口 然后到新的数的时候改变窗口大小
在窗口里面的数必定符合任何一个数和任何一个数的绝对值差都不大于limit
我们考虑新加进来的数会对窗口有什么影响 暴力的想法就是对窗口内的每个数从右到左进行计算绝对值差 如果大于了limit就直接截断 把左边的都踢出窗口
这样子暴力最坏的情况是左边的数都符合 那么是O(n^2)的时间复杂度 是不能接受的
优化思考
可以看出暴力的问题在于找到需要截断的位置太慢了
思考一下可以发现以下问题
- 如果新加进来的数非常的大 但在计算的途中碰到了窗口的最小值 并且计算完后发现符合 那么这个时候剩下的计算都是多余的了
- 如果新的数非常小 且同理计算完窗口最大值后也还符合 那么剩下的计算也是多余的了
- 新加的数恰好在窗口最大最小值之间 分别计算与窗口最大最小值的关系 如果发现最大最小值都符合 那么其他计算也是多余的
都是关于最大最小值的问题 那么这时候就可以想到使用最大堆和最小堆来维护窗口最大最小值
那么肯定不会所有情况都能像上面三种情况那么顺利 假如不符合怎么办呢
当出现不符合情况的最大/最小值的时候把该最大/最小值以及在他左边的次大/次小全部弹出堆 直到某个最大/最小值符合以上三种情况 那么他右边的数就都符合情况了
我们并不需要考虑堆里面的数是否符合 因为只需要同时保存下标 就能直接知道符合情况的最大最小值的右边有多少个数了
总的来说就是通过不断调整对顶来找到窗口的最左端
堆维护最大最小值的代价是O(logn) 只需要遍历一次原数组O(n)
所以总的时间复杂度为O(nlogn)
c.参考代码
class Solution {
public:
int longestSubarray(vector<int>& nums, int limit) {
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> small; //最小堆
priority_queue<pair<int,int>,vector<pair<int,int>>,less<pair<int,int>>> big; //最大堆
int ans=0;
int x=-1; //窗口最左端
for(int i=0;i<nums.size();i++)
{
small.push({nums[i],i}); //把当前数(数值,下标)先进大小堆 因为判断到当前数的话 自己和自己相减绝对差为0肯定符合
big.push({nums[i],i});
if(nums[i]>=big.top().first){ //当前数非常大
while(nums[i]-small.top().first>limit){ //调整最小值 直到找到符合的
x=small.top().second; //窗口最左端
small.pop();
while(small.top().second<x)small.pop(); //把窗口最左端还左的都剔除掉
while(big.top().second<x)big.pop();
}
}
else if(nums[i]<=small.top().first){ //当前数非常小
while(big.top().first-nums[i]>limit){
x=big.top().second;
big.pop();
while(small.top().second<x)small.pop(); //同上
while(big.top().second<x)big.pop();
}
}
else { //当前数在中间 把比当前数大和小的数看成两堆就好
while(nums[i]-small.top().first>limit){ //上面情况的copy
x=small.top().second;
small.pop();
while(small.top().second<x)small.pop();
while(big.top().second<x)big.pop();
}
while(big.top().first-nums[i]>limit){ //上面情况的copy
x=big.top().second;
big.pop();
while(small.top().second<x)small.pop();
while(big.top().second<x)big.pop();
}
}
ans=max(ans,i-x);
}
return ans;
}
};
d.有序矩阵中的第 k 个最小数组和
d.题目
给你一个 m * n 的矩阵 mat,以及一个整数 k ,矩阵中的每一行都以非递减的顺序排列。
你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个 最小 数组和。
示例 1
输入:mat = [[1,3,11],[2,4,6]], k = 5
输出:7
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,2], [1,4], [3,2], [3,4], [1,6]。其中第 5 个的和是 7 。
示例 2
输入:mat = [[1,3,11],[2,4,6]], k = 9
输出:17
示例 3
输入:mat = [[1,10,10],[1,4,5],[2,3,6]], k = 7
输出:9
解释:从每一行中选出一个元素,前 k 个和最小的数组分别是:
[1,1,2], [1,1,3], [1,4,2], [1,4,3], [1,1,6], [1,5,2], [1,5,3]。其中第 7 个的和是 9 。
示例 4
输入:mat = [[1,1,10],[2,2,9]], k = 7
输出:12
提示
- m == mat.length
- n == mat.length[i]
- 1 <= m, n <= 40
- 1 <= k <= min(200, n ^ m)
- 1 <= mat[i][j] <= 5000
- mat[i] 是一个非递减数组
d.分析
假设n为行数 m为列数
d.暴力
最最暴力的做法是对每一行的每一个都与其他排列组合看看
且维护前k个和 复杂度爆炸O(n^m) 维护和的复杂度太小可以省略
上述暴力肯定不行 很明显的问题在于 基本不会出现每行都选取最大的几个数 几个大的数往后移再选取更大的数就是再浪费时间
所以很容易就能想到优化了一点的暴力:
考虑我们已经暴力选取到第i行了 假如我们已经知道了前面i-1行的前k个和是多少
我们就可以通过对当前i行所有数字都去尝试加上前面的和形成新的和 这一步是一个O(mk)的两次循环遍历
再通过一边插入一边排序O(loga)把第i行前k个和弄出来 这里的a是 m个数和k个和形成的笛卡尔积为mk
那么我们就可以通过O(nmklogmk)的暴力得出前k个和是多少 大概是40×40×200×15=4,800,000 实际边插入边排序大一点勉强可以过
简单证明:
显然无论如何选取第i行的数x 数x和第k+1个和相加总会比x和1~k个和相加的要大 那么就总能生成k个比他小的数 所以往后的和就没有用了
我们要用到第i行全部数是因为有可能第i行第m个数加上上一行第一个和要比第i行第1个数加上上一行第二个和要小
d.基于最小堆的bfs
傻子都知道 最小的和当然就是每一行都选第一个 那么问题来了下一个大的是哪个呢?
想了下发现 下一个一定是出现在某一行选第二个其他都选第一个的集合里 废话
也就是说我们可以通过这个方法 一次某行前进一步来得到大小为n的一个集合 这个集合的数都是比当前的和大那么点点 一定存在当前和(即当前层)的下一个和
但是也仅仅会出现当前和的下一个和 不能保证和之前层的和相比还是小的
足够证明了这样子走出一步可以得到包含下一个和的集合而不会漏掉
我们发现这样子一步得出一些集合有点像bfs 而且还要每步都要最小的作为当前步 包括当前层和之前层的 那么自然就能想到用优先队列(最小堆)来储存
那么整个算法的步骤就是:
- 初始状态为全部选0号位置的
- 对当前状态每行都进行前进一步的状态保存到优先队列中
- 优先队列队首状态是最小的 让它出队
- 基于出队的状态再把下一步全部可能的状态保存到优先队列中
- 重复k次就能得到答案
每次O(n)把n个状态加入最小堆中 需要k次加入操作 每次加入堆都要O(lognk)来调整
所以总的时间复杂度为O(nklognk)
实际实现时候需要用一个数组把每行选第几个这样的状态存下来 这个状态的copy需要O(n)
而且状态不能遍历到重复的 因此我们需要一个set来去重状态
set的插入时O(lognk)的 vector的比较是O(n)的 所以这里会有O(nlognk)的开销
所以实际会去到O((n3)(lognk)2) 且相关操作的常数会很大
d.参考代码
d.暴力代码
class Solution {
public:
int kthSmallest(vector<vector<int>>& mat, int k) {
multiset<int> s(mat[0].begin(),mat[0].end()); //multiset自动边插入边排序 初始时多一点没关系
for(int i=1;i<mat.size();i++){ //遍历每一行
multiset<int> t; //当前行新出现的和
for(auto j:s) //每个和
for(auto k:mat[i]) //当前行每个数
t.insert(j+k);
auto it=t.begin();
s.clear();
for(int j=0;j<min((int)t.size(),k);j++,it++)
s.insert(*it); //把前k个和更新了
}
return *s.rbegin(); //第k个
}
};
d.优先队列bfs代码
class Solution {
public:
int kthSmallest(vector<vector<int>>& mat, int k) {
int n=mat.size(),m=mat[0].size();
vector<int> state(n,0); //保存每一行选选第几列的状态
priority_queue<pair<int,vector<int>>,vector<pair<int,vector<int>>>,greater<pair<int,vector<int>>>> q; //第一个是和 用来排序 第二个是用来转移状态的
set<vector<int>> exist; //状态去重
int sum=0;
for(int i=0;i<n;i++)sum+=mat[i][0]; //第一个状态的和
q.push({sum,state});
for(int i=1;i<k;i++){ //k次操作
auto now=q.top();
sum=now.first;
state=now.second;
q.pop();
for(int j=0;j<n;j++){ //每一行都尝试往后
if(state[j]+1==m)continue; //不能向后改状态
vector<int> t=state;
t[j]++;
if(exist.count(t))continue;
int s=sum;
s+=mat[j][t[j]]-mat[j][state[j]]; //更新下和
q.push({s,t});
exist.insert(t);
}
}
return q.top().first;
}
};