LeetCode 第191场周赛 题解

比完赛吃完饭太累直接睡到晚上 题解出迟了

a.数组中两元素的最大乘积

a.题目

给你一个整数数组 nums，请你选择数组的两个不同下标 i 和 j，使 (nums[i]-1)*(nums[j]-1) 取得最大值。
请你计算并返回该式的最大值。

示例 1

输入：nums = [3,4,5,2]
输出：12
解释：如果选择下标 i=1 和 j=2（下标从 0 开始），则可以获得最大值，(nums[1]-1)(nums[2]-1) = (4-1)(5-1) = 3*4 = 12 。

示例 2

输入：nums = [1,5,4,5]
输出：16
解释：选择下标 i=1 和 j=3（下标从 0 开始），则可以获得最大值 (5-1)*(5-1) = 16 。

示例 3

输入：nums = [3,7]
输出：12

提示

• 2 <= nums.length <= 500

• 1 <= nums[i] <= 10^3

a.分析

500的复杂度 直接两两相乘爆破就行了
判断一下i和j下标不能相同是要注意的 不过测试下样例就能知道
总的复杂度是O(n^2)

a.参考代码

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int Max=0;
        for(int i=0;i<nums.size();i++)	//爆破
            for(int j=0;j<nums.size();j++)
                if(i==j)continue;
                else Max=max(Max,(nums[i]-1)*(nums[j]-1));
        return Max;
    }
};

b.切割后面积最大的蛋糕

b.题目

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离，类似地， verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。
请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果对 10^9 + 7 取余后返回。

示例 1

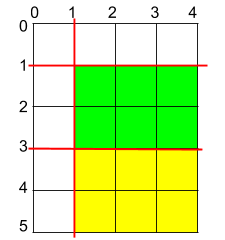
输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示

• 2 <= h, w <= 10^9

• 1 <= horizontalCuts.length < min(h, 10^5)
• 1 <= verticalCuts.length < min(w, 10^5)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• 题目数据保证 horizontalCuts 中的所有元素各不相同
• 题目数据保证 verticalCuts 中的所有元素各不相同

b.分析

显然 面积和宽和高有关 而宽和高思考下不难得出是独立的 也就是你任取一个高的区间和一个宽的区间对应 都会有一个面积
那么显然只要找到间隔最大的宽和高就行了

由于给定的数组是乱序的 所以排序下可以更好去进行两两相邻的计算间隔

注意边界并没有给出来 所以可以自己把边界插入下
注意可能会爆int

总的复杂度是O(n)

b.参考代码

class Solution {
public:
    const int mod=1e9+7;
    int maxArea(int h, int w, vector<int>& hc, vector<int>& vc) {
        hc.push_back(0);
        hc.push_back(h);
        vc.push_back(0);
        vc.push_back(w);
        sort(hc.begin(),hc.end());
        sort(vc.begin(),vc.end());
        int H=0,W=0;
        for(int i=1;i<hc.size();i++)
            H=max(H,hc[i]-hc[i-1]);
        for(int i=1;i<vc.size();i++)
            W=max(W,vc[i]-vc[i-1]);
        long long ans=1ll*H*W;
        return (ans%mod);
    }
};

c.数组中两元素的最大乘积

c.题目

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。
路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。
请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

示例 1

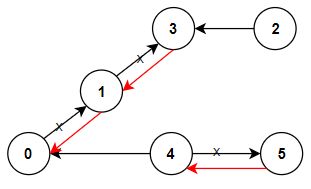
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 2

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 3

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

提示

• 2 <= n <= 5 * 10^4

• connections.length == n-1
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] <= n-1
• connections[i][0] != connections[i][1]

c.分析

其实这道题的最小是迷惑性 因为是树 所以两个点之间的路径是唯一的 那么答案其实就是唯一的 直接模拟做就行了

• 把全部能从0号点出发的边都反向
• 把全部不能达到0号点的边全部都要反向

直接按照上面两个点来跑两个dfs模拟就行了

至于为什么dfs写两个 因为我觉得在一个dfs特判从0号点出发的情况 很麻烦 因为从0号点出发直接就到达0了

必须先跑从0号点出发的反向边 因为如果不跑这个的话 其他可能永远都到不了0

总的复杂度是遍历整棵树的O(n)

c.参考代码

class Solution {
public:
    vector<set<int>> G;
    int ans;
    int minReorder(int n, vector<vector<int>>& c) {
        G.resize(n);
        for(auto i:c)
            G[i[0]].insert(i[1]);
        dfs1(0);	//先跑第一点
        for(int i=1;i<n;i++)
            dfs2(i);	//再跑第二点
        return ans;
    }
    void dfs1(int x)
    {
        vector<int> v;
        for(auto i:G[x])	//我这里没有思考 怕set删除后迭代器会失效 所以新开了个数组存
            v.push_back(i);
        for(auto i:v)
        {
            dfs1(i);
            G[i].insert(x);		//全部从0出发的边都要反向
            G[x].erase(i);
            ans++;
        }
    }
    bool dfs2(int x)
    {
        if(!x)return true;
        if(!G[x].size())return false;
        bool ret=false;
        vector<int> v;
        for(auto i:G[x])	//我这里没有思考 怕set删除后迭代器会失效 所以新开了个数组存
            v.push_back(i);
        for(auto i:v){
            bool flag=dfs2(i);
            if(!flag){	//不可达0
                G[i].insert(x);
                G[x].erase(i);
                ans++;
            }
            else ret=true;
        }
        return ret;
    }
};

d.两个盒子中球的颜色数相同的概率

d.题目

桌面上有 2n 个颜色不完全相同的球，球上的颜色共有 k 种。给你一个大小为 k 的整数数组 balls ，其中 balls[i] 是颜色为 i 的球的数量。
所有的球都已经 随机打乱顺序 ，前 n 个球放入第一个盒子，后 n 个球放入另一个盒子（请认真阅读示例 2 的解释部分）。
注意：这两个盒子是不同的。例如，两个球颜色分别为 a 和 b，盒子分别为 [] 和 ()，那么 [a] (b) 和 [b] (a) 这两种分配方式是不同的（请认真阅读示例 1 的解释部分）。
请计算「两个盒子中球的颜色数相同」的情况的概率。

示例 1

输入：balls = [1,1]
输出：1.00000
解释：球平均分配的方式只有两种：

• 颜色为 1 的球放入第一个盒子，颜色为 2 的球放入第二个盒子
• 颜色为 2 的球放入第一个盒子，颜色为 1 的球放入第二个盒子
  这两种分配，两个盒子中球的颜色数都相同。所以概率为 2/2 = 1 。

示例 2

输入：balls = [2,1,1]
输出：0.66667
解释：球的列表为 [1, 1, 2, 3]
随机打乱，得到 12 种等概率的不同打乱方案，每种方案概率为 1/12 ：
[1,1 / 2,3], [1,1 / 3,2], [1,2 / 1,3], [1,2 / 3,1], [1,3 / 1,2], [1,3 / 2,1], [2,1 / 1,3], [2,1 / 3,1], [2,3 / 1,1], [3,1 / 1,2], [3,1 / 2,1], [3,2 / 1,1]
然后，我们将前两个球放入第一个盒子，后两个球放入第二个盒子。
这 12 种可能的随机打乱方式中的 8 种满足「两个盒子中球的颜色数相同」。
概率 = 8/12 = 0.66667

示例 3

输入：balls = [1,2,1,2]
输出：0.60000
解释：球的列表为 [1, 2, 2, 3, 4, 4]。要想显示所有 180 种随机打乱方案是很难的，但只检查「两个盒子中球的颜色数相同」的 108 种情况是比较容易的。
概率 = 108 / 180 = 0.6 。

示例 4

输入：balls = [3,2,1]
输出：0.30000
解释：球的列表为 [1, 1, 1, 2, 2, 3]。要想显示所有 60 种随机打乱方案是很难的，但只检查「两个盒子中球的颜色数相同」的 18 种情况是比较容易的。
概率 = 18 / 60 = 0.3 。

示例 5

输入：balls = [6,6,6,6,6,6]
输出：0.90327

提示：

1 <= balls.length <= 8
1 <= balls[i] <= 6
sum(balls) 是偶数
答案与真实值误差在 10^-5 以内，则被视为正确答案

d.分析

数学概率问题
首先我们肯定要算出分母的对吧
分母的算法是一个古典概型的可重复排列数
公式为n!/(k0!k1!..km!) n为全部数的个数(含重复) m个不重复的数 km指的是第几个数有几个重复的
那么知道公式之后就能把分母全部情况给算出来

思考符合题意的有多少种:
我们可以把左边盒子和右边盒子选取的情况用数组体现
比如说原来的balls为 [3,2,1] 那么左边left可能选择了[1,2,0] 那么右边自然就是剩下的[2,0,1] 考虑这样子的选取是否符合题意
那么对于这个left和right是可以用dfs来遍历全部情况的 每一位最多选7种(0~6) 然后最多有8位 那么全部情况就是7的8的次方那么多种情况

那么对于left和right的选取之后 很显然盒子的内部是可以乱序的 那么盒子的内部也是应用可重复排列数计算公式来计算有多少种情况 那么对于确定的left和right 他们总的事件是概率乘法原理 直接相乘就完事了

这里有个点就是 48的阶乘非常大 但是这题要求的精度很低 所以直接double就行了 不然的话还得上高精度整数 或者直接python吧…

总的复杂度是枚举的7^8乘上计算可重复排列数需要的常数时间

d.参考代码

class Solution {
public:
    double getProbability(vector<int>& balls) {
        vector<int> left(balls.size(),0);
        vector<int> right(balls.size(),0);
        return dfs(0,balls,left,right,accumulate(balls.begin(),balls.end(),0),0,0)/get(balls);
    }
    double fact(int n)	//阶乘 用double暴力存
    {
        double ans=1;
        for(int i=1;i<=n;i++)ans*=i;
        return ans;
    }
    double get(vector<int> &balls)	//可重复全排列公式
    {
        int sum=accumulate(balls.begin(),balls.end(),0);
        double ans=fact(sum);
        for(auto i:balls)
            ans/=fact(i);
        return ans;
    }
	//x是枚举到第几位 balls原来的球 left right 左右的球种类选取
	// ts 总的球数 ls 左边的球数 rs右边的球数 是用来剪枝判断要左右球数相等的
    double dfs(int x,vector<int>& balls,vector<int> &left,vector<int> &right,int ts,int ls,int rs)
    {
        if(ls*2>ts || rs*2>ts)return 0.0;	//剪枝 因为后面一直都在增加 所以不可能相等
        if(x==balls.size()){	//选完了数 (枚举完最后一位了)
            int l=0,r=0;	//计算分别有多少个不同颜色的
            for(auto i:left)if(i)l++;
            for(auto i:right)if(i)r++;
            if(l!=r)return 0.0;		//个数不等
            return get(left)*get(right);	//事件乘法原理
        }
        double ans=0;
        for(int i=0;i<=balls[x];i++){
            left[x]=i;
            right[x]=balls[x]-i;
            ans+=dfs(x+1,balls,left,right,ts,ls+left[x],rs+right[x]);
        }
        return ans;
    }
};