2019广东工业智造创新大赛【赛场二】感谢拼命的自己

1赛前感想

这个比赛呢，是去年参加的，开始接触比赛的时候完全不会，也不知道干什么，一头雾水，看到密密麻麻的数据总觉的头皮发麻。比较宽慰的是，慢慢的有了一点点基本的思路，然后就投入进去，最后的结果不论。只是感觉当时一头热血，因为那时候正好是大二学期开学不久，我们也开始正式的学习专业课程，学习任务挺重的。一边准备着下一门学科的预习任务，一边准备着这门学科的小论文，加上备考英语的自己，真的很想放弃。感谢少年的自己能够有如此锐气去披荆斩棘，咬牙坚持。我选择了继续下去。给我们推荐这个比赛的导师，问我们几个人，你们可以试着参加一下，而当时，我们几个人想法出乎意外的一致**“我们不行，我们做不到，我们什么都不会啊。”**而这大概也许我们每个人的恐惧吧，面对未知的恐惧？我不知道。

我当时想了想，**难道我连试一试的勇气就没有了吗？我都没有任何需要失去的东西，就这样还不敢尝试吗？**说实话如果现在的自己都这样让我自己讨厌的话，我想未来的我也会如此。

”老师，我试试，我去报名“。

我知道，我是一个脑袋瓜子并不算灵光的人，否则也不会学习着最简单的算法也要看半天，在草稿纸上演算半天，然后改bug又是半天，算下来一天的时光很是短暂。至于我为什么要报考计算机相关专业，大概是我来自农村，想要帮父母分担一点。

2初识比赛

2019广东工业智造创新大赛【赛场二】

下面篇幅比较长都是介绍比赛的背景和赛制的，

可以直接跳转到正文

初识数据

---

2.1大赛概况

人工智能是国家战略性新兴产业。随着广东制造产业信息建设的不断完善，且产业布局较为完整，诞生了一批信息化程度高的工业制造企业，已沉淀积累了一定数据资源。2019年广东省人民政府联合阿里巴巴集团共同启动“广东工业智造创新大赛”，聚焦布匹疵点智能识别和面料剪裁利用率优化，旨在通过数据开放召集全球众智，将重点围绕工业制造大数据展开，以落地为导向，聚集全球顶级人才，发掘全球先进的智能制造应用成果，推动人工智能技术在广东纺织行业的探索与发展，用技术驱动广东智能制造产业转型升级和变革发展。

面料切割利用率的提升是纺织行业长期追求的目标。如何提升面料切割利用率，既是企业生产精益化的难点，也是痛点。在切割之前，需要确定多个零件在面料上的位置和角度，再充分利用零件在形状上的互补特征，对零件排布的方式进行优化。面料切割问题的特性，是零件存在多种尺寸、形状，比如用作衬衫制作的袖子、后背等零件，用来切割的布匹本身存在多类瑕疵，如破洞、折皱、漏纱等，在排版中需要避开。此外，某些订单，对零件存在个性化排版需求，因此在下料环节中，需要依照订单要求进行排版下料。当前纺织行业布匹原材料的成本占到40%左右，价值较高。

本赛场聚焦面料剪裁利用率优化，要求选手研究开发高效可靠的算法，在较短时间范围内计算获得高质量可执行的排版结果，减少切割中形成的边角废料，提升面料切割利用率，减少计划时间、提高工作效率和避免人工计算的失误，提升价值降低成本。

---

2.2赛程安排

因为仅仅参加了初赛的比赛，这里只说明初赛的安排。

初赛（8月19日-9月21日，****UTC+8****）

1. 报名成功后，参赛队伍通过天池平台下载数据（8月15日10:00开放下载），本地调试算法，在线提交结果。参赛队伍在一次评测周期内多次提交结果，新结果版本将覆盖旧版本。参赛地点不限。
2. 比赛提供建模数据集，供参赛选手建立排版优化算法模型；提供评测程序，供评测参赛选手提交的建模数据的排版结果，并给出选手成绩排名。
3. 初赛评测（A榜）：8月19日-9月20日。用提供的建模数据，提交排版结果，系统每天进行1次评测和排名，评测开始时间为当天10:00，按照评测指标从高到低进行排序，定时更新排行榜；排行榜将选择参赛队伍在本阶段的历史最优成绩进行排名展示。
4. 实名认证：报名选手要求实名参赛，完成实名认证。截止9月20日10:00，未按要求完成实名认证队伍，将被取消复赛参赛资格。（实名认证入口：天池网站-个人中心-认证-支付宝实名认证）
5. 初赛结束，要求TOP100团队提交代码审核，代码提交截止时间为9月23日12:00。组委会将进行审核，剔除不符合比赛规则的参赛队伍，晋级空缺名额后补。初赛成绩排名前100名且通过支付宝实名认证的参赛队伍将进入复赛。
   【初赛赛制更新：1）9月21日初赛增加6次评测和排名，评测时间为10:00、12:00、14:00、16:00、18:00、20:00。2）9月20日已产出成绩的队伍如在9月21日成绩被挤出TOP100之外，只要完成实名认证并通过代码审核，依旧具备复赛资格。】

---

2.3参赛对象

大赛面向全社会开放，个人、高等院校、科研单位、企业、创客团队等人员均可报名参赛，组队上限3人。
注：
1）大赛组织机构单位中涉及题目编写、数据接触的人员禁止参赛；
2）阿里云员工和赛事合办单位参赛，可参与排名，但不参与评奖及领取奖金。

老实说，看到这里心里发虚啊，参赛对象范围也太大了！！！

2.4赛题

本赛场聚焦面料剪裁利用率优化，要求选手研究开发高效可靠的算法，在较短时间范围内计算获得高质量可执行的排版结果，减少切割中形成的边角废料，提升面料切割利用率，减少计划时间、提高工作效率和避免人工计算的失误，提升价值降低成本。

在规则面料的情况下，满足零件旋转角度、零件最小间距、最小边距的约束，解决以下两类问题：

初赛赛题：基于所给零件，进行面料排版加工，耗料长度最短，面料利用率最高；

复赛赛题：在问题一的基础上，避开瑕疵区域面料加工，耗料长度最短，面料利用率最高。

2.5竞赛数据及约束说明

本次大赛针对初赛赛题、复赛赛题各提供了2个批次的建模数据，含：面料数据表、零件数据表。

数据文件夹内包括：

• 批次1零件数据
• 批次1面料数据
• 批次2零件数据
• 批次2面料数据
• readme：数据的基本介绍

数据均以csv文件形式提供，编码格式为utf-8。
初赛建模数据将于8月15日提供下载，复赛建模数据将于9月24日提供下载。

2.6数据说明

1）零件数据

编号	列名	说明	示例
1	下料批次号	Primary key	L0001
2	零件号	Primary key	s000001
3	数量		1
4	外轮廓		[[1420.0, 5998.6], [1420.0, 6062.8], [2183.1, 6062.8],[2183.1, 5998.6], [1420.0, 5998.6]]
5	允许旋转角度	逆时针旋转角度	0,90,180,270
6	面料号		M0001

注：外轮廓曲线数据均离散化为点坐标序列；所有尺寸的单位为毫米(mm).

2）面料数据说明

编号	列名	说明	示例
1	面料号	Primary key	M0001
2	面料规格	规则（矩形）面料，长度*宽度（单位：mm）	10000*100
3	瑕疵区域	瑕疵均为圆形区域，标注方式为圆形中心、圆形半径。 比如[[2000,400],80]，即圆形中心坐标点为[2000,400]，半径为80。坐标系的原点为面料的左下角（参考“约束说明“第（7）条说明）	[ [[2000,400],80], [[1000,1200],50], ⋯ ]
4	零件间最小间距		5
5	最小边距		10

注：瑕疵区域均为圆形；所有尺寸的单位为毫米(mm)。

2.7约束说明

排样规则

1）排版的零件不能超出面料的可行区域；

2）排版零件互不重叠；

3）零件按批次，在同一面料上排版；

4）面料可能存在多个长宽度规格，如宽度为900mm、1000mm等、长度为10000mm、12000mm等；

5）允许用户设置切边预留量，如面料四边各预留5mm（最小边距）；切割零件间预留量5mm（最小间距）；


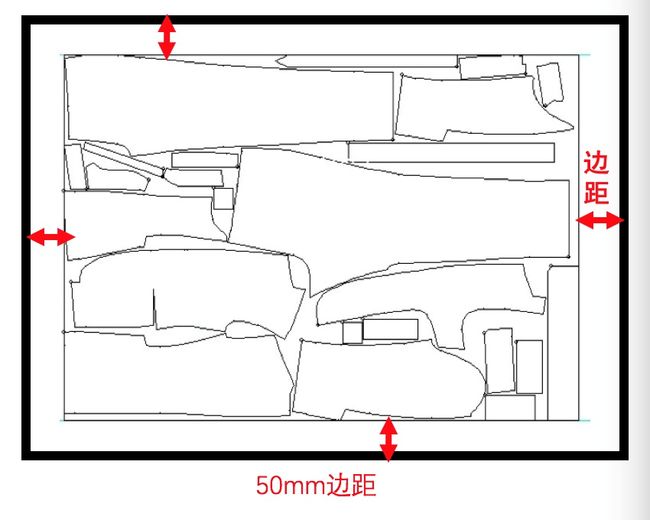
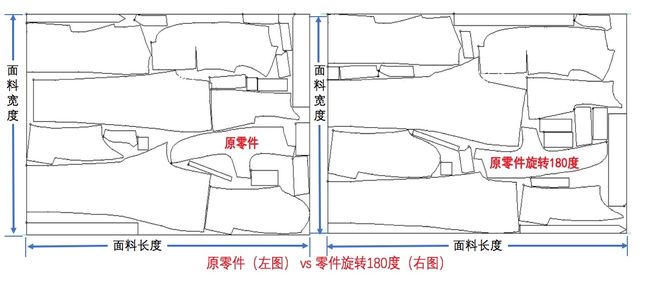
6）某些零件存在旋转角度上的要求，比如零件纹理方向必须保持一致；旋转角度为0表示，零件不允许发生旋转，必须原样放在面料上，面料的放置方向为面料窄边（宽度）在垂直方向，面料宽边（长度）在水平方向；旋转角度为90表示允许零件逆时针旋转90度。

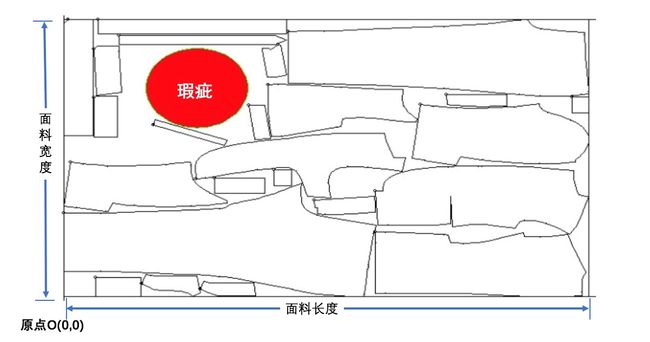
7）切割零件需要避开面料上的瑕疵，瑕疵均为圆形区域，标注方式为圆形中心、圆形半径，坐标系的原点为面料的左下角（参考“数据说明”第（2）条“面料数据说明”），面料的放置方向为面料窄边（宽度）在垂直方向，面料宽边（长度）在水平方向；瑕疵与零件间间距视同零件间间距，即，如果零件间间距（最小距离）为5mm，零件与瑕疵的间距（最小距离）也为5mm。

2.8评估指标

初赛（A榜）:总分=（0.5批次1面料利用率+0.5批次2面料利用率）100总分=（0.5∗批次1面料利用率+0.5∗批次2面料利用率）∗100
复赛（B榜）:总分=（0.5批次1面料利用率+0.5批次2面料利用率）100总分=（0.5∗批次1面料利用率+0.5∗批次2面料利用率）∗100
复赛（C榜）:总分= 权重参数1面料利用率-权重参数2计算时间分值总分=权重参数1∗面料利用率−权重参数2∗计算时间分值
决赛总分=0.3B榜成绩+0.4C榜成绩+0.3现场答辩决赛总分=0.3∗B榜成绩+0.4∗C*榜成绩+0.3∗现场答辩

• 面料利用率=一个批次包含的零件总面积/消耗的面料总面积（消耗面料长度*面料宽度）

  解释：用于衡量布匹原材料的利用情况，即使用长度越短、耗料越少的面料满足全部订单的生产，则切割利用率越高。

• 计算时间分值=f(一个批次排版的平均计算时间)

  解释：计算时间越长，对应的计算时间分值呈阶梯的方式上升，具体对应如下表。

计算时间（分钟）	计算时间分值
(0,5)	0
[5,20)	1
[20,60)	3
[60,180)	5
180以上	20

• 权重参数如下。
  权重参数1=100.0
  权重系数2=1.0

2.9提交说明

2.10排版结果提交

请将提供的生产订单，给出在给定面料、零件条件下的切割排版结果，在满足约束条件的基础上通过算法计算得出目标函数值（见“评估指标”）最大的排版优化方案，并用时较短。

编程语言不限，建议使用Python、Java 、C#、C++。

排版结果，以面料左下角作为x-y坐标原点，提供排版输出。计算结果以csv文件形式提交，编码格式为utf-8，文件名为选手昵称+下划线+排版批次号+下划线+目标函数值（小数点后3位），例如选手绿洲520的成绩是0.876，那么文件名就是“绿洲520_ L0001_876.csv”。比赛阶段提供2个批次的建模数据，则需要提交2个csv文件，并打包成一个zip文件提交，见“ 附注：代码规范参考”。

计算结果数据输出格式：

下料批次号	L0001
零件号	s000001
面料号	M0001
零件外轮廓线坐标	[[1420.0,5998.6],[1420.0,6062.8],[2183.1,6062.8],[2183.1,5998.6],[1420.0,5998.6]]

以下图中两个排版零件为例：

2.11代码审核提交

初赛
初赛结束，要求TOP100团队提交代码审核，代码提交截止时间为9月22日22:00。

复赛
复赛结束，组委会将要求B榜TOP20参赛队伍提交代码审核，并进行最优提交成绩的模型审核。最优提交成绩审核采用docker容器镜像的提交方式，由选手提交打包好的模型容器镜像来运行得出排版结果。源代码提交截止时间：10月27日12:00，部署时间：10月25日-11月1日12:00。

复赛B榜复现和C榜测试提供的线上环境配置为16核64G，实例规格ecs.g6.4xlarge，处理器型号Intel Xeon(Cascade Lake)Platinum 8269。

复赛B榜复现和C榜测试会限定一定计算时间，需在一定计算内跑出结果，如3小时（具体时间复赛公布）。超出时间没有结果将计为没有成绩。

对于未提交、复现未成功（没有结果，或结果误差太大）、或代码审核不通过的队伍，将取消决赛资格和比赛奖励。同时取消复赛排行榜成绩。

需提交：
1、 源代码 ，源代码需要留好测试接口，如提供数据说明中定义的零件数据及面料数据格式的csv文件，调用算法代码后，能够输出如1、中定义的排版结果csv文件及排版利用率。
2、 技术文档（包括使用帮助文档，测试文档等）
3、 提交代码需参照“代码规范文档”，“代码规范文档”将于8月25日提供。

2.12计算时间提交

初赛A榜、复赛B榜阶段请填写机器配置和每个批次排版的计算完成时间（配置描述如：普通PC服务器，2颗10核CPU，30G内存）；复赛C榜和决赛阶段由组织方提供统一的计算资源（相同的机器配置，如16核，64G）。

2.13注意事项

1. 不允许使用商业求解器。
2. 计算正确无误，满足约束条件。
3. 目标函数值大，请填写面料利用率目标函数值。
4. 计算速度快，初赛A榜、复赛B榜阶段请填写机器配置和每个批次排版的计算完成时间（配置描述如：普通PC服务器，2颗10核CPU，30G内存）；复赛C榜和决赛阶段由组织方提供统一的计算资源（相同的机器配置）。
   注：计算时间按照阶梯函数的方式进行相应的罚分计算
5. 如果抽查发现参赛队伍有造假、作弊、雷同等行为，将取消该队伍的参赛资格及奖励。
6. 参考资料：https://svgnest.com/

3初识数据

3.1观察图形

下载完数据之后，我们首先要做的肯定是观察数据，然后把图形绘制出来。

数据详情：

这是一个图形的轮廓坐标点。

从这里可以看出来数据量真的很大。

3.2提取数据与数据清洗工作

我们知道python读取数据的时候是按照字符串的形式读取的，而我们目标是点对的形式出现的。

对于这组数据肯定我们希望得到以下点对：

X	Y
14000.0	10000.0
14000.0	1200.0
13930.0	1200.0
13930.0	1000.0
14000.0	1000.0

如何提取到这些点呢?,我们首先寻找一下不需要的字符。

1、开头的中括号。

2、重复出现的”], [“。

3、数字之间的间隔”， “。

解决方法是：去掉两边的”[["和“]]”然后我们就可以发现规律了，中间总是有“], [”。我们可以用split（）函数处理，然后就剩下3中的情况，再用一次split（）**函数就可以解决了。

请看代码：

import csv


# 提取数据
data_file = open("L0002_lingjian.csv", "r", encoding="utf-8")
data = csv.reader(data_file)
# data_file.close()
# 提取零件外形点
points_sets = []
for item in data:
    if data.line_num == 1:
        continue
    points_sets.append(item[3][1:-1])

for i in range(len(points_sets)):
    points_sets[i] = points_sets[i][1:-1].split('], [')

那么points_sets代表什么？

代表了所有图形的坐标点集，例如points_sets[19]代表了第20个图形的点对。

print(points_sets[19])
['14000.0, 2000.0', '13930.0, 2000.0', '13930.0, 1800.0', '14000.0, 1800.0', '14000.0, 2000.0']

后续如果我们想要调用其中的点的话。

例如这个图形第一个点可以用下面代码表示。

x, y = points_sets[19][0].split(', ')

就可以得到坐标点x和y。

3.3绘制图形

我们首先导入一组点，绘制出来看看实际的效果图。

示例为第一图形的点：

p1 = []
p2 = []
for point_x_y in points_sets[0]:
    # print(point_x_y)
    x, y = map(float, point_x_y.split(','))
    p1.append(x)
    p2.append(y)
plt.plot(p1, p2)
plt.draw()
plt.savefig("image2.png")
# plt.pause(10) 展示图片10秒
plt.close()

我们可以得到以下信息：

• 图形是不平整的。
• 图形可以能是奇奇怪怪的形状。
• 可能存在矩形，三角形规则图形。

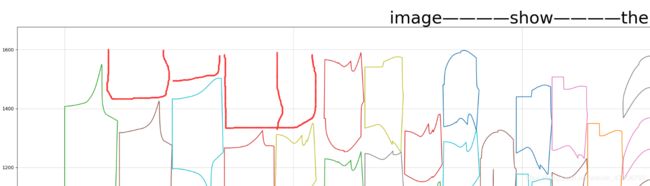
接下来我们绘制所有的图形！！！超级大的版面！！

plt.figure('Draw', figsize=(40, 20))
plt.title("image————show", size=36)
plt.xlabel("X", size=36)
plt.ylabel("Y", size=36)
plt.grid(alpha=0.4)
for points in points_sets:
    p1 = []
    p2 = []
    for point_x_y in points:
        # print(point_x_y)
        x, y = map(float, point_x_y.split(','))
        p1.append(x)
        p2.append(y)
    plt.plot(p1, p2)
plt.draw()
plt.savefig("image1.png")
# plt.pause(10) 展示图片10秒
plt.close()

可能图形比较多，看起来比较模糊。

但我们仍然能够知道大致的图形轮廓。

不规则！！

感觉太难了QAQ。

3.4凸包多边形最小外切矩形算法

这么复杂的图形，怎么排版，直接排肯定是比较难的，我们引入凸包多边形最小外切矩形的概念。

那么什么是凸包多边形最小外切矩形呢？

简单来说就是找到一个最小的矩形，能够把该图形完全覆盖

例如：

内部是图形，外边矩形是最小外切矩形。（图画的贼丑，不要介意）

类似这样的矩阵就是我们接下来要求得的。

求法呢，这里有旋转卡壳算法。

但是呢，我一开始并没有想太复杂，那就没有用这个方法。QAQ。

我们完全可以接住坐标点来进行。

图像分析：

文字分析：

假定我们的图形都是垂直方向上的，那么我们如何得到这个矩形的宽呢？肯定是图形上面的切线减去下面的切线。我们假定切线是水平的，那么我们如何求出切线呢 。其实就是最高点和最低点。然后我们通过最高点的竖直坐标（y1）减去最低点的竖直坐标（y2），可以求得最小矩形的宽。同理我们可以求出最右点和最左点，通过最右点的水平坐标（x1）减去最左点的水平坐标（x2）可以得到最小矩形的长。

具体实现方法：

rectangles = []
plt.grid(alpha=0.4)
for points in points_sets:
    p1 = []
    p2 = []
    for point_x_y in points:
        # print(point_x_y)
        x, y = map(float, point_x_y.split(','))
        p1.append(x)
        p2.append(y)
    # 计算矩形特征
    rectangle = {'long_max': max(p1), 'long_min': min(p1), 'wide_max': max(p2),
                 'wide_min': min(p2), 'points': points, 'floor': 0}
    rectangle['length'] = rectangle['long_max'] - rectangle['long_min']
    rectangle['width'] = rectangle['wide_max'] - rectangle['wide_min']
    rectangle['area'] = rectangle['length'] * rectangle['width']
    rectangles.append(rectangle)
    # 计算之后存入到矩形特征列表

这样我们可以得到任何图形的**长，宽，最高点，最低点，最右点和最左点**。后面的其它矩形的特征也会添加到这个里面，也就是我们知道导出rectangle字典，就可以得到任何想要的特征。（感觉还不错）

3.5矩形排序&组合

这种方法是在论文上看到的，具体哪个论文听不清楚了。先排大的矩形，然后在排小的矩形，按照一层一层的排列，可以增大利用率。

于是我们得到了两种排法：

按照长度，一层一层排：

按照宽度，一层一层排：

排序代码：

def cmp(value1, value2):
    # 按宽度排
    if value1['width'] == value2['width']:
        return value2['length'] - value1['length']
    return value2['width'] - value1['width']


def cmp2(value1, value2):
    # 按长度排
    if value1['length'] == value2['length']:
        return value2['width'] - value1['width']
    return value2['length'] - value1['length']

# 排序，长度，排宽度
rectangles.sort(key=functools.cmp_to_key(cmp))

这里我们引入了一个functools库来解决复杂排序问题。

重点来了！！！怎么进行组合呢？上面的排序只是解决了最小包络矩形的优先问题，接下来的问题就是如何才能够按照层次进行组合呢？一层一层还是有很多细节的。

我们按照层次排序无疑是通过坐标点的移动。

我们先看一下初始的排版。

可以看出来，所有的坐标点都是在这一张版图上排列。

所以，我们想要组合图形，就必须设置到坐标点的移动。

下面是手绘演示：

1、绘制出大致的图形。

2、假定我们竖直组合，移动第一个图形。

现在的问题是，我们应该如何移动点呢？

观察下面的移动方式

我们是不是可以得出，原来是这个图形的所有点集通过x与y的所有点坐标移动可以得到。

# 移动x坐标
x -= d1

# 移动y坐标
y -= d2

3、我们接着继续移动图形。

我们可以发现，此时，我们并不能够对y坐标进行相减操作。

而是坐标要进行y坐标的相加。

y += d2

然后我们其实可以发现，这个d2我们可以不取绝对值，然后每次都是第二个图形的最小的y值减去第一个图形的最小y值。第二个图形移动就是坐标y减去d2.

d2 = second_min_y - first_min_y
# 进行坐标变换
y -= d2

4、同理，我们会出现，第二个图形在第一个左边的情况。

如图：

我们也可以通过第二个图形的最左边减去第一个图形的最左边得到非绝对值d1。

d1 = second_min_x - first_min_x
# 进行坐标变换
x -= d1

今已创业过半，丞相可以安矣

5、解决一层放不下的问题。

此时已经超出了允许的边界，那就不能放了，只能放在下一层，然后从第二层开始放图形。

当然从二层开始的时候，左边界也要进行更新。

3.6核心代码（未维护）

# 排序，长度，排宽度
rectangles.sort(key=functools.cmp_to_key(cmp))

# 进行堆叠 没有维护
long_left, long_right, wide_height, wide = 0, 0, rectangles[0]['width'], 0
max_long, max_wide = 0, 0
floor = 1
for i in range(len(rectangles)):
    if long_right + rectangles[i]['length'] < long_cloth:
        long_right += rectangles[i]['length']
        rectangles[i]['floor'] = floor
    else:
        wide = wide_height
        wide_height += rectangles[i]['width']
        long_left = 0
        long_right = rectangles[i]['length']
        floor += 1
    # 改动点坐标
    points = []
    for point_x_y in rectangles[i]['points']:
        x, y = map(float, point_x_y.split(','))
        x -= rectangles[i]['long_min'] - long_left
        y -= rectangles[i]['wide_min'] - wide
        points.append([x, y])
    rectangles[i]['new_points'] = points
    long_left = long_right
    max_long = max(max_long, long_right)
    max_wide = max(max_wide, wide_height)
# 绘制图片
plt.figure('Draw', figsize=(40, 20))
plt.title("image————show————the wide", size=36)
plt.xlabel("X", size=36)
plt.ylabel("Y", size=36)
plt.grid(alpha=0.4)
for rectangle in rectangles:
    p1 = []
    p2 = []
    for point_x_y in rectangle['new_points']:
        p1.append(point_x_y[0])
        p2.append(point_x_y[1])
    plt.plot(p1, p2)
plt.draw()
plt.savefig("image2.png")
# plt.pause(10) 展示图片10秒
plt.close()

运行图片结果请看。

排版结果.

4优化提升

4.1层次优化

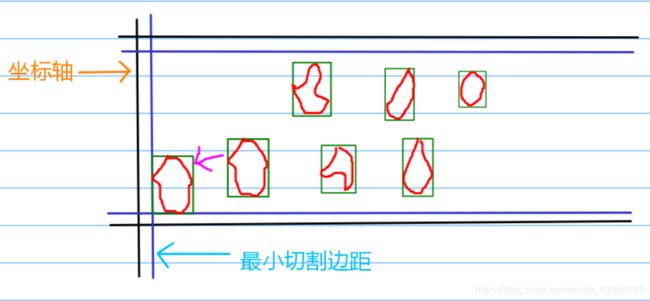
**层次优化**这当然时我自己起的名字，不过挺贴切的。就是一直去维护前面几层，直至到达边界。举个例子，我们在放第三层的时候，首先考虑，第一层是否能够放得下，然后判断第二层是否能够放的下。

如图：

红色圈出的地方就是没有被利用的空间，还是很多的是吧。

思路就是每次放图形的时候，我们首先要判断前面几层是否能够放下。

因此我们也要记录特征。

• floor：记录层级。
• 记录该层的最高点，最低点，最左点，最右点。
• 记录图形的序号。（为了以后提取数据）。
• 是否需要建立新层。
• 长度，宽度。
• 左边点变换！！（好几次都没有变换好，导致出现问题）
• …

这些是比较重要的特征。

4.1.1层次优化代码：

# 长度排序 + 维护
rectangles.sort(key=functools.cmp_to_key(cmp2))
long_left, long_right, wide_height, wide = 0, rectangles[0]['length'], 0, 0
max_long, max_wide = 0, 0
floor = 0
to_test_floor = [{}] * 100
to_test_floor[0] = {'long_right': rectangles[0]['length'],
                    'long_left': 0, 'wide': 0, 'wide_height': 0}
for i in range(len(rectangles)):
    # 维护前面几层
    for floor_ in range(floor + 1):
        if rectangles[i]['width'] + to_test_floor[floor_]['wide_height'] <= wide_cloth:
            to_test_floor[floor_]['wide_height'] += rectangles[i]['width']
            # 改动点坐标
            points = []
            for point_x_y in rectangles[i]['points']:
                x, y = map(float, point_x_y.split(','))
                x -= rectangles[i]['long_min'] - \
                    to_test_floor[floor_]['long_left']
                y -= rectangles[i]['wide_min'] - to_test_floor[floor_]['wide']
                points.append([x, y])
            to_test_floor[floor_]['wide'] = to_test_floor[floor_]['wide_height']
            rectangles[i]['new_points'] = points
            # print("第", i,"个" + "添加到", floor_, "后的高度是", to_test_floor[floor_]['wide'])
            max_long = max(max_long, to_test_floor[floor_]['long_right'])
            max_wide = max(max_wide, to_test_floor[floor_]['wide_height'])
            flag = 1
            break
    else:
        # 建立新层
        long_left, long_right, wide_height, wide = to_test_floor[floor]['long_right'], \
            to_test_floor[floor]['long_right'] + \
            rectangles[i]['length'], 0, 0
        floor += 1
        # 改动点坐标
        points = []
        for point_x_y in rectangles[i]['points']:
            x, y = map(float, point_x_y.split(','))
            x -= rectangles[i]['long_min'] - long_left
            y -= rectangles[i]['wide_min'] - wide
            points.append([x, y])
        rectangles[i]['new_points'] = points
        wide_height = rectangles[i]['width']
        wide = wide_height
        to_test_floor[floor] = {'long_right': long_right,
                                'long_left': long_left, 'wide': wide, 'wide_height': wide_height}
        max_long = max(max_long, long_right)
        max_wide = max(max_wide, wide_height)

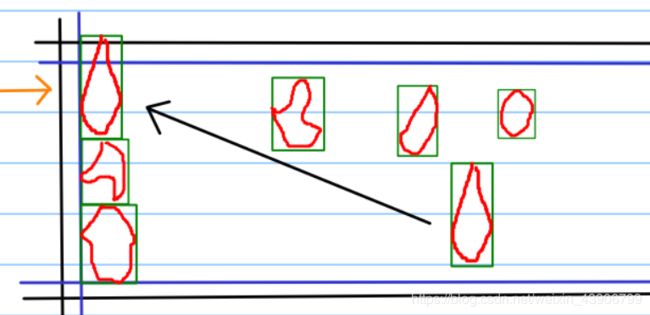
4.1.2层次优化结果展示和对比：

优化后：

优化前：

整张图片：

没有进行层次优化之前的：

可以看出来，差距很显著。

4.2间距优化

什么是间距优化，可能有人会说，你这是在瞎扯！我也不知道有没有这个算法，这是偶然间想到的。QAQ，不说闲话了，我们直接看图分析。

这些距离一看，都是可以往下移动的。emmmm我当时也是这样认为的，同时我也陷入了自我怀疑当中。

• 能移动吗？
• 能吗？
• 真的能移动吗？
• 真的呀？

怎么移动？

可是给的数据都是坐标点，怎么移动，怎么找距离？

“今天就是天王老子来了，他也不能移动！！！”

想起当时我那个时候想破脑袋也没有想出来的办法，于是气呼呼的说出这样的话。

不知道哪一个瞬间，突然get到一个想法，寻找两个图形的最小间距！！。

突然绝的这个想法超级好。当时想法很简单。

找到这个图形的上面的x，和另一个图形下面的x进行求距离运算。

就是这样

然后迫不及待的构建键值对{x：y}.写好程序，生成结果。

但是有的图形重叠了，有的图形间距更大了。

后来发现原因竟然是这个图形的x另一个图形中未必有这个x。

因为图形是根据坐标点构建的。

此方法还需要进行优化。

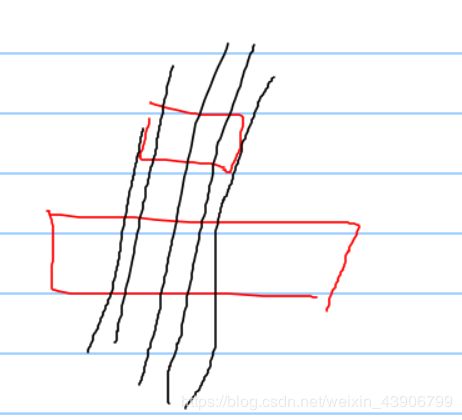
4.2.1坐标点对绘制图形原理

对于绘制封闭图形来说，肯定是每两个连续的点之间进行直线/线段连接。顺时针和逆时针都无所谓，只要是收尾相连接就好。

类似下面的连接方式。

知道这个了之后我们引入下面的优化算法。

4.2.2散点化

什么是散点化？

就是我们人为的增加直线间的点的数量。

那么可以这样进行吗？

我们观察数据：

[[14000.0, 1000.0], [14000.0, 1200.0], [13930.0, 1200.0], [13930.0, 1000.0], [14000.0, 1000.0]]

可以发现精度为0.1.所以我们完全可以执行这样的操作。

• 取两个连续的点（题目给的点是逆序或顺序）
• 拟合直线
• 间距为0.1，进行补充点

我的方法是原始数据先扩大10倍，这样防止了浮点数运算造成的不精确的后果。

4.2.3直线拟合

k = (y_2 - y_1) / (x_2 - x_1)
c = y_1 - k * x_1

4.2.4间距计算方法

基本思路还是和上面的一样，我们变量下面图形的x值，判断上面图形中是否含有x，有的话，则相减。因为下面的图形一定大于上面的图形的宽度（排序算法所决定的）。

判断上面图形是否含有x的原因是这种情况：

然后通过竖直距离的高度差，即可以得到，最小间隔。

间距计算代码

def to_return_dis(points_set):
    height_points = {}
    low_points = {}
    for index in range(len(points_set) - 1):
        if abs(points_set[index][0] - points_set[index + 1][0]) > 1:
            x_1, x_2, y_1, y_2 = \
                points_set[index][0], points_set[index + 1][0], points_set[index][1], points_set[index + 1][1]
            if x_1 > x_2:
                x_1, x_2 = x_2, x_1
                y_1, y_2 = y_2, y_1
            k = (y_2 - y_1) / (x_2 - x_1)
            c = y_1 - k * x_1
            # 精度为1
            for point_x in range(x_1, x_2):
                point_y = int(k * point_x + c)
                if point_x in height_points:
                    height_points[point_x] = max(
                        height_points[point_x], point_y)
                else:
                    height_points[point_x] = point_y
                if point_x in low_points:
                    low_points[point_x] = min(low_points[point_x], point_y)
                else:
                    low_points[point_x] = point_y
    return height_points, low_points

4.3层次维护&间距维护

4.3.1基本思想

基本思想就是想维护层次，然后再维护间距。因为这样我们可以优先安排前面几层。

变量名	变量意义
max_long	记录图形在图纸所能到达的最右边，为计算性能指标做铺垫。
max_wide	记录图形在图纸所能到达的最上边，为计算性能指标做铺垫。
long_left	代表当前放置层的图形左标线。
long_right	代表当前放置层的图形右标线。
wide_height	该层放置图形后的最高点。
wide	该层放置图形前的最高点，需要延迟标记。
floor	记录该图形位于第几层，同时记录最高层

4.3.2代码实现

for i in range(len(rectangles)):
        flag_j = 0
        for j in range(len(to_test_data)):
            if to_test_data[j]['wide_height'] + rectangles[i]['width'] + 100 <= wide_cloth:
                to_test_data[j]['wide_height'] += rectangles[i]['width'] + 100
                rectangles[i]['floor'] = floor
                wide_height = to_test_data[j]['wide_height']
                wide = to_test_data[j]['wide']
                long_left = to_test_data[j]['long_left']
                long_right = to_test_data[j]['long_right']
                flag_j = j
                break
        else:
            long_left = to_test_data[-1]['long_right'] + 50
            long_right = rectangles[i]['length'] + long_left
            wide_height = rectangles[i]['width']
            wide = 0
            floor += 1
            flag_j = floor
            to_test_data.append(to_return_temp_data(
                long_left, long_right, 0, wide_height))
        # 改变点-
        points = to_change_points(i, 0)
        rectangles[i]['height_points'], rectangles[i]['low_points'] = to_return_dis(
            points)
        rectangles[i]['new_points'] = points

        the_min_dis = 0
        # 维护信息
        if wide != 0:
            dis = 1 << 30
            # 初始化一个较大值
            # 维护每一层的最后一个图形
            for key1 in rectangles[i]['low_points'].keys():
                # 遍历现在图像的x值,如果x同样在上一个图像,求出差值
                if key1 in rectangles[to_test_data[flag_j]['flag_i']]['height_points']:
                    dis = min(dis, rectangles[i]['low_points'][key1] -
                              rectangles[to_test_data[flag_j]['flag_i']]['height_points'][key1])
            dis -= 100
            if dis != 1 << 30:
                # print("第", i + 1, "向第", i, "个图像移动的距离是", dis)
                the_min_dis = dis
                # 维护点,像下边相切,用原始点计算加上向下的距离对,别的写法纠错,我可迷.
                points = to_change_points(i, dis)
                # 更新该图形对应的x最高点和最低点，以及所有的点
                rectangles[i]['height_points'], rectangles[i]['low_points'] = to_return_dis(
                    points)
                rectangles[i]['new_points'] = points
                wide_height -= the_min_dis
        # 延迟标记下边的宽
        wide = wide_height
        to_test_data[flag_j] = to_return_temp_data(
            long_left, long_right, wide, wide_height)
        to_test_data[flag_j]['flag_i'] = i
        max_long = max(max_long, long_right)
        max_wide = max(max_wide, wide_height)

4.4性能指标计算

4.4.1面积计算-向量叉乘

题目明确的说明了给出的数据是逆序或者顺序的，所以我们就可以最后取绝对值计算出来他们的面积。

有一点要明确的是，每一次使用叉乘求面积，不能加绝对值，因为每一步叉乘求面积求得的是有向面积，将所有的有向面积加和所求的就是该多边形的面积，这种方法不仅适用于凸多边形，同时也适用于凹多边形。

4.4.2代码实现

sum_area = 0
for points in points_sets:
    area = 0
    for i in range(len(points) - 1):
        x1, y1 = map(float, points[i].split(','))
        x1, y1 = int(10 * x1), int(10 * y1)
        x2, y2 = map(float, points[i + 1].split(','))
        x2, y2 = int(10 * x2), int(10 * y2)
        area += x1 * y2 - x2 * y1
    area /= 2
    sum_area += abs(area)

4.5最终版结果展示

因为题目要求零件直接的间距。

4.6比赛成绩

因为下面是真实名字所以没有展出。

5后记与全部代码

5.1后记

怎么说呢，第一次参加天池的比赛，开始的时候其实很害怕，因为自己什么都不会，觉得自己肯定不行，其实也就是有一点自卑吧，想想自己大一也没干什么特别的事情，参加ACM，刷着OJ，学着基本的算法。回想起大一刚刚开学的那个国庆节，和室友一起从早到晚就在刷着OJ，7天刷了100道题目，倒是把基础的语法知识都给掌握了，想起那时候我们熬夜到凌晨2点刷题，然后说睡觉吧。那个事情痛苦并快乐着，大一自己学校的OJ刷了500+道的基本的算法题，也跟着学校ACM队寒假集训，暑假集训。不知道有没有刷够1000+的题目，刷的题目大多也忘记了，现在只留下了思维方式。

大学，真的不是想象当中的轻松，这次比赛可能是带给我了极大的鼓舞和自信，也就是精神上的升华。当时为了给比赛留下时间调试代码，中午匆匆的吃完饭，就带者自己的电脑去自习室，结果学长和学姐们刚刚从自习室离开。

最紧张与失落的应该是提交代码的前天晚上。我知道明天就要结束比赛了，明天最后一次评测，这是最后一次提交，检查了数次，最后提交了，但是还是在晚上又悄悄爬下床来改bug！！！数据忘了除以10了。

提交结果很快出来了，返回的结果竟然是布料重叠！！

当时内心倒是很平静的，但是挺失落。

回到寝室，又最后一次看看哪里出现了问题，想着，比赛可以不参加，可以不得奖，但是对待自己的态度还是要有的，看到比赛规则写者，零件之间的间距问题。

原来是这里出错了，改完bug，至少对得起自己。然后无心的提交了一次。

后来等到比赛完全结束，我才知道我初赛有成绩。也没有什么遗憾的地方，感谢主办方给我一次评测的机会，感谢拼命的自己

5.2代码

import matplotlib.pyplot as plt
import csv
import functools


def cmp(value1, value2):
    # 按宽度排
    if value1['width'] == value2['width']:
        return value2['length'] - value1['length']
    return value2['width'] - value1['width']


def cmp2(value1, value2):
    # 按长度排
    if value1['length'] == value2['length']:
        return value2['width'] - value1['width']
    return value2['length'] - value1['length']


def cmp3(value1, value2):
    # 零件号排序
    return int(value1['lingjianhao'][1:]) - int(value2['lingjianhao'][1:])


def to_return_dis(points_set):
    height_points = {}
    low_points = {}
    for index in range(len(points_set) - 1):
        if abs(points_set[index][0] - points_set[index + 1][0]) > 1:
            x_1, x_2, y_1, y_2 = \
                points_set[index][0], points_set[index +
                                                 1][0], points_set[index][1], points_set[index + 1][1]
            if x_1 > x_2:
                x_1, x_2 = x_2, x_1
                y_1, y_2 = y_2, y_1
            k = (y_2 - y_1) / (x_2 - x_1)
            c = y_1 - k * x_1
            # 精度为1
            for point_x in range(x_1, x_2):
                point_y = int(k * point_x + c)
                if point_x in height_points:
                    height_points[point_x] = max(
                        height_points[point_x], point_y)
                else:
                    height_points[point_x] = point_y
                if point_x in low_points:
                    low_points[point_x] = min(low_points[point_x], point_y)
                else:
                    low_points[point_x] = point_y
    return height_points, low_points


def to_solve(data, cloth_data):
    # 提取布料长度宽度
    long_cloth, wide_cloth = 0, 0
    for item in cloth_data:
        if cloth_data.line_num == 1:
            continue
        long_cloth_float, wide_cloth_float = map(float, item[1].split('*'))
        long_cloth, wide_cloth = int(
            long_cloth_float * 10), int(wide_cloth_float * 10)
    # 提取零件外形点
    points_sets = []
    lingjianhao = []
    for item in data:
        if data.line_num == 1:
            continue
        lingjianhao.append(item[1])
        points_sets.append(item[3][1:-1])

    for i in range(len(points_sets)):
        points_sets[i] = points_sets[i][1:-1].split('], [')

    # 计算面积
    sum_area = 0
    for points in points_sets:
        area = 0
        for i in range(len(points) - 1):
            x1, y1 = map(float, points[i].split(','))
            x1, y1 = int(10 * x1), int(10 * y1)
            x2, y2 = map(float, points[i + 1].split(','))
            x2, y2 = int(10 * x2), int(10 * y2)
            area += x1 * y2 - x2 * y1
        area /= 2
        sum_area += abs(area)

    # 绘图
    # 求最大矩形的长和宽

    rectangles = []
    lingjian_cnt = 0
    for points in points_sets:
        p1 = []
        p2 = []
        for point_x_y in points:
            # print(point_x_y)
            x, y = map(float, point_x_y.split(','))
            x, y = int(10 * x), int(10 * y)
            p1.append(x)
            p2.append(y)
        # 计算矩形特征
        rectangle = {'long_max': max(p1),
                     'long_min': min(p1),
                     'wide_max': max(p2),
                     'wide_min': min(p2),
                     'points': points,
                     'floor': 0,
                     'lingjianhao': lingjianhao[lingjian_cnt]
                     }
        lingjian_cnt += 1
        rectangle['length'] = rectangle['long_max'] - rectangle['long_min']
        rectangle['width'] = rectangle['wide_max'] - rectangle['wide_min']
        rectangle['area'] = rectangle['length'] * rectangle['width']
        rectangle['height_points'] = {}
        rectangle['low_points'] = {}
        rectangles.append(rectangle)
        # 计算之后存入到矩形特征列表
    # 长度排序
    rectangles.sort(key=functools.cmp_to_key(cmp2))
    long_left, long_right, wide_height, wide = 0, rectangles[0]['length'], 0, 0
    max_long, max_wide = 0, 0
    floor = 0

    def to_change_points(index, dist):
        new_points = []
        for point in rectangles[index]['points']:
            point_x, point_y = map(float, point.split(','))
            point_x = int(point_x * 10)
            point_y = int(point_y * 10)
            point_x -= rectangles[index]['long_min'] - long_left
            point_y -= rectangles[index]['wide_min'] - wide + dist
            new_points.append([point_x, point_y])
        return new_points

    def to_return_temp_data(long_left_, long_right_, wide_, wide_height_):
        temp_data = {'long_left': long_left_, 'long_right': long_right_,
                     'wide': wide_, 'wide_height': wide_height_, 'flag_i': 0}
        return temp_data

    to_test_data = [to_return_temp_data(
        long_left, long_right, wide, wide_height)]
    for i in range(len(rectangles)):
        flag_j = 0
        for j in range(len(to_test_data)):
            if to_test_data[j]['wide_height'] + rectangles[i]['width'] + 100 <= wide_cloth:
                to_test_data[j]['wide_height'] += rectangles[i]['width'] + 100
                rectangles[i]['floor'] = floor
                wide_height = to_test_data[j]['wide_height']
                wide = to_test_data[j]['wide']
                long_left = to_test_data[j]['long_left']
                long_right = to_test_data[j]['long_right']
                flag_j = j
                break
        else:
            long_left = to_test_data[-1]['long_right'] + 50
            long_right = rectangles[i]['length'] + long_left
            wide_height = rectangles[i]['width']
            wide = 0
            floor += 1
            flag_j = floor
            to_test_data.append(to_return_temp_data(
                long_left, long_right, 0, wide_height))
        # 改变点-
        points = to_change_points(i, 0)
        rectangles[i]['height_points'], rectangles[i]['low_points'] = to_return_dis(
            points)
        rectangles[i]['new_points'] = points

        the_min_dis = 0
        # 维护信息
        if wide != 0:
            dis = 1 << 30
            # 初始化一个较大值
            # 维护每一层的最后一个图形
            for key1 in rectangles[i]['low_points'].keys():
                # 遍历现在图像的x值,如果x同样在上一个图像,求出差值
                if key1 in rectangles[to_test_data[flag_j]['flag_i']]['height_points']:
                    dis = min(dis, rectangles[i]['low_points'][key1] -
                              rectangles[to_test_data[flag_j]['flag_i']]['height_points'][key1])
            dis -= 100
            if dis != 1 << 30:
                # print("第", i + 1, "向第", i, "个图像移动的距离是", dis)
                the_min_dis = dis
                # 维护点,像下边相切,用原始点计算加上向下的距离对,别的写法纠错,我可迷.
                points = to_change_points(i, dis)
                # 更新该图形对应的x最高点和最低点，以及所有的点
                rectangles[i]['height_points'], rectangles[i]['low_points'] = to_return_dis(
                    points)
                rectangles[i]['new_points'] = points
                wide_height -= the_min_dis
        # 延迟标记下边的宽
        wide = wide_height
        to_test_data[flag_j] = to_return_temp_data(
            long_left, long_right, wide, wide_height)
        to_test_data[flag_j]['flag_i'] = i
        max_long = max(max_long, long_right)
        max_wide = max(max_wide, wide_height)
    rectangles.sort(key=functools.cmp_to_key(cmp3))
    for i in range(len(rectangles)):
        points = []
        for point_x_y in rectangles[i]['new_points']:
            points.append([point_x_y[0] / 10, point_x_y[1] / 10])
        rectangles[i]['new_points'] = points
    # print("图形总面积是", sum_area / 100)
    # print("最小覆盖矩形长是", max_long / 10, "最小覆盖矩形宽是", max_wide / 10)
    # print("布匹的长是", long_cloth / 10, "布匹的宽是", wide_cloth / 10)
    print("面料利用率是", sum_area / max_long / max_wide * 100, "%")
    return rectangles


# 提取数据 1
data_file = open(r"..\data\L0002_lingjian.csv", "r", encoding="utf-8")
data = csv.reader(data_file)
cloth_data_file = open(r"..\data\L0002_mianliao.csv", "r", encoding="utf-8")
cloth_data = csv.reader(cloth_data_file)

# 调用算法
rectangles = to_solve(data, cloth_data)

with open(r"..\submit\DatasetA\星夜_ai_L0002_694.csv", "w", encoding="utf-8", newline="") as csv_file:
    write = csv.writer(csv_file)
    # 写入标题
    write.writerow(['下料批次号', '零件号', '面料号', '零件外轮廓线坐标'])
    # 写入多行data
    for points in rectangles:
        write.writerow(['L0002', points['lingjianhao'],
                        'M0002', points['new_points']])

# 提取数据 2
data_file = open(r"..\data\L0003_lingjian.csv", "r", encoding="utf-8")
data = csv.reader(data_file)
cloth_data_file = open(r"..\data\L0003_mianliao.csv", "r", encoding="utf-8")
cloth_data = csv.reader(cloth_data_file)

# 调用算法
rectangles = to_solve(data, cloth_data)

with open(r"..\submit\DatasetA\星夜_ai_L0003_705.csv", "w", encoding="utf-8", newline="") as csv_file:
    write = csv.writer(csv_file)
    # 写入标题
    write.writerow(['下料批次号', '零件号', '面料号', '零件外轮廓线坐标'])
    # 写入多行data
    for points in rectangles:
        write.writerow(['L0003', points['lingjianhao'],
                        'M0003', points['new_points']])