算法竞赛专题解析(12):DP优化(2)--斜率(凸壳)优化
本系列文章将于2021年整理出版,书名《算法竞赛专题解析》。
前驱教材:《算法竞赛入门到进阶》 清华大学出版社
网购:京东 当当 作者签名书
如有建议,请加QQ 群:567554289,或联系作者QQ:15512356
文章目录
- 1. 把状态方程变换为平面的斜率问题
- 2. 求一个dp[i]
- 3. 求所有的dp[i]
- 4. 例题
- 5. 习题
有一类DP状态方程,例如:
d p [ i ] = m i n { d p [ j ] − a [ i ] ∗ d [ j ] } dp[i] = min\{dp[j] - a[i]*d[j]\} dp[i]=min{dp[j]−a[i]∗d[j]} 0 ≤ j < i , d [ j ] ≤ d [ j + 1 ] , a [ i ] ≤ a [ i + 1 ] 0≤j
它的特征是存在一个既有 i i i又有 j j j的项 a [ i ] ∗ d [ j ] a[i]*d[j] a[i]∗d[j]。
编程时,如果简单地对 i i i和 j j j循环,复杂度是 O ( n 2 ) O(n^2) O(n2)的。
通过斜率优化(英文convex hull trick,凸壳优化),把时间复杂度优化到 O ( n ) O(n) O(n)。
斜率优化的核心技术是斜率(凸壳)模型和单调队列。
1. 把状态方程变换为平面的斜率问题
方程对某个固定的 i i i,求 j j j变化时 d p [ i ] dp[i] dp[i]的最优值,所以可以把关于 i i i的部分看成固定值,把关于 j j j的部分看成变量。把 m i n min min去掉,方程转化为:
d p [ j ] = a [ i ] ∗ d [ j ] + d p [ i ] dp[j] = a[i]*d[j] + dp[i] dp[j]=a[i]∗d[j]+dp[i]
为方便观察,令: y = d p [ j ] y = dp[j] y=dp[j], x = d [ j ] x = d[j] x=d[j], k = a [ i ] k = a[i] k=a[i], b = d p [ i ] b = dp[i] b=dp[i],方程变为:
y = k x + b y = kx + b y=kx+b
斜率优化的数学模型,就是把状态转移方程转换为平面坐标系直线的形式: y = k x + b y = kx + b y=kx+b。其中:
(1)变量 x x x、 y y y和 j j j有关,并且只有 y y y中包含 d p [ j ] dp[j] dp[j]。点 ( x , y ) (x, y) (x,y)是题目中可能的决策。
(2)斜率 k k k、截距 b b b与 i i i有关,并且只有 b b b中包含 d p [ i ] dp[i] dp[i]。最小的 b b b包含最小的 d p [ i ] dp[i] dp[i],也就是状态方程的解。
注意应用斜率优化的2个条件: x x x和 k k k是单调增加的,即 x x x随着 j j j递增而递增, k k k随着 i i i递增而递增。
2. 求一个dp[i]
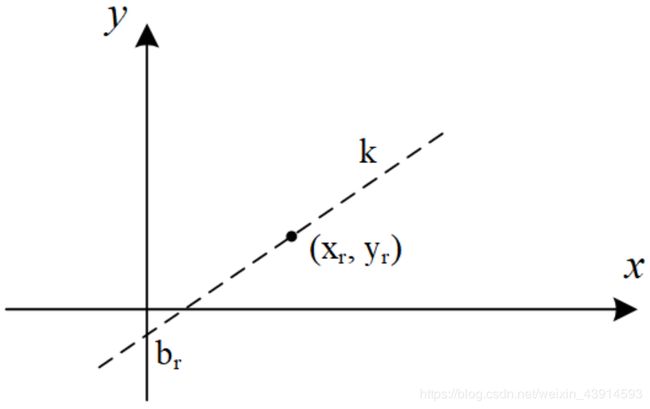
先考虑固定 i i i的情况下求 d p [ i ] dp[i] dp[i]。由于 i i i是定值,那么斜率 k = a [ i ] k = a[i] k=a[i]可以看成常数。当 j j j在 0 ≤ j < i 0≤j0≤j<i内变化时,对某个 j r j_r jr,产生一个点 v r = ( x r , y r ) v_r=(x_r, y_r) vr=(xr,yr),这个点在一条直线 y = k x + b r y = kx + b_r y=kx+br上, b r b_r br是截距。如图1。
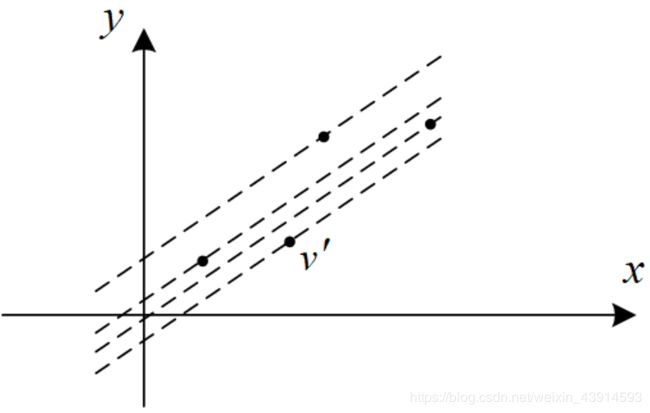
对于 0 ≤ j < i 0≤j0≤j<i中所有的 j j j,把它们对应的点都画在平面上,这些点对应的直线的斜率 k = a [ i ] k= a[i] k=a[i]都相同,只有截距 b b b不同。在所有这些点中,有一个点 v ′ v' v′所在的直线有最小截距 b ′ b' b′,算出 b ′ b' b′,由于 b ′ b' b′中包含 d p [ i ] dp[i] dp[i],那么就算出了最优的 d p [ i ] dp[i] dp[i]。如图2。
如何找最优点 v ′ v' v′?利用“下凸壳”。
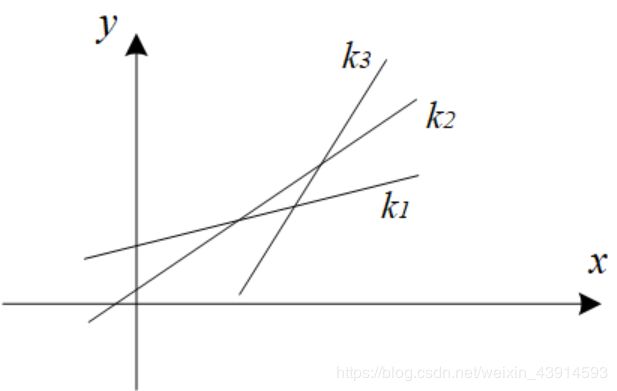
前面提到, x x x是单调增加的,即 x x x随着 j j j递增而递增。图3(1)中给出了了4个点,它们的 x x x坐标是递增的。
图3(1)中的1、2、3构成了“下凸壳”,“下凸壳”的特征是线段12的斜率小于线段23的斜率。2、3、4构成了“上凸壳”。经过上凸壳中间点3的直线,其截距b肯定小于经过2或4的有相同斜率的直线的截距,所以点3肯定不是最优点,去掉它。
去掉“上凸壳”后,得到图3(2),留下的点都满足“下凸壳”关系。最优点就在“下凸壳”上。例如在图3(3)中,用斜率为 k k k的直线来切这些点,设线段12的斜率小于 k k k,24的斜率大于 k k k,那么点2就是“下凸壳”的最优点。
以上操作用单调队列编程很方便。
(1)进队操作,在队列内维护一个“下凸壳”,即每2个连续点组成的直线,其斜率是单调上升的。新的点进队列时,确保它能与队列中的点一起仍然能够组成“下凸壳”。例如队列尾部的2个点是 v 1 v_1 v1、 v 2 v_2 v2,准备加入队列的新的点是 v 3 v_3 v3。比较 v 1 v_1 v1、 v 2 v_2 v2、 v 3 v_3 v3,看线段 v 1 v 2 v_1v_2 v1v2和 v 2 v 3 v_2v_3 v2v3的斜率是否递增,如果是,那么 v 1 v_1 v1、 v 2 v_2 v2、 v 3 v_3 v3形成了“下凸壳”;如果斜率不递增,说明 v 2 v_2 v2不对,从队尾弹走它;然后继续比较队列尾部的2个点和 v 3 v_3 v3;重复以上操作,直到 v 3 v_3 v3能进队为止。经过以上操作,队列内的点组成了一个大的“下凸壳”,每2个点组成的直线,斜率递增,队列保持为单调队列。
(2)出队列,找到最优点。设队头的2个点是 v 1 v_1 v1、 v 2 v_2 v2,如果线段 v 1 v 2 v_1v_2 v1v2的斜率比 k k k小,说明 v 1 v_1 v1不是最优点,弹走它,继续比较队头新的2个点,一直到斜率大于 k k k为止,此时队头的点就是最优点 v ′ v' v′。
3. 求所有的dp[i]
以上求得了一个 d p [ i ] dp[i] dp[i],复杂度 O ( n ) O(n) O(n)。如果对所有的 i i i,每一个都这样求 d p [ i ] dp[i] dp[i],总复杂度仍然是 O ( n 2 ) O(n^2) O(n2)的,并没有改变计算的复杂度。有优化的方法吗?
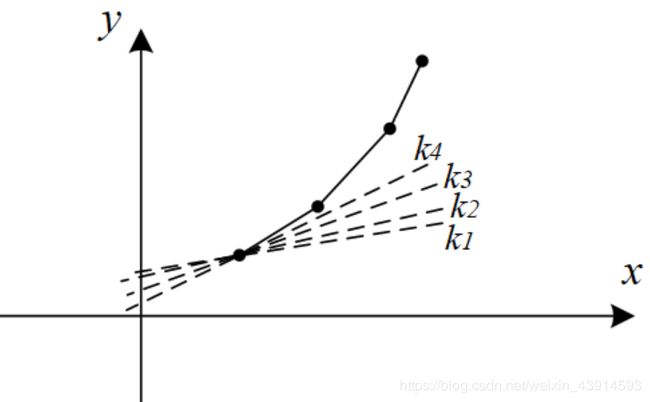
一个较小的 i 1 i_1 i1,它对应的点是{ v 0 , v 1 , . . . , v i 1 v_0, v_1, ..., v_{i1} v0,v1,...,vi1};一个较大的 i 2 i_2 i2,对应了更多的点{ v 0 , v 1 , . . . , v i 1 , . . . , v i 2 v_0, v_1, ..., v_{i1}, ..., v_{i2} v0,v1,...,vi1,...,vi2},其中包含了 i 1 i_1 i1的所有点。当寻找 i 1 i_1 i1的最优点时,需要检查{ v 0 , v 1 , . . . , v i 1 v_0, v_1, ..., v_{i1} v0,v1,...,vi1};寻找i2的最优点时,需要检查{ v 0 , v 1 , . . . , v i 1 , . . . , v i 2 v_0, v_1, ..., v_{i1}, ..., v_{i2} v0,v1,...,vi1,...,vi2}。这里做了重复的检查,并且这些重复是可以避免的。这就是能优化的地方,仍然用“下凸壳”进行优化。
(1)每一个 i i i所对应的斜率 k i = a [ i ] k_i = a[i] ki=a[i]是不同的,根据约束条件 a [ i ] ≤ a [ i + 1 ] a[i]≤ a[i+1] a[i]≤a[i+1],当 i i i增大时,斜率递增。
(2)前面已经提到,对一个 i 1 i_1 i1找它的最优点的时候,可以去掉一些点,即那些斜率比 k i 1 k_{i1} ki1小的点。这些被去掉的点,在后面更大的 i 2 i_2 i2时,由于斜率 k i 2 k_{i2} ki2也更大,肯定也要被去掉。
根据(1)和(2)的讨论,优化方法是:对所有的 i i i,统一用一个单调队列处理所有的点;被较小的 i 1 i_1 i1去掉的点,被单调队列弹走,后面更大的 i 2 i_2 i2不再处理它们。
因为每个点只进入一次单调队列,总复杂度 O ( n ) O(n) O(n)。
下面的代码演示了以上操作。
//q[]是单调队列,head指向队首,tail指向队尾,slope()计算2个点组成的直线的斜率
for(int i=1;i<=n;i++){
while(head<tail && slope(q[head],q[head+1])<k) //队头的2个点斜率小于k
head++; //不合格,从队头弹出
int j = q[head]; //队头是最优点
dp[i] = ...; //计算dp[i]
while(head<tail && slope(i,q[tail-1])<slope(q[tail-1],q[tail])) //进队操作
tail--; //弹走队尾不合格的点
q[++tail] = i; //新的点进队列
}
为加深对上述代码的理解,考虑一个特例:进入队列的点都符合“下凸壳”特征,且这些点组成的直线的斜率大于所有的斜率 k i k_i ki,那么结果是:队头不会被弹出,进队的点也不会被弹出,队头被重复使用 n n n次。
4. 例题
下面用一个例题给出典型代码。
HDU 3507 Print Article http://acm.hdu.edu.cn/showproblem.php?pid=3507
题目描述:打印一篇包含N个单词的文章,第i个单词的打印成本为Ci。在一行中打印k个单词的花费是 ,M是一个常数。如何安排文章,才能最小化费用?
输入:有很多测试用例。对于每个测试用例,第一行中都有两个数字N和M(0≤n≤500000,0≤M≤1000)。然后,在接下来的2到N + 1行中有N个数字。输入用EOF终止。
输出:一个数字,表示打印文章的最低费用。
样例输入:
5 5
5
9
5
7
5
样例输出:
230
题目的意思是:有 N N N个数和一个常数 M M M,把这 N N N个数分成若干部分,每一部分的计算值为这部分数的和的平方加上 M M M,总计算值为各部分计算值之和,求最小的总计算值。由于 N N N很大, O ( N 2 ) O(N^2) O(N2)的算法超时。
设 d p [ i ] dp[i] dp[i]表示输出前 i i i个单词的最小费用,DP转移方程:
d p [ i ] = m i n { d p [ j ] + ( s u m [ i ] − s u m [ j ] ) 2 + M } dp[i] = min\{dp[j] + (sum[i]-sum[j])2 + M\} dp[i]=min{dp[j]+(sum[i]−sum[j])2+M} 0 < j < i 0
其中 s u m [ i ] sum[i] sum[i]表示前 i i i个数字和。
下面把DP方程改写为 y = k x + b y = kx + b y=kx+b的形式。首先展开方程:
d p [ i ] = d p [ j ] + s u m [ i ] ∗ s u m [ i ] + s u m [ j ] ∗ s u m [ j ] − 2 ∗ s u m [ i ] ∗ s u m [ j ] + M dp[i] = dp[j] + sum[i]*sum[i] + sum[j]*sum[j] - 2*sum[i]*sum[j] + M dp[i]=dp[j]+sum[i]∗sum[i]+sum[j]∗sum[j]−2∗sum[i]∗sum[j]+M
移项得:
d p [ j ] + s u m [ j ] ∗ s u m [ j ] = 2 ∗ s u m [ i ] ∗ s u m [ j ] + d p [ i ] − s u m [ i ] ∗ s u m [ i ] − M dp[j] + sum[j]*sum[j] = 2*sum[i]*sum[j] + dp[i]-sum[i]*sum[i] - M dp[j]+sum[j]∗sum[j]=2∗sum[i]∗sum[j]+dp[i]−sum[i]∗sum[i]−M
对照 y = k x + b y = kx + b y=kx+b,有:
y = d p [ j ] + s u m [ j ] ∗ s u m [ j ] y = dp[j] + sum[j]*sum[j] y=dp[j]+sum[j]∗sum[j], y y y只和 j j j有关。
x = 2 ∗ s u m [ j ] x = 2*sum[j] x=2∗sum[j], x x x只和 j j j有关,且随着 j j j递增而递增。
k = s u m [ i ] k = sum[i] k=sum[i], k k k只和 j j j有关,且随着 i i i递增而递增。
b = d p [ i ] − s u m [ i ] ∗ s u m [ i ] − M b = dp[i] - sum[i]*sum[i] - M b=dp[i]−sum[i]∗sum[i]−M, b b b只和i有关,且包含 d p [ i ] dp[i] dp[i]。
下面给出代码。
#include 5. 习题
(1)洛谷P3195 玩具装箱 https://www.luogu.com.cn/problem/P3195
DP方程: d p [ i ] = m i n { d p [ j ] + ( s u m [ i ] + i − s u m [ j ] − j − L − 1 ) 2 } dp[i]=min\{dp[j]+(sum[i]+i−sum[j]−j−L−1)^2\} dp[i]=min{dp[j]+(sum[i]+i−sum[j]−j−L−1)2}
(2)洛谷4072 SDOI2016征途 https://www.luogu.com.cn/problem/P4072
二维斜率优化,DP方程: d p [ i ] [ p ] = m i n { d p [ j ] [ p − 1 ] + ( s [ i ] − s [ j ] ) 2 } dp[i][p]=min\{dp[j][p−1]+(s[i]−s[j])^2\} dp[i][p]=min{dp[j][p−1]+(s[i]−s[j])2}