中国大学MOOC-陈越、何钦铭-数据结构-2019夏期末考试（含答案）

中国大学MOOC-陈越、何钦铭-数据结构-2019夏期末考试（含答案）

判断题

1-1
  对N个不同的数据采用冒泡排序进行从大到小的排序，当元素基本有序时交换元素次数肯定最多。 (2分)
1-2
  NlogN^​2和NlogN具有相同的增长速度。 (2分)
1-3
  采用平方探测冲突解决策略（h_​i(k)=(H(k)+i​²)%11, 注意：不是±i^​2），将一批散列值均等于2的对象连续插入一个大小为11的散列表中，那么第4个对象一定位于下标为0的位置。 (2分)
1-4
  在一个有向图中，所有顶点的入度与出度之和等于所有边之和的2倍。 (2分)
1-5
  若一棵平衡二叉树的所有非叶结点的平衡因子都是0，则其必为完美二叉树。(2分)

Key：1-5 FTTTT

单选题

2-1
  在拓扑排序算法中用堆栈和用队列产生的结果会不同吗？(2分)
A. 有可能会不同
B. 以上全不对
C. 肯定是相同的
D. 是的肯定不同
2-2
  数据结构中Dijkstra算法用来解决哪个问题？ (2分)
A. 拓扑排序
B. 字符串匹配
C. 关键路径
D. 最短路径
2-3
  给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为： (2分)

A. V1,V3,V4,V5,V2
B. V1,V4,V3,V5,V2
C. V1,V2,V3,V5,V4
D. V1,V2,V4,V5,V3
2-4
  设一个栈的输入序列是1、2、3、4、5，则下列序列中，是栈的合法输出序列的是？ (4分)
A. 5 1 2 3 4
B. 4 3 1 2 5
C. 4 5 1 3 2
D. 3 2 1 5 4
2-5
  在并查集问题中，已知集合元素0~8所以对应的父结点编号值分别是{ 1, -4, 1, 1, -3, 4, 4, 8, -2 }（注：−n表示树根且对应集合大小为n），那么将元素6和8所在的集合合并（要求必须将小集合并到大集合）后，该集合对应的树根和父结点编号值分别是多少？ (4分)
A. 8和-5
B. 8和-6
C. 4和-5
D. 1和-6
2-6
  要判断一个整数N（>10）是否素数，我们需要检查3到√​N之间是否存在奇数可以整除N。则这个算法的时间复杂度是：(2分)
A. O(0.5logN)
B. O(√N)
​C. O(√​NlogN)
D. O(N/2)
​​2-7
  给定输入序列 {4371, 1323, 6173, 4199, 4344, 9679, 1989} 以及散列函数 h(X)=X%10。如果用大小为10的散列表，并且用分离链接法解决冲突，则输入各项经散列后在表中的下标为：（-1表示相应的插入无法成功）(4分)
A. 1, 3, 3, 9, 4, 9, 9
B. 1, 3, 4, 9, 5, 0, 8
C. 1, 3, 4, 9, 5, 0, 2
D. 1, 3, 4, 9, 7, 5, -1
2-8
  设最小堆（小根堆）的层序遍历结果为{5, 18, 15, 28, 22, 42, 40}。用线性时间复杂度的算法将该堆调整为最大堆（大根堆），则该树的中序遍历结果为：(4分)
A. 18, 28, 22, 15, 40, 5, 42
B. 22, 5, 18, 42, 40, 15, 28
C. 18, 28, 22, 42, 15, 40, 5
D. 5, 22, 18, 42, 15, 40, 28
2-9
  将1~6这6个键值插到一棵初始为空的二叉搜索树中。如果插入完成后，搜索树结构如图所示，问：可能的插入序列是什么？ (2分)

A. 4 1 2 3 5 6
B. 4 1 3 2 5 6
C. 1 2 3 4 5 6
D. 4 1 3 2 6 5
2-10
  将 8, 9, 7, 2, 3, 5, 6, 4 顺序插入一棵初始为空的AVL树。下列句子中哪句是错的？ (4分)
A. 3 和 8 是兄弟
B. 7 是根结点
C. 4 和 6 是兄弟
D. 5 是 8 的父结点
2-11
  在图中自a点开始进行广度优先遍历算法可能得到的结果为： (2分)

A. a, e, b, c, f, d
B. a, b, e, c, d, f
C. a, e, d, f, c, b
D. a, c, f, e, b, d
2-12
将序列{ 2, 12, 16, 88, 5, 10, 34 }排序。若前2趟排序的结果如下：
  第1趟排序后：2, 12, 16, 10, 5, 34, 88
  第2趟排序后：2, 5, 10, 12, 16, 34, 88
则可能的排序算法是：(2分)
A. 冒泡排序
B. 归并排序
C. 插入排序
D. 快速排序
2-13
  对给定序列{ 110，119，7，911，114，120，122 }采用次位优先（LSD）的基数排序，则两趟收集后的结果为： (2分)
A. 110, 120, 911, 122, 114, 7, 119
B. 7, 110, 119, 114, 911, 122, 120
C. 7, 110, 911, 114, 119, 120, 122
D. 7, 110, 119, 114, 911, 120, 122
2-14
  将10、12、1、14、6、5、8、15、3、9、7逐个按顺序插入到初始为空的最小堆（小根堆）中，然后连续执行两次删除最小元素操作（DeleteMin），此后堆顶的元素是什么？ (4分)
A. 5
B. 9
C. 7
D. 6
2-15
  设栈S和队列Q的初始状态均为空，元素a、b、c、d、e、f、g依次进入栈S。若每个元素出栈后立即进入队列Q，且7个元素出队的顺序是b、d、c、f、e、a、g，则栈S的容量至少是： (2分)
A. 1
B. 4
C. 2
D. 3
2-16
  下列叙述错误的是（）。 (2分)
A. 当一棵具有n 个叶子结点的二叉树的WPL 值为最小时，称其树为哈夫曼树，其二叉树的形状是唯一的
B. 哈夫曼树的结点个数不能是偶数
​C. 哈夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近
D. 一棵哈夫曼树的带权路径长度等于其中所有分支结点的权值之和
​​2-17
  已知一棵二叉树的树形如下图所示，其后序序列为{ e, a, c, b, d, g, f}。树中与结点a同层的结点是：(2分)

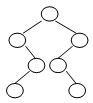
A. c
B. f
C. g
D. d
2-18
  给定有权无向图的邻接矩阵如下，其最小生成树的总权重是： (4分)

A. 12
B. 14
C. 11
D. 10
2-19
  给定散列表大小为17，散列函数为H(Key)=Key%17。采用平方探测法处理冲突：h_​i(k)=(H(k)±i​²)%17将关键字序列{ 23, 22, 7, 26, 9, 6 }依次插入到散列表中。那么元素6存放在散列表中的位置是：(4分)
A. 15
B. 10
C. 2
D. 6
2-20
  在一个链队列中，front和rear分别为头指针和尾指针，则插入一个结点s的操作为（ ）。 (2分)
A. front=front->next;
B. s->next=front;front=s;
C. rear->next=s;rear=s;
D. s->next=rear;rear=s;
2-21
  对于序列{ 49，38，65，97，76，13，27，50 }，按由小到大进行排序，下面哪一个是初始步长为4的希尔排序法第一趟的结果？ (4分)
A. 49,13,27,50,76,38,65,97
B. 13,27,38,49,50,65,76,97
C. 49,76,65,13,27,50,97,38
D. 97,76,65,50,49,38,27,13
2-22
  在一个有权无向图中，如果顶点b到顶点a的最短路径长度是10，顶点c与顶点b之间存在一条长度为3的边。那么下列说法中有几句是正确的？ (4分)
1. c与a的最短路径长度就是13
2. c与a的最短路径长度就是7
3. c与a的最短路径长度不超过13
4. c与a的最短路径不小于7
A. 3句
B. 1句
C. 4句
D. 2句

Key：1-5 ADADC 6-10 BACBD 11-15 BDCAD 16-20 ADDCC 21-22 AD

程序填空题

5-1
  本函数的功能是从有N个元素的线性表A中查找第K大的元素。其中函数BuildMinHeap(H, K)是将元素H[1]… H[K]调整为一个最小堆。请完成下列填空。

ElementType FindKthLargest ( int A[], int N, int K )
{   /* it is assumed that K<=N */
    ElementType *H;
    int i, next, child;

    H = (ElementType *)malloc((K+1)*sizeof(ElementType));
    for ( i=1; i<=K; i++ ) H[i] = A[i-1];
    BuildMinHeap(H, K);

    for ( next=K; next<N; next++ ) {
        H[0] = A[next];
        if ( H[0] > H[1] ) {
            for ( i=1; i*2<=K; i=child ) {
                child = i*2;
                if ( child!=K && H[child+1]>H[child]/*(4分)*/ ) child++;
                if ( H[child]>H[0]/*(5分)*/ )
                    H[i] = H[child];
                else break;
            }
            H[i] = H[0];
        }
    }
    return H[1];
}

5-2
  下列代码的功能是利用散列函数hash将一个元素插入到散列表ht[]中。其中list类型的结点包含element类型的项item、以及一个next指针。如果插入成功，则函数返回1，否则返回0。

int insert( struct element item, list_pointer ht[] )
{
   int ret, hash_value;
   list_pointer ptr, trail, lead;

   ret = 1;
   hash_value = hash(item.key);
   trail = NULL; lead = ht[hash_value];
   for ( ; lead; trail = lead, lead = lead->next) {
      if (!strcmp(lead->item.key, item.key)) {
         printf("The key is in the table\n");
         ret = 0;
      }
   }
   if (ret) {
      ptr = (list_pointer)malloc(sizeof(struct list));
      ptr->item = item/*(3分)*/;
      ptr->next = NULL;
      if (trail)
         trail->next = ptr/*(3分)*/;
      else
         ht[hash_value] = ptr/*(3分)*/;
   }
   return ret;
}

编程题

7-1 根据后序和中序遍历输出先序遍历 (8 分)
本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果，输出该树的先序遍历结果。

输入格式:
第一行给出正整数N(≤30)，是树中结点的个数。随后两行，每行给出N个整数，分别对应后序遍历和中序遍历结果，数字间以空格分隔。题目保证输入正确对应一棵二叉树。

输出格式:
在一行中输出Preorder:以及该树的先序遍历结果。数字间有1个空格，行末不得有多余空格。

输入样例:

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例:

Preorder: 4 1 3 2 6 5 7

C语言实现：

#include
#include
struct BiTNode{
	struct BiTNode *lchild;
	struct BiTNode *rchild;
	int data;
};
typedef struct BiTNode *BiTree;
 
BiTree CreateTree(int *p, int *q, int n){
	if(n){
		BiTree T = (BiTree)malloc(sizeof(struct BiTNode));
		T->data = q[n-1];
		int i;
		for(i = 0; i < n; i++){
			if(q[n - 1] == p[i])
				break;
		}
		T->lchild = CreateTree(p, q, i);
		T->rchild = CreateTree(p + i + 1, q + i, n - i - 1);
		return T;
	}
    return NULL;
}
void PreorderTraversal(BiTree BT){
	if(BT){
        printf(" %d",BT->data);
		PreorderTraversal(BT->lchild);
		PreorderTraversal(BT->rchild);
	}
}
int main(){
	int n,i; 
	scanf("%d",&n);
	int p[30],q[30];
	BiTree T;
	for(i = 0; i < n; i++){
	    scanf("%d",&q[i]);
	}	
	for(i = 0; i < n; i++){
	 	scanf("%d",&p[i]);
	}
	T = CreateTree(p, q, n);
	printf("Preorder:");
	PreorderTraversal(T);
	return 0;
}