零基础学习AVL树的构造(附Java代码)
注:本文针对零基础选手,因此尽量不出现专有名词,如根节点、平衡因子等,并且忽略了一些细枝末节,例如:单个结点实际上也是一棵特殊的树。
打开这篇博客,我们很自然地会产生三个疑问:
1、什么是AVL树?
2、为什么要学习AVL树?
3、怎么使用AVL树?
本篇文章正是围绕解决这三个问题而展开的。
1、什么是AVL树?
首先我们先抛出一个问题作为引子:
现在随机的给出7个数字:
55、22、99、10、45、65、173。
我们要在这7个数字中,判断173是否在这7个数字当中,怎么办呢?计算机可不会像人们那样一眼就能看出来173在最后一个,计算机只能进行一个一个的比较。
于是,很直观的一个想法:将173与这7个数字进行从头到尾的比较。
| 比较数字 | 55 | 22 | 99 | 10 | 45 | 65 | 173 |
|---|---|---|---|---|---|---|---|
| 是否与173相等 | 不相等 | 不相等 | 不相等 | 不相等 | 不相等 | 不相等 | 相等 |
| 是否继续比较 | 继续比较 | 继续比较 | 继续比较 | 继续比较 | 继续比较 | 继续比较 | 停止比较 |
| 比较次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
我们可以从表格中看到,如果在7个数中查找某一个数字,那么当要查找的数字是这7个数中的最后一个时,需要的比较次数是7次。同理,如果要在1000个数中查找某一个数字,那么当要查找的数字是这1000个数中的最后一个时,最多要比较1000次!
比较次数如此之多,大大降低了查找效率,于是机智的人们就想到了换一种查找方式。
首先先把这7个数中的第一个数55存起来。
然后去处理这7个数中的第二个数22,发现它比55要小,于是把22放在55的下一层的左边。
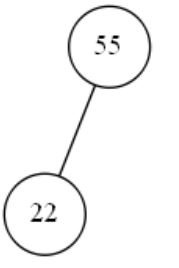
接下来处理这7个数中的第三个数99,发现它比55大,于是把99放在55的下一层的右边。
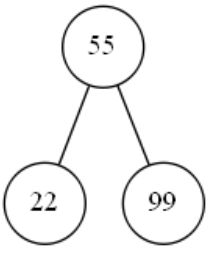
下一个待处理的是,第四个数字10,10比55小,但55的下一层的左边已经有数字22了,于是10应该放在22的下一层,10由于比22小,所以10放在22的下一层的左边。
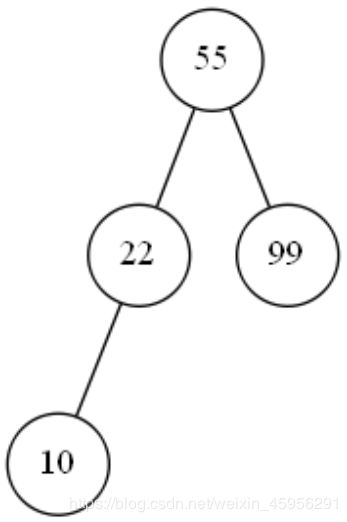
对于第五个数字45,45比55小,但55的下一层的左边已经有数字22了,于是45应该放在22的下一层,45比22大,所以45放在22的下一层的右边。
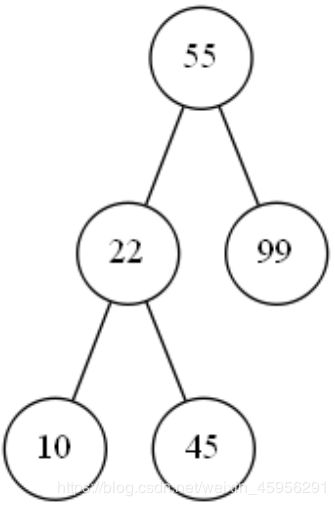
对于第六个数字65,65比55大,但55的下一层的右边已经有数字99了,于是65应该放在99的下一层,65由于比99小,所以65放在99的下一层的左边。
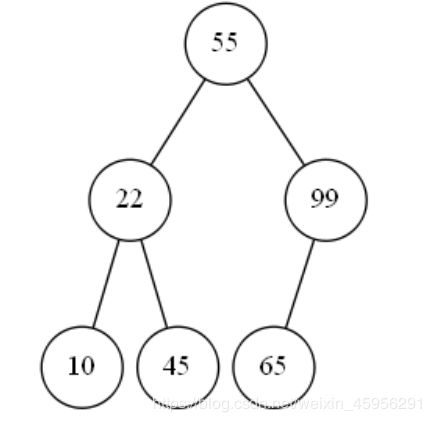
对于第七个数字173,173比55大,但55的下一层的右边已经有数字99了,于是173应该放在99的下一层,173由于比99大,所以173放在99的下一层的右边。
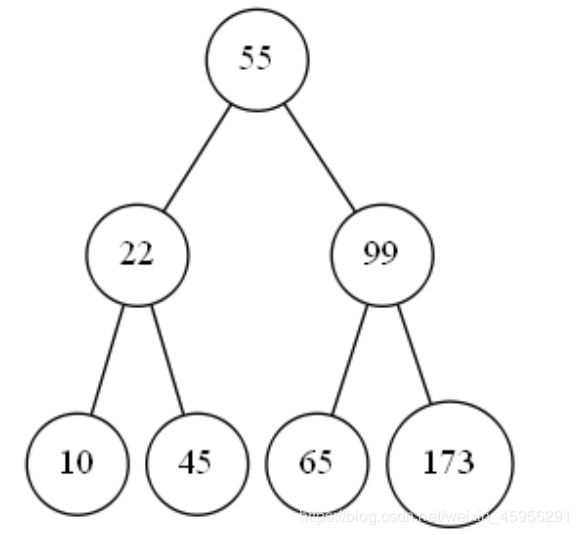
经过这样对七个数字的处理,我们再进行一次查找,同样的,查找七个数字中的最后一个数字173。
我们首先从最上一层数字55出发,比较173和55的大小;由于173比55大,所以173与55的下一层的右边数字99继续比较;由于173比99大,所以173与99的下一层的右边数字173继续比较;由于173等于173,于是结束比较,我们可以知道173在这7个数中。用这种比较方式,我们只比较3次就得到了答案,相比最初的从头到尾比较方式,这种方式的比较次数要少。
如果对于1000个数据,我们最多要比较多少次呢?
请看下图:
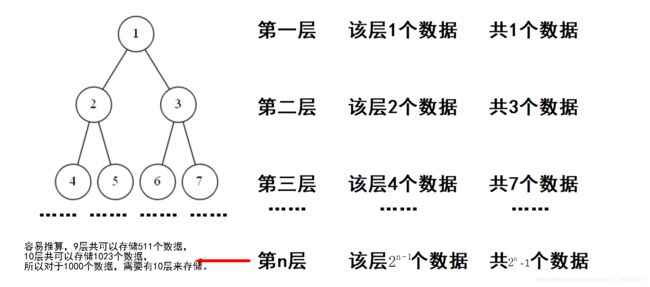
由图中可知,1000个数据需要有10层来存储,那么我们只要从第一层开始,一层一层的往下比较,最多只要比较10次就可以得到某个数是否在这1000个数中的答案了。
比较10次明显比比较1000次的效率要高,有没有感觉第二种方法更好?

在第二种比较方式中,我们用到了如下图所示的结构,这种结构就称为二叉树。
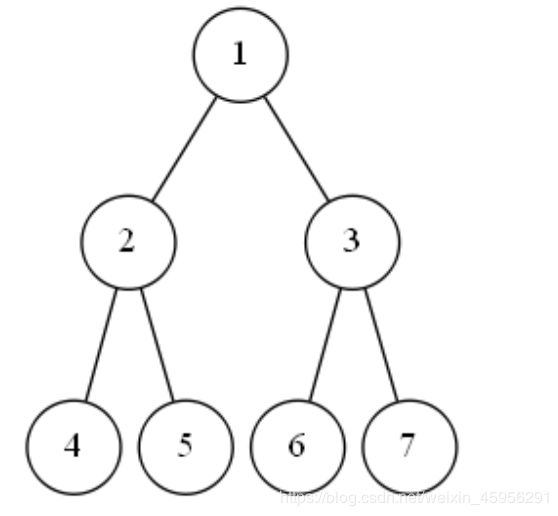
有些读者可能还是不明白什么是二叉树,没关系,请继续往下看。
二叉树,顾名思义,就是二叉的树。
抛开“二叉”先不管,什么是计算机领域中的树呢?
像这样:
我们先看一下在这些图中有什么特征,它们都有一个个小圆圈。
我们给这些圆圈起一个名字,叫做结点。
对于那些底下没有连接其他结点的结点,它还有一个别名,叫做叶子结点,简称叶子。
叶子结点所在的高度这里定义为1(要考试的同学请注意,有些教材把叶子结点高度定义为0,具体的叶子高度以你们老师所教的为准,只是一个规定而已)。
一个结点的高度等于该结点底下 “左边结点高度和右边结点高度的最大值” 加1。
提问:对于一个不存在的结点,如果非要求它的高度,那么答案是多少呢?
答案:对于一个不存在的结点,它的高度是0(可以理解成:规定一个不存在的结点,它的高度是0)。
上面出现的三个加粗的名词请大家记住,因为在下文中还会出现:结点、叶子结点、高度。

如果由一个结点往下延伸,构成了一棵像生活中倒挂树的结构,那么我们把这样的结构称为树。
生活中的一棵倒挂的树:

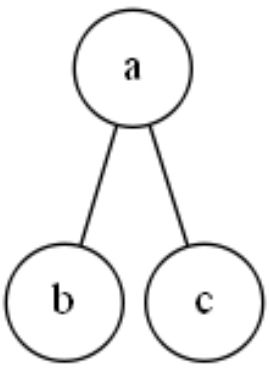
对于每一个结点下面,与该结点直接相连的其他结点,如果最多有两个,那么我们就称这样的树为二叉树。
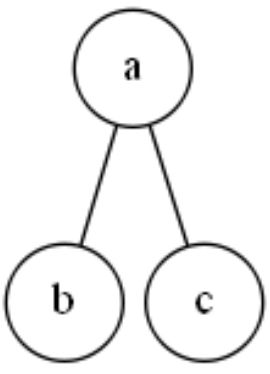
这就是一棵二叉树。
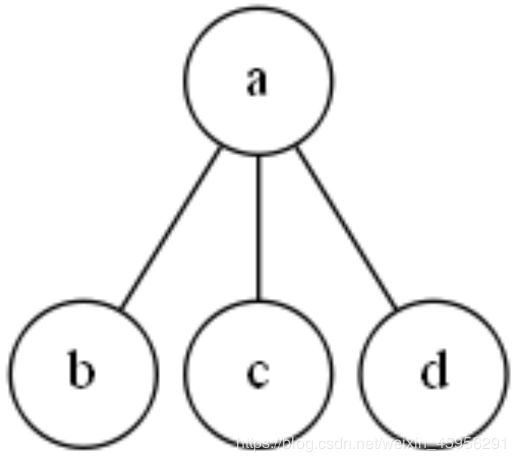
对于每一个结点下面,与该结点直接相连的其他结点,如果最多有三个,那么我们就称这样的树为三叉树。
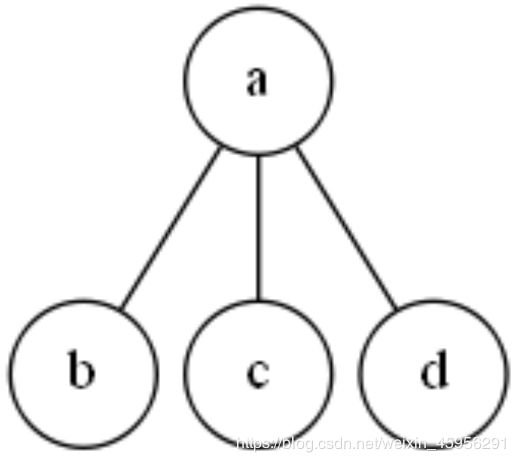
这就是一棵三叉树。
同样的,也有四叉树、五叉树……n叉树。
需要注意的是,我们这边说的都是“最多”,也就是对于一个n叉树而言,它的每一个结点下面,与该结点直接相连的其他结点个数,可以不是n个,只要保证与该结点直接相连的其他结点个数不超过n个即可。因此,二叉树一定是一个三叉树。
还要提到的一个重点是:实际上,在一棵二叉树中,对于任意一个结点,如果值比当前结点小的其他结点在当前结点左边,值比当前结点大的其他结点在当前结点右边,那么满足这两个条件的二叉树,我们称为二叉排序树。
下图就是一棵二叉排序树:
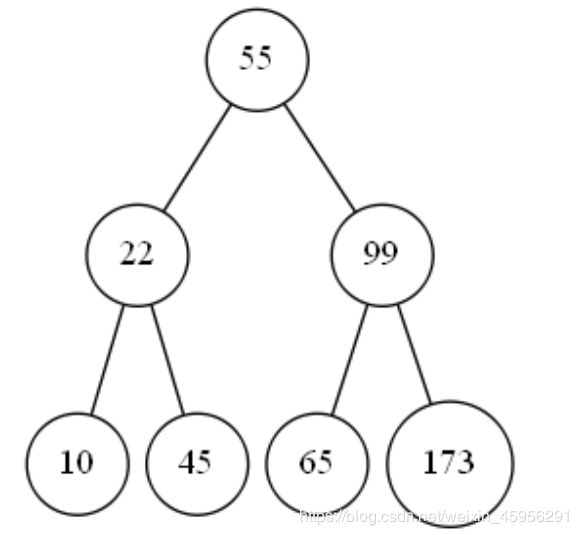
刚刚拿的是55、22、99、10、45、65、173这七个随机数字构造二叉排序树。

这次我不随机了,我给出1、2、3、4、5、6、7这七个数字,去判断7是否在这七个数字当中。
按照第一种方法,我们就从头到尾,一个个比较,很明显,要比较7次。
那如果使用第二种方法呢,用二叉排序树来进行比较,会不会减少比较次数呢?
下图,我给出了将1、2、3、4、5、6、7这七个数字直接构造二叉排序树后的构造结果。
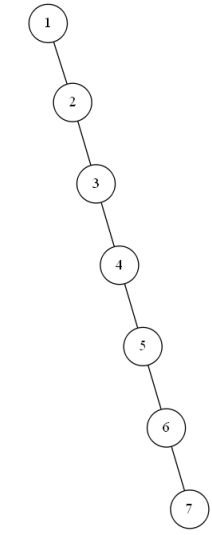
细心的小伙伴一定发现了,直接按照第二种方法构造的二叉排序树,在这新的七个数据下,新二叉排序树长得和之前不一样,这七个数据连成了一条线。
重要的是,如果我们要查找7这个数字到底在不在这里面,我们一样要比较7次,对于1000个数据,我们要比较1000次!

为了解决这个问题,我们要在第二个方法上加一些条件,使其不再变得像一条直线,而是尽量“分散开”。
“分散开”是什么意思?
我们知道,对于1000个数据,如果构成的二叉排序树有1000层,那么最多要比较1000次;如果构成的二叉排序树只有10层,那么最多只要比较10次。
对于7个数据,如果构成的二叉排序树有7层,那么最多要比较7次;如果构成的二叉排序树只有3层,那么最多只要比较3次。
所以,“分散开”的意思就是尽量使构成的二叉排序树的层数少。
那怎样去构造二叉排序树才能使二叉排序树的层数尽量少呢?
答案是:在构造二叉排序树时,边构造边检查。当某一个结点底下连着的左结点高度比右结点高度大1,或者某一个结点底下连着的右结点高度比左结点高度大1时,我们就对该结点进行调整,使其底下左结点和右结点的高度差的绝对值不大于1,换句话说,要使高度差的绝对值为0或1。
而之前的第二种方法,缺陷就在于没考虑到这一点,之前的第二种方法,只是简单地把比当前结点值小的结点放在当前结点下一层的左边,把比当前结点值大的结点放在当前结点下一层的右边。
至此,我们可以回答本篇文章开头提到的第一个问题了。什么是AVL树?AVL树又名平衡二叉排序树,顾名思义,AVL树是一个平衡的、二叉的、排序的树。
树的概念我们来回顾一下:如果由一个结点往下延伸,构成了一棵像生活中倒挂树的结构,那么我们把这样的结构称为树。
再来回顾一下二叉的概念:对于每一个结点下面,与该结点直接相连的其他结点,如果最多有两个,那么就称这样的树为二叉树。
然后回顾一下二叉排序树的概念:在一棵二叉树中,对于任意一个结点,如果值比当前结点小的其他结点在当前结点左边,值比当前结点大的其他结点在当前结点右边,那么满足这两个条件的二叉树,我们称为二叉排序树。
接下来回顾一下平衡的概念:对于某一个结点,它底下左结点和右结点的高度差值的绝对值如果不大于1,则称这个结点是平衡的。
最后总结一下平衡二叉排序树的概念:在一棵二叉排序树中,对每一个结点而言,它底下的左结点和右结点的高度差值的绝对值不大于1,则称这样的二叉排序树为平衡二叉排序树,即AVL树(拓展:AVL树得名于发明它的人G. M. Adelson-Velsky和E. M. Landis),平衡二叉排序树又称平衡二叉搜索树、平衡二叉查找树,简称平衡二叉树。
2、为什么要学习AVL树?
经过第一部分的学习,相信你已经能很容易的回答出第二个问题了。为什么要学习AVL树?答案是:为了使查找效率大大提高,在1000个数据中进行查找时,能只查找10次而不是1000次,在100000000个数据中进行查找时,能只查找27次而不是100000000次。
能只查找27次的计算方法是:根据 2 n − 1 ≥ 100000000 , 2^n - 1 ≥ 100000000, 2n−1≥100000000, 算出一个n的最小值。这个公式在这张图片中有体现(即使不会计算也不影响继续往下学习)。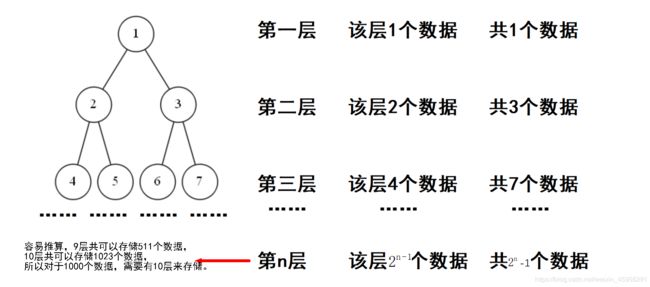
3、怎么使用AVL树?
要使用AVL树,就得先构造一个AVL树。
由第一部分可以知道,构造AVL树其实就是在构造二叉排序树的基础上增加了调整规则,使得对二叉排序树中的任意一个结点而言,它底下的左结点和右结点的高度差的绝对值不大于1。
问题来了,需要调整的情况具体有哪些?怎么进行调整?

需要调整的情况有四种:
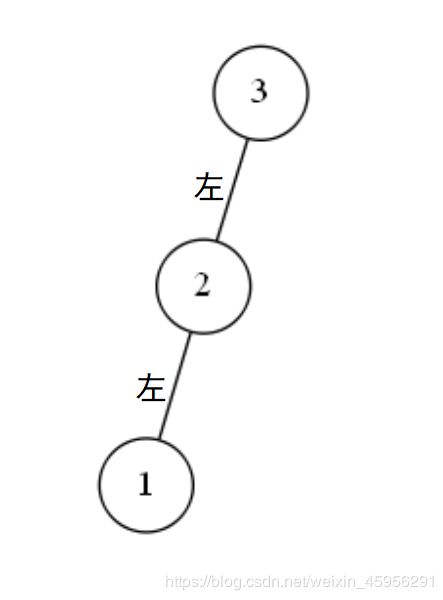
第一种情况:
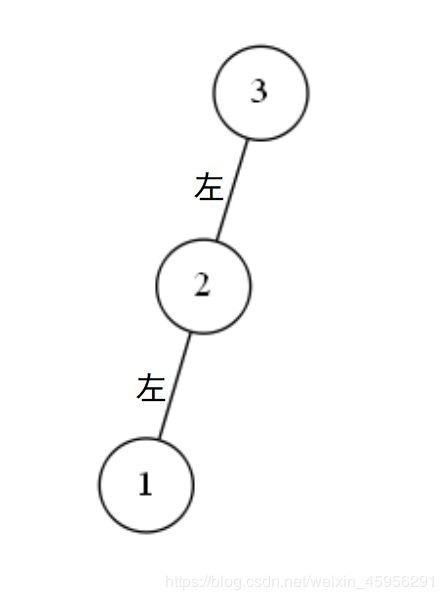
值为3的结点,它底下的左结点的高度为2,而底下右结点的高度为0;值为1的结点是不平衡点。
(
在第一部分里,我们提到过,对于一个不存在的结点,它的高度是0。
如图:

)
像图中这种样子的不平衡情况,我们称为左左情况。
第二种情况:
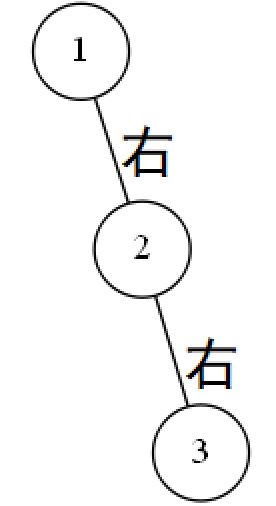
值为1的结点,它底下的左结点的高度为0,而底下右结点的高度为2;值为1的结点是不平衡点。
像图中这种样子的不平衡情况,我们称为右右情况。
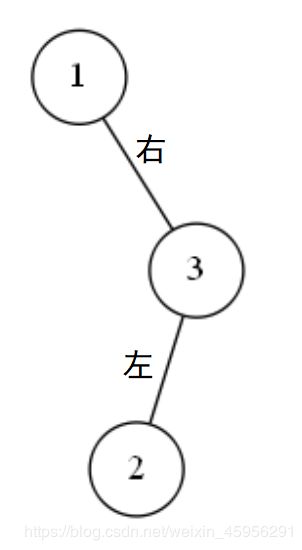
第三种情况:
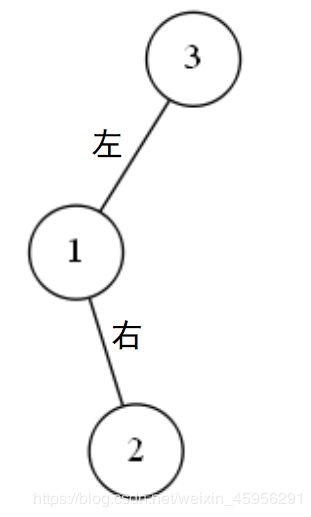
值为3的结点,它底下的左结点的高度为2,而底下右结点的高度为0;值为3的结点是不平衡点。
像图中这种样子的不平衡情况,我们称为左右情况。
第四种情况:
值为1的结点,它底下的左结点的高度为0,而底下右结点的高度为2;值为1的结点是不平衡点。
像图中这种样子的不平衡情况,我们称为右左情况。
这就是所有需要进行调整的情况。有小伙伴可能会问了,会不会出现像“右右右情况”呢?
我们来画个图就知道了。
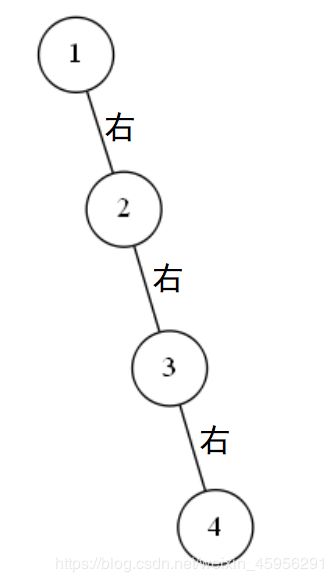
我们最后处理的数字一定是4,但是,实际上我们在处理数字3时,数字1所在的结点就已经出现不平衡的情况了,而且不平衡情况为“右右情况”,这时候就已经要对数字1所在结点进行调整,所以不会出现“右右右情况”。
说完了四种不平衡的情况:左左情况、右右情况、左右情况、右左情况。接下来的最后一个问题便是:该如何进行调整?
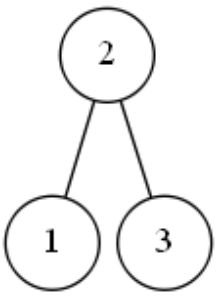
对于左左情况,我们的调整策略是:把2结点往上提,把3所在的结点作为2结点的下一层的右边结点。
请看图:
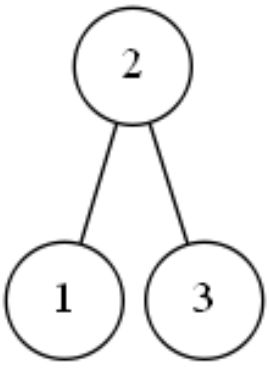
经过这样的调整,原本连成一条线的数字3、2、1就很好的“分散开”了,我们成功地把3层的二叉排序树变为了2层。
2、右右情况:
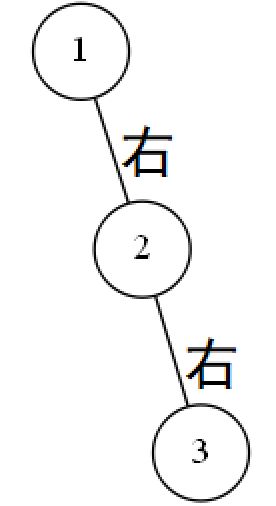
类似“左左情况”,右右情况的调整策略是:把2结点往上提,把1所在的结点作为2结点的下一层的左边结点。
请看图:
再来看看剩下的两种情况。
3、左右情况:
![]()
左右情况里面包含了两个方向:“左”和“右”,所以我们的调整也包含两步。
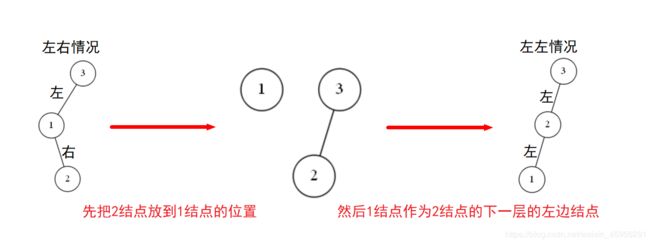
第一步:
先把2结点放到1结点的位置,然后1结点作为2结点的下一层的左边结点,使“左右情况”变成“左左情况”。
请看图:
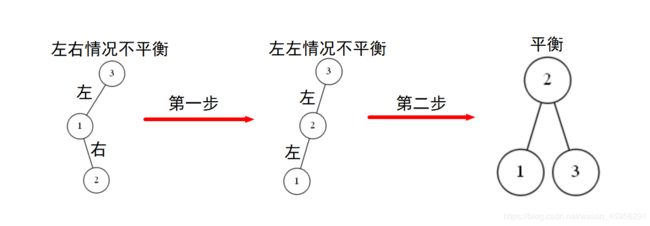
第二步:
一旦变成了“左左情况”,也就回到情况一,那么再进行一步调整,就能使结点“分散开”了。
情况一的调整策略上面已经给出,下图是两步调整过程。
4、右左情况:
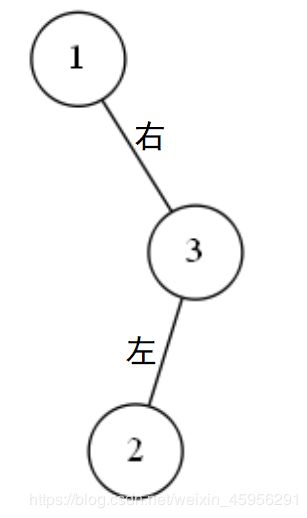
类似左右情况:右左情况里面包含了两个方向:“右”和“左”,所以我们的调整也包含两步。
第一步:
先把2结点放到3结点的位置,然后3结点作为2结点的下一层的右边结点,使“右左情况”变成“右右情况”。
请看图:
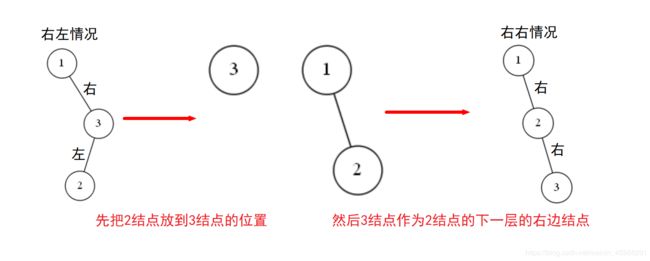
第二步:
一旦变成了右右情况”,也就回到情况二,那么再进行一步调整,就能使结点“分散开”了。
情况二的调整策略上面已经给出,下图是两步调整过程。
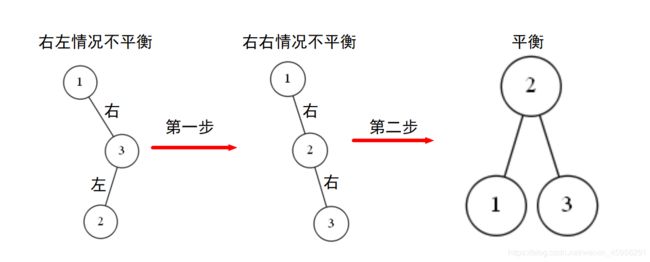
至此,我们已经学会了当二叉排序树中结点不平衡时,对不平衡结点进行调整的方法。
还记得之前对1、2、3、4、5、6、7这七个数进行构造二叉树时,这七个数连成了一条线的情形吗?接下来,我们还是用这七个数,但是这次就不是简单的构造二叉排序树了,我们要构造一个平衡二叉排序树,即AVL树。构造AVL树后,我们再来看看,查找这7个数中的任意一个数,最多要查找几次。
对1、2、3、4、5、6、7这七个数构造AVL树。
首先把1这个数存起来。

再处理2这个数,2比1大,所以2放在1的下一层的右边。

接下来处理3这个数,3比1大,所以3应该放在1的下一层的右边,但是1的下一层的右边已经有2了,所以3放在2的下一层;3比2大,所以3放在2的下一层了的右边。
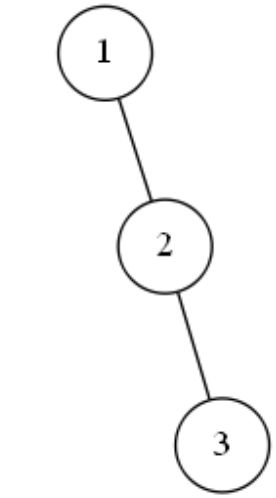
细心的小伙伴发现了,当处理完3后,1不平衡了:1的下一层的左边结点的高度为0,1的下一层的右边结点的高度为2,0和2差值的绝对值是2,2大于1,所以对1这个结点来说,是不平衡的。

要进行调整!
这是右右情况的不平衡,根据右右情况的调整策略:把2结点往上提,把1所在的结点作为2结点的下一层的左边结点。
调整后的结果如图:

经过调整,现在这三个结点都达到了平衡状态。我们可以继续对后面的数据进行处理。
下一个数字是4,4比2大,所以应该放在2的下一层的右边,但是2的下一层的右边已经有数字3了,所以4应该放在3的下一层;4比3大,所以4要放在3的下一层的右边。
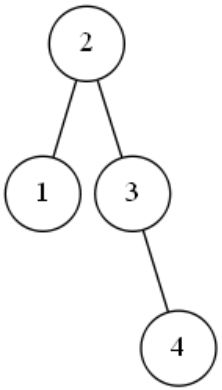
这时,没有一个结点是不平衡的,所有结点底下左结点和右结点的高度差的绝对值为0或1。不用调整。
再处理数字5。5比2大,所以应该放在2的下一层的右边,但是2的下一层的右边已经有数字3了,所以5应该放在3的下一层;5比3大,所以5要放在3的下一层的右边,但是3的下一层的右边已经有数字4了,所以5应该放在4的下一层;5比4大,所以5应该放在4的下一层的右边。
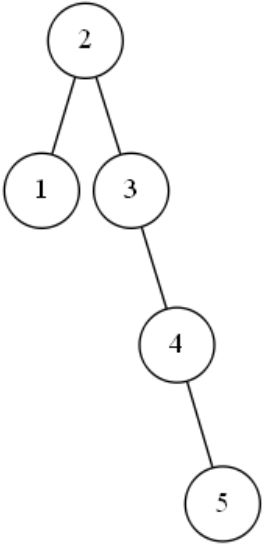
我们发现这时候,3结点是不平衡的,要进行调整,这种不平衡还是一个右右情况,根据右右情况的调整策略,我们要把4结点往上提,把3所在的结点作为4结点的下一层的左边结点。
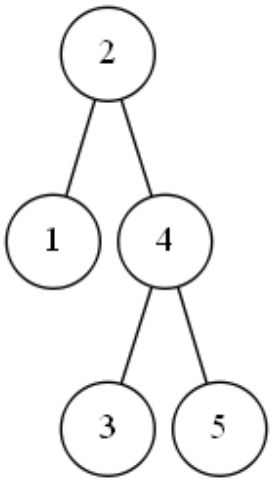
这时,没有一个结点是不平衡的,所有结点底下左结点和右结点的高度差的绝对值为0或1。不用调整。
继续处理数字6。6比2大,所以6应该放在2的下一层的右边,但是2的下一层的右边已经有数字4了,所以6应该放在4的下一层;6比4大,所以6要放在4的下一层的右边,但是4的下一层的右边已经有数字5了,所以6应该放在5的下一层;6比5大,所以6应该放在5的下一层的右边。
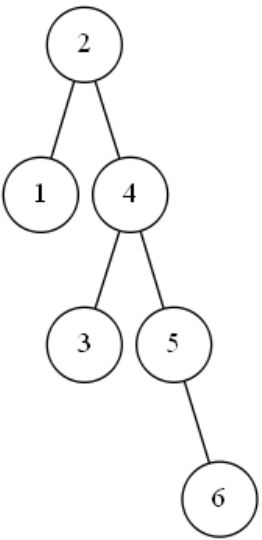
这时候有没有一个结点不平衡呢?有,2结点不平衡了。2结点底下左边1结点的高度为1,2结点底下右边4结点的高度为3,1和3的差值的绝对值为2,大于1了,所以2结点不平衡。那么具体是四种不平衡情况的哪一种呢?
由于2结点底下右边结点的高度比左边结点的高度要大,所以一定是“右*情况”;那么是右左情况还是右右情况呢?
由于6结点的上一个结点数字是5,而6比5大,所以6在5的底下的右边,因此是右右情况。
进行调整。
这种右右情况和之前的右右情况不太一样,区别在于:我们除了有要调整的2、4、5这三个结点外,还多了1、3、6这三个结点。不过没关系,我们先不看1、3、6这三个结点,先调整2、4、5三个结点。
2、4、5的调整结果:
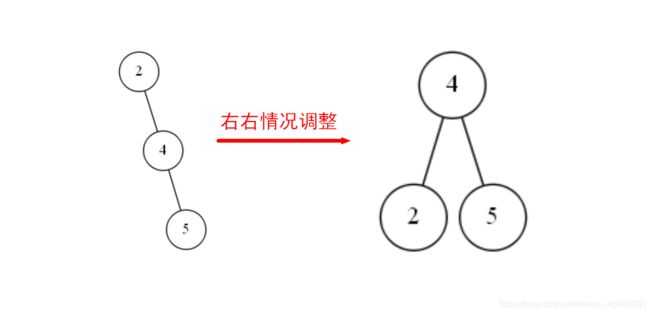
接下来考虑1、3、6这三个结点的放置位置。
1结点原本在2结点底下的左边,调整后继续放回原位置。
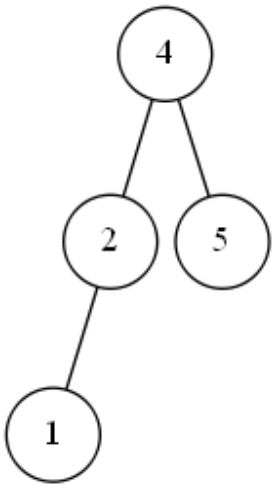
3结点原本在4结点底下的左边,调整后本应该继续放回原位置,但是调整后,4结点底下的左边已经有一个结点2了,于是3就放在2结点的底下的右边(这是调整方法)。
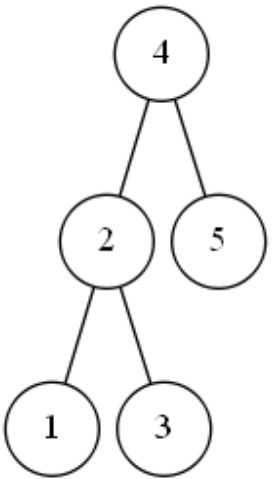
6结点原本在5结点底下的右边,调整后继续放回原位置。
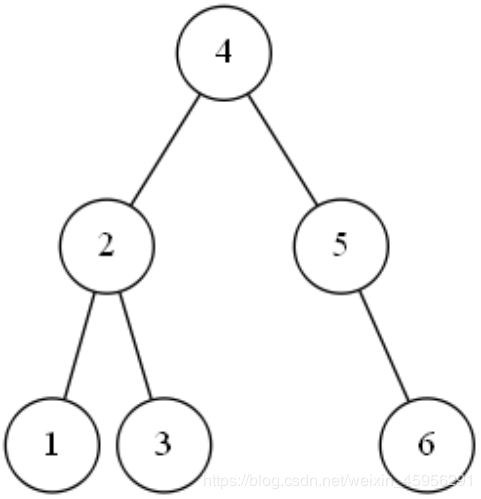
最后处理第七个数字7,7比4大,所以7应该放在4的下一层的右边,但是4的下一层的右边已经有5了,所以7放在5的下一层;7比5大,所以7放在5的下一层的右边,但是5的下一层的右边已经有6了,所以7放在6的下一层;7比6大,所以7放在6的下一层的右边。
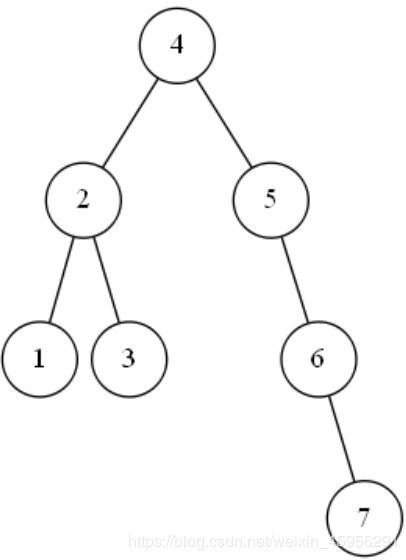
我们发现,5结点是不平衡的,要进行调整,这种不平衡是一个右右情况,根据右右情况的调整策略,我们要把6点往上提,把5所在的结点作为6结点的下一层的左边结点。
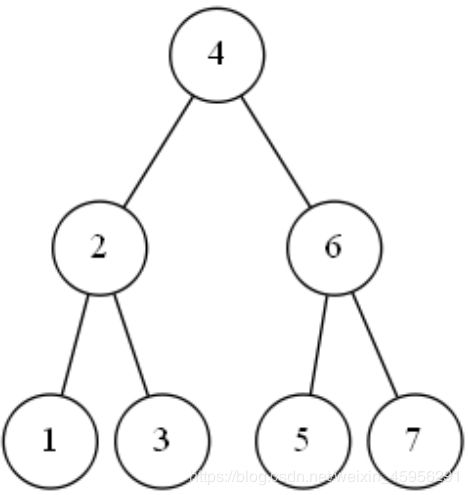
完成了AVL树的构造,我们接下来再尝试查找一个数据,查找最后一个数字7。首先7与最上面一个结点4比较,7比4大,于是7和结点4下面一层的右边结点6进行比较;7比6大,于是7和结点6下面一层的右边结点7进行比较,;7和7相等,于是结束比较。整个比较次数是3次。
至此,我们完成了AVL树的构造,并懂得如何使用AVL树进行查找。

感谢阅读,欢迎交流!
以下是Java实现的代码,虽然代码基本上逐行注释,但是代码部分仍然不适合完全零基础选手。
//本代码实现:从文件中读取数据,并根据AVL树构建规则,构建AVL树,然后从控制台输出平均查找长度ASL。
import java.io.File;//用于文件读写
import java.io.FileNotFoundException;//用于找不到文件时异常处理
import java.util.Scanner;//用于控制台输出
public class AVLTree {//AVLtree类
private static class Node{//Node类
int h;//树的高度
int element;//数据域
Node left;//左子树
Node right;//右子树
Node parent;//父结点
//Node类的构造方法
public Node(int element, int h, Node left, Node right, Node parent){
this.element = element;//设置数据值
this.h = h;//设置当前结点的高度
this.left = left;//设置左孩子
this.right = right;//设置右孩子
this.parent = parent;//设置父结点
}
}
private Node root;//指向当前子树根节点的引用,不是整棵树的根
private int size = 0;//节点个数,设置初始值为0
//AVLtree类的构造函数
public AVLTree(){
root = new Node(0, -1, null, null, null);//无参的构造方法,默认数据值为0,高度为-1
}
//如果树中节点有变动,从底向上逐级调用该函数,用于更新节点的高度
private int getHight(Node x){
if(x == null){//如果是空结点
return 0;//高度是0
}else{//否则
return x.h;//返回树高
}
}
public int size(){//返回当前树的结点数
return size;//size为结点数
}
//逆时针旋转,X表示轴结点,即第一个结点,RR情况
private void rrRotate(Node X){
Node P = X.parent;//p是第一个结点的上一个结点
Node XR = X.right;//X是第一个节点,XR是第二个结点(即第一个结点的右孩子)
if(P.left == X){//如果当前结点是上一个结点的左孩子
P.left = XR;//那么之前的第二个结点也要作为P的左孩子
}else{//否则
P.right = XR;//作为右孩子
}
XR.parent = P;//XR是最新的子树的根结点,所以要设置此子树根结点的父结点
X.right = XR.left;//把XR的左孩子作为X的右孩子
if(XR.left != null){//如果XR有左孩子的话
XR.left.parent = X;//设置XR的左孩子的父结点
}
XR.left = X;//设置XR左孩子为之前的第一个结点
X.parent = XR;//设置之前第一个结点的父结点为XR
//旋转后要更新这两个节点的高度
X.h = max(getHight(X.left), getHight(X.right)) + 1;
XR.h = max(getHight(XR.left), getHight(XR.right)) + 1;
}
//顺时针旋转(右旋),参数表示轴节点,LL情况
private void llRotate(Node X){//类似上面的RR情况
Node P = X.parent;//p是第一个结点的上一个结点
Node XL = X.left;//X是第一个节点,XL是第二个结点(即第一个结点的左孩子)
if(P.left == X){//如果当前结点是上一个结点的左孩子
P.left = XL;//那么之前的第二个结点也要作为P的左孩子
}else{//否则
P.right = XL;//作为右孩子
}
XL.parent = P;//XL是最新的子树的根结点,所以要设置此子树根结点的父结点
X.left = XL.right;//把XL的右孩子作为X的左孩子
if(XL.right != null){//如果XL有右孩子的话
XL.right.parent = X;//设置XL的右孩子的父结点
}
XL.right = X;//设置XL右孩子为之前的第一个结点
X.parent = XL;//设置之前第一个结点的父结点为XL
/*旋转后要更新这两个节点的高度*/
X.h = max(getHight(X.left), getHight(X.right)) + 1;
XL.h = max(getHight(XL.left), getHight(XL.right)) + 1;
}
public void insert(int in){//插入的方法
insert0(root.right, in);//从根节点开始插入
}
private void insert0(Node x, int in){//从x结点开始插入
if(x == null){//如果找到叶子结点以下,即空结点
root.right = new Node(in, 1, null, null, root);//根节点
size++;//插入一个元素后,树中结点数要+1
return;//插入元素结束
}
if(in - x.element > 0){//要往当前结点的右孩子方向插入
if(x.right != null){//如果该结点的右子树存在,则进行以下操作,否则到else操作去生成新结点
insert0(x.right, in);//递归调用
int lh = getHight(x.left);//递归调用插入后,要计算左孩子的高度,以便检查平衡
int rh = getHight(x.right);//递归调用插入后,要计算右孩子的高度,以便检查平衡
if(rh - lh == 2){//如果不平衡,且右子树更高
if(in - x.right.element > 0){//判断是什么类型
rrRotate(x);//RR类型
}else{//RL类型情况时,要先L后R
llRotate(x.right);//LL
rrRotate(x);//RR
}
}
}else{//直到已经到达叶子结点以下,进行生成一个新结点,从而插入新结点
size++;//结点个数加1
x.right = new Node(in, 1, null, null, x);//插在当前叶子结点的右边
}
}else if(in - x.element < 0){//要往当前结点的左孩子方向插入
if(x.left != null){//如果该结点的左子树存在,则进行以下操作,否则到else操作去生成新结点
insert0(x.left, in);//递归调用
int lh = getHight(x.left);//递归调用插入后,要计算左孩子的高度,以便检查平衡
int rh = getHight(x.right);//递归调用插入后,要计算右孩子的高度,以便检查平衡
if(lh - rh == 2){//如果不平衡,且左子树更高
if(in - x.left.element < 0){//判断是什么类型
llRotate(x);//LL类型
}else{//LR类型情况时,要先R后L
rrRotate(x.left);//RR
llRotate(x);//LL
}
}
}else{//直到已经到达叶子结点以下,进行生成一个新结点,从而插入新结点
size++;//结点个数加1
x.left = new Node(in, 1, null, null, x);//插在当前叶子结点的左边
}
}else{//当前结点值和待插入元素的值相等,用新值覆盖旧值
x.element = in;
}
x.h = max(getHight(x.left), getHight(x.right)) + 1;//更新当前x结点的高度
}
public int max(int a, int b){//求两个参数中的最大值
return a > b ? a : b;//用到了三元运算符
}
public void importFile() throws FileNotFoundException {//读取数据方法
File file = new File("AVL树测试数据.txt");//数据文件名
int i = 0;//接受每一个文件的变量
if(file.exists()){//如果文件存在才读入数据
Scanner input = new Scanner(file);//用于输入
while(input.hasNext()) {//如果文件下一行还有内容
i = Integer.parseInt(input.next());//把读入的字符串变成数字
insert(i);//把读入的数字进行插入
}
input.close();//关闭文件
}
System.out.println("数据读取成功!");//输出提示
}
public double ASL() throws FileNotFoundException {//求平均查找长度的方法
File file = new File("AVL树测试数据.txt");//数据文件名
int i = 0;//接受每一个文件的变量
int sum = 0;//求总的查找次数
int num = 0;//求总结点个数
if(file.exists()){//如果文件存在才读入数据
Scanner input = new Scanner(file);//用于输入
while(input.hasNext()) {//如果文件下一行还有内容
i = Integer.parseInt(input.next());//把读入的字符串变成数字
Node t = root.right;//设置真正的根节点
while(t != null){//当当前结点不为空时,才能进行查找
if(i < t.element){//如果要查找的值,比当前结点值小
t = t.left;//就向左查找
sum++;//把查找次数+1
}else if(i > t.element){//如果要查找的值,比当前结点值大
t = t.right;//就向右查找
sum++;//把查找次数+1
}else {
break;//要查找的值和当前结点值相等,即找到了,就不再继续寻找
}
}
num++;//把查找的结点数+1
}
input.close();//关闭文件
}
return (sum + num) * 1.0 / num;//求平均查找长度的公式,要注意如果一开始就找到了,
//那么这个数的查找长度是1,而不是0
}
public static void main(String[] args) throws FileNotFoundException{
AVLTree avl = new AVLTree();
avl.importFile();
System.out.println("平均查找长度:" + avl.ASL());
}
}