KNN(K最近邻)分类算法个人总结
最近刚刚开始入门机器学习,打算把学过的东西做一个总结,以便日后的查阅。本人还属于小白阶段,这篇总结难免会出现错误,新手上路,请大佬多多指教。
KNN定义
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
KNN算法原理
算法简介
用官方的话来说,所谓K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例, 这K个实例的多数属于某个类,就把该输入实例分类到这个类中。
下面看一个简单的例子:
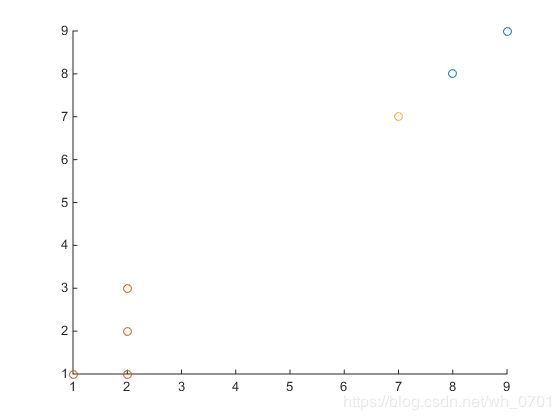
如图所示,红色和蓝色是已经确定的两个类,现在要计算黄色的属于哪一类?
根据上面的介绍,当k取3的时候,最接近的三个点中有两个都属于蓝色类,所以我们可以得出,黄色的点属于蓝色的可能性最大。
距离公式
常见的距离公式计算为欧式距离,欧式距离就是计算两点之间的长度,如上面的例子,两点间的距离可以表示成:
d = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 . d = \sqrt{(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}}. d=(x1−y1)2+(x2−y2)2.
扩展到n维向量,距离表示为:
d = ∑ i = 1 N ( x i 1 − y i 1 ) 2 d=\sqrt{\sum_{i=1}^{N}(x_{i1}-y_{i1})^{2}} d=i=1∑N(xi1−yi1)2
算法步骤
KNN主要步骤如下:
- 计算已知类别数据集中的点与当前点之间的距离
- 按照距离递增次序排序; 选取与当前点距离最小的k个点
- 确定前k个点所在类别的出现频率
- 返回前k个点所出现频率最高的类别作为当前点的预测分类
算法实例
例子均来源于《机器学习实战》,代码基于python3.7
实例1:电影类别分类
| 电影名称 | 打斗镜头 | 接吻镜头 | 电影类别 |
|---|---|---|---|
| 电影1 | 3 | 104 | 爱情片 |
| 电影2 | 2 | 100 | 爱情片 |
| 电影3 | 1 | 81 | 爱情片 |
| 电影4 | 101 | 10 | 动作片 |
| 电影5 | 99 | 5 | 动作片 |
| 电影6 | 98 | 2 | 动作片 |
| ? | 18 | 90 | 未知 |
根据已知电影的类型来推测“?”这部电影所属于的类型
导入数据
由于数据量较少,我们可以直接输入
import numpy as np
def create_data():
group=np.array([
[3,104],
[2,100],
[1,81],
[101,10],
[99,5],
[98,2]
])
labls=['爱情片','爱情片','爱情片','动作片','动作片','动作片']
return group,labls
使用numpy模块,方便之后的计算
计算距离
首先我们要计算出当前点与已知点之间的距离,为了方便计算,我们使用了一些numpy模块中的某些函数
思路:
1、计算当前点各个元素与已知数据集中相对应的元素的差值,为了方便,我们把当前点这个向量复制数量集的个数倍,之后利用矩阵减法就可以一次性完成。所需要的函数如下:
shape函数
shape函数用于返回改数组的维度,如对上文中的group变量使用shape函数将会返回

表示改数组为6行2列的数组,我们需要的是数组的个数,就只要返回shape[0]即可。
tile(A,reps)函数
该函数有两个参数,第一个为被复制的数组,第二个为复制次数,它是元组的形式,第一个元素表示行复制次数,第二个元素表示列复制次数。根据我们的需求,数组A需要在行上复制多次,列只需要复制一次。代码如下:
x=np.tile(A,(6,1))
2、求差之后为一个6行2列的数组,按公式,之后要将数组内的各个元素依次平方,再将每一行求和得到一个6行1列的新数组,最后各个元素开方得到最终距离d。所需要的函数如下:
元素求平方,开根号
a = np.array([1,4,9,16])
print (a)
print (a**2)
print(a**0.5)
矩阵行求和 .sum(axis=1)
该函数可以将数组每行各个元素求和
a = np.array([
[1,2,3],
[4,5,6],
[7,8,9]
])
print(a.sum(axis=1))
距离排序
上一步运算求出了当前点和其他已知点之间的距离,之后就是要排序挑选出前k个点所属于的类,并将占比最大的那个作为结果输出。
如果直接对距离数组进行排序,那么将会改变元素的相对位置,从而使数组无法对应最初的label数组,导致混乱。所以我们可以采用numpy模块中的argsort函数返回数组排序后的索引值,从而不会改变数组之间的位置关系。
x = np.array([3, 1, 2])
print(np.argsort(x))
print(x)
输出结果如下:

返回的是排好序后的索引值,并不会改变原始数组。
之后我们按照索引数组的前k项依次查找他们所对应的类别出现的次数。可以事先定义好一个字典,它的键代表类别名称,值代表这个类别出现的次数。每当一个类别进入该字典时,如果该字典中不存在此键值,就令该值为0,如果存在,则令它对应的值+1重新赋值。
这里我们可以采用字典中的get函数
dict.get(key, default=None)
第一个参数为查找的键值,第二个参数为键值不存在的时候默认返回值。
查找完毕后进行排序,选择最大值所对应的键值输出。排序算法选择python自带的sorted()函数
sorted(iterable[, cmp[, key[, reverse]]])
iterable – 可迭代对象。
cmp – 比较的函数,这个具有两个参数,参数的值都是从可迭代对象中取出,此函数必须遵守的规则为,大于则返回1,小于则返回-1,等于则返回0。
key – 主要是用来进行比较的元素,只有一个参数,具体的函数的参数就是取自于可迭代对象中,指定可迭代对象中的一个元素来进行排序。
reverse – 排序规则,reverse = True 降序 , reverse = False 升序(默认)。
对于本例而言,函数中参数选择为:
A=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
最后返回A[0][0]即为最终结果
具体代码
综上,KNN算法的具体代码实现如下:
import numpy as np
import operator as op
def create_data():
group=np.array([
[3,104],
[2,100],
[1,81],
[101,10],
[99,5],
[98,2]
])
labls=['爱情片','爱情片','爱情片','动作片','动作片','动作片']
return group,labls
'''
inx为要测试的向量
dataset为确认过的数据集
labls为数据集对应的类别
k为选择最邻近的邻居数
'''
def KNN(inx,dataset,labls,k):
datasize=dataset.shape[0] #数据集个数
Mat=np.tile(inx,(datasize,1))-dataset #计算(x1-x2)
Mat=Mat**2 #计算(x1-x2)^2
d2=Mat.sum(axis=1) #计算(x1-x2)^2+(y1-y2)^2
d=d2**0.5 #计算√((x1-x2)^2+(y1-y2)^2)
sortindex=d.argsort() #排序后的索引值
classcount={} #存放类别和次数的字典
for i in range(k):
templabls=labls[sortindex[i]] #第i小的距离所对应的类别
classcount[templabls]=classcount.get(templabls,0)+1 #如果该类别已经在字典中,自增后重新赋值,若不存在则存入1
sortclass=sorted(classcount.items(),key=op.itemgetter(0),reverse=True) #按键值出现次数排序
return sortclass[0][0]
if __name__=='__main__':
x=[18,90]
group,labls=create_data()
print(KNN(x,group,labls,3))
手写数字识别
数据来源机器学习实战-图书-图灵社区
随书附带的源码Ch02/digits.zip压缩文件中
数据导入
书中给出的数据为txt文件格式,内容如下所示:
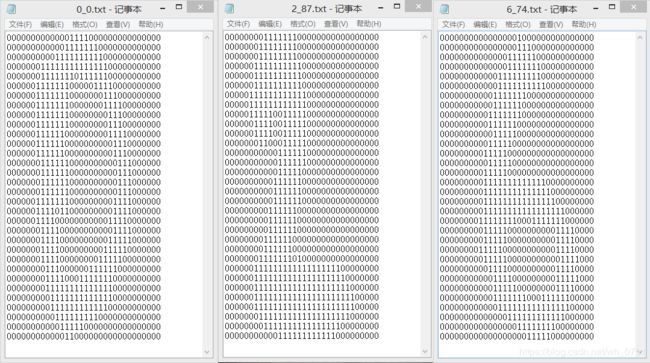
为了使用上面所写的分类器需要把这些01字符串转换成向量的形式。
每一个文件都是32*32的形式,我们可以把他们转换成一个1*1024的向量,这样就可以用上面所写的函数处理信息了。
我们可以事先创立好一个1*1024的空数组,然后打开相应的文件,循环读出32行,每一行读前32个字符,把他们转换成整形并输入到数组中。主要代码如下:
def img2vector(fname):
v=np.zeros((1,1024)) #一个1*1024的0向量
with open(fname) as f: #打开对应的文件
for i in range(32): #依次读取前32行32列的数据
linestr=f.readline()
for j in range(32):
v[0,32*i+j]=int(linestr[j]) #字符转换成整形
return v
注意到文件的命名都是有规律的

以‘_’作为分界符,前面是对应的数字,后面是样例的序号,可以通过处理文件名来获得该文件对应的数字。
涉及的函数如下:
str.split(str="", num=string.count(str)).
第一个参数为分隔符,本例中为‘_’。获取对应的数字代码为:
classnum=str.split('_')[0]
这样就可以获取到该样本所对应的数字了。
os.listdir(path)
该方法用于返回指定的文件夹包含的文件或文件夹的名字的列表。用此方法可以遍历文件夹中的所有txt文件,进行循环处理。
至此就可以完成数据导入工作,代码如下:
def create_data():
labels=[] #类别数组
flist=os.listdir('trainingDigits') #获取文件列表
l=len(flist)
train_dataset=np.zeros((l,1024)) #训练数据集合
for i in range(l):
fname=flist[i]
classnum=int(fname.split('_')[0])
labels.append(classnum)
train_dataset[i,:]=img2vector('trainingDigits/%s' % fname)
return train_dataset,labels
数据处理
在成功导入数据之后,就需要对测试数据进行检测,观察算法的正确性如何。主要代码如下:
def test_number():
td,tl=create_data()
tlist=os.listdir('testDigits')
l=len(tlist)
error_count=0
for i in range(l):
fname=tlist[i]
right_num=int(fname.split('_')[0])
test_vector=img2vector('testDigits/%s' % fname)
result_num=KNN(test_vector,td,tl,3)
print('正确结果是:%d,程序得出结果是:%d' % (right_num,result_num))
if(right_num!=result_num):
error_count+=1
print('错误个数为:%d' % error_count)
print('错误率为:%f' % (float(error_count)/float(l)))
总结
kNN算法的优缺点
优点
简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;
可用于数值型数据和离散型数据;
训练时间复杂度为O(n);无数据输入假定;
对异常值不敏感
缺点
计算复杂性高;空间复杂性高;
样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
一般数值很大的时候不用这个,计算量太大。但是单个样本又不能太少,否则容易发生误分。
最大的缺点是无法给出数据的内在含义。

