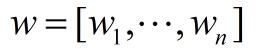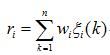灰色关联分析——供应商选择
笔记来源链接:https://www.toutiao.com/i6818467436493275659/
本笔记根据清风老师的课程以及《数学建模算法与应用》整理学习得到,如有侵权,请联系删除。
灰色关联分析思维导图:
灰色加权关联度(增加了权重)
灰色关联分析原理
灰色关联分析方法是基于灰色系统理论发展而来的一种综合评价和影响因素分析方法。
基本思想:通过对动态过程发展趋势进行量化分析,完成对系统内时间序列有关统计数据几何关系的比较,求出参考数列(子序列,类似于自变量)与比较数列(母序列,类似于因变量)之间的灰色关联度。按关联度的大小对各指标进行排序,确定关联序,通过关联度和关联序分析比较数列指标变化对参考数列指标的影响程度。
参考文献:翟广倩, 段利忠. 基于灰色关联的综合医院中医药发展影响因素分析[J]. 卫生软科学, 2019(10).
灰色关联分析具体步骤
1. 确定比较对象和参考数列假设评价对象有m个,评价指标有n个。
参考数列为:
![]()
参考数列(母序列)
需要特别注意,当灰色关联分析用于综合评价时,母序列需要自己虚构,虚构的母序列(参考数列)是每行的最大值(假设行表示评价对象,列表示评价指标)。
比较数列为:
![]()
比较数列(母序列)
2. 指标正向化处理常见的四种指标为极大型指标(效益型指标)、极小型指标、中间型指标和区间型指标。指标正向化一般是指将后面三种指标转为极大型指标。
(1)极小型指标正向化
极小型指标:值越小对评价越有利的指标,比如折扣,和别人的争吵次数等
极小型指标正向化公式
一般比较常用的是第一种,用该指标中的最大数减去每一个数。
MATLAB代码:
function [posit_x] = Mid2Max(x,best)
M = max(abs(x-best));
posit_x = 1 - abs(x-best) / M;
end(2) 中间型指标正向化
中间型指标:值处于某个值最好。比如水质量评价中,一般认为PH=7是最好的。
中间型指标正向化公式
function [输出变量] = 函数名称(输入变量)
MATLAB代码:
function [posit_x] = Mid2Max(x,best)
M = max(abs(x-best));
posit_x = 1 - abs(x-best) / M;
end(3)区间型指标正向化
区间型指标:值处于某个范围是最好的。比如人的体温在36-37.5度是认为比较健康的。
区间型指标正向化
matlab代码实现:
function [posit_x] = Inter2Max(x,a,b)
r_x = size(x,1); % row of x
M = max([a-min(x),max(x)-b]);
posit_x = zeros(r_x,1); %zeros函数用法: zeros(3) zeros(3,1) ones(3)
% 初始化posit_x全为0 初始化的目的是节省处理时间
for i = 1: r_x
if x(i) < a
posit_x(i) = 1-(a-x(i))/M;
elseif x(i) > b
posit_x(i) = 1-(x(i)-b)/M;
else
posit_x(i) = 1;
end
end
end3.指标标准化处理标准化的目的是消除不同指标间的量纲化。也就是取出单位、数字的大小等的影响,让所有指标在一个维度里面进行分析处理。
比重法
【注意】标准化的方法有很多种,其主要目的就是去除量纲的影响,未来我们还可能见到更多 种的标准化方法,例如:(x‐x的均值)/x的标准差;具体选用哪一种标准化的方法在多数情况下 并没有很大的限制,这里我们采用的是前人的论文中用的比较多的一种标准化方法。
离差标准化
MATLAB代码实现:
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1)4. 确定各指标对应的权重确定权重主观的方法可以用层次分析法,可以看之间的笔记。
数学建模竞赛学习笔记:层次分析法及其代码实现
客观的方法有熵值法、因子分析法等等,后面会一一更新求解方法。客观求权重的模型对数据要求比较高,如果有些指标可以找到数据,有些指标属于是定性指标,无法找到数据,就可以使用层次分析法和熵值法等进行组合求解(组合求权重)。
指标权重也可以根据各个指标与参考数列之间的关系
各个指标的权重,wn为第n个指标的权重
5. 计算灰色关联系数两级最小差
两级最大差
分辨系数:
![]()
【注意】一般来说,分辨系数越大,分辨率越大;分辨系数越小,分辨率越小。
灰色关联系数:(为标记数列xi对参考数理x0在第k个指标上的关联系数)
6. 计算灰色加权关联度灰色关联度的计算公式为:
其中:ri为第i个评价对象对理想对象的灰色加权关联度。
7. 评价分析根据灰色加权关联度的大小,对各评价对象进行排序,可建立评价对象的关联序,关联度越大,其评价效果越好。
供应商选择决策MATLAB代码实现
例题来自《数学建模算法与应用 司守奎》。
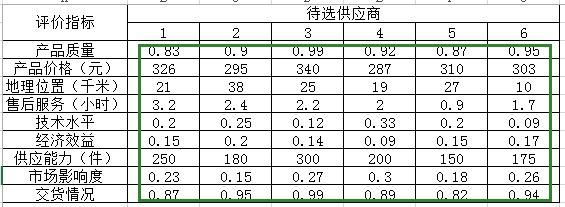
某核心企业需要在6个待选的零部件供应商中选择一个合作伙伴,各个供应商的数据如下表所示:
(1)将绿色框中的数据复制粘贴到MATLAB中
数据导入
(2)输入代码(标准化采用离差标准化)
load data.mat
%% 指标正向化、标准化处理
for i = [1 5:9]%效益型指标标准化,1、5、6、7、8、9行标准化
a(i,:) = (a(i,:) - min(a(i,:)))/(max(a(i,:))-min(a(i,:)))
end
for i = 2:4%成本型指标标准化 2、3、4行标准化
a(i,:) = (max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)))
end
[m,n] = size(a);
%% 求灰色关联系数
cankao = max(a')' % 求参考序列的取值
t = repmat(cankao,[1,n])-a; %求参考序列与每一个序列的差
mmin = min(min(t));%计算最小差
mmax = max(max(t));%计算最大差
rho = 0.5; %分辨系数
xishu = (mmin + rho*mmax)./(t+rho*mmax)%计算灰色关联度
%% 求灰色关联度
guanliandu = mean(xishu);%取等权重,计算关联度
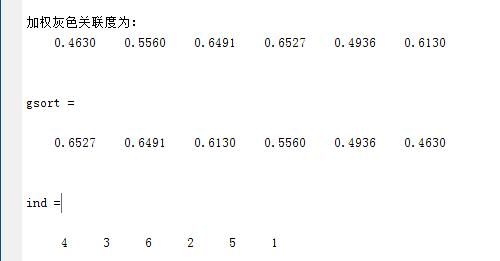
disp('加权灰色关联度为:')
disp(guanliandu)
[gsort,ind] = sort(guanliandu,'descend')%将关联度从大到小排序(3)结论
可以得到第1-6个供应商的加权灰色关联度为0.4630、 0.5560 、0.6491 、0.6527 、0.4936 、0.6130。按照灰色关联度排序可以看出,供应商4与虚拟最优供应商的关联度最大,所以应该选择供应商4会达到最优解。