牛客网暑期ACM多校训练营(第十场)D Rikka with Prefix Sum
链接:https://www.nowcoder.com/acm/contest/148/D
来源:牛客网
题目描述
Prefix Sum is a useful trick in data structure problems.
For example, given an array A of length n and m queries. Each query gives an interval [l,r] and you need to calculate . How to solve this problem in O(n+m)? We can calculate the prefix sum array B in which Bi is equal to . And for each query, the answer is Br-Bl-1.
Since Rikka is interested in this powerful trick, she sets a simple task about Prefix Sum for you:
Given two integers n,m, Rikka constructs an array A of length n which is initialized by Ai = 0. And then she makes m operations on it.
There are three types of operations:
1. 1 L R w, for each index i ∈ [L,R], change Ai to Ai + w.
2. 2, change A to its prefix sum array. i.e., let A' be a back-up of A, for each i ∈ [1,n], change Ai to ![]() .
.
3. 3 L R, query for the interval sum .
输入描述:
The first line contains a single number t(1≤ t ≤ 3), the number of the testcases.
For each testcase, the first line contains two integers n,m(1 ≤ n,m ≤ 105).
And then m lines follow, each line describes an operation(1 ≤ L ≤ R≤ n, 0 ≤ w ≤ 109).
The input guarantees that for each testcase, there are at most 500 operations of type 3.输出描述:
For each query, output a single line with a single integer, the answer modulo 998244353.
示例1
输入
复制
1
100000 7
1 1 3 1
2
3 2333 6666
2
3 2333 6666
2
3 2333 6666
输出
复制
13002
58489497
12043005题意:长度为n的数组,初始值都为0,操作1 将L R区间的数增加w,操作2将数组求一次前缀和,操作3 输出L R区间的数之和
思路:一开始考虑线段树,因为输出最多500次,所以考虑只在输出的时候求前缀和,前面的求前缀和记录下来,但是由于还有区间增加操作,所以一直没能处理好。赛后看别人代码是组合数, 一脸懵逼,然后看了看自己的草稿,看了看杨辉三角的组合数的图,才醒悟。
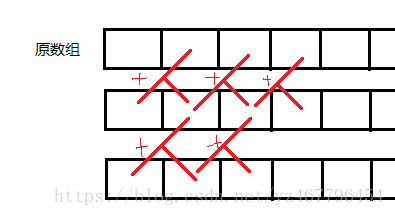
首先,图一是杨辉三角,图二是多次求前缀和的过程,前缀和数组当前位=原数组当前位+前缀和数组前一位,如果这样不够清楚的话,可以将你的头往左边旋转45°来看。
所以,当遇到操作1时,记录l r w 还有当前的2操作个数,当遇到2操作时,2操作数增加,遇到3操作时,可以通过组合数求得答案。
但是呢,就算你知道了要用组合数求,后面思考还是很麻烦的,我没怎么想明白,这篇博客写的挺好的,可以参照2018牛客网暑假ACM多校训练赛(第十场)D Rikka with Prefix Sum 组合数学,主要是取反前缀这边比较难理解。
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int maxn=200005;
ll mo(ll a,ll pp){
if(a>=0&&a>=1,a=mo(a*a,pp)){
if(b&1)ans=mo(ans*a,pp);
}
return ans;
}
ll b[maxn],invf[maxn],inv[maxn];
ll C(int n,int m){
if(n