使用数字示波器DS6104测量交流信号的幅值和相位

 

01简介

---

使用普通的万用表测量交流信号的时候，通常会遇到 万用表的频率响应 的问题。使用可以联网的示波器可以获得它采集到的数据，进而可以计算出所测量的交流信号的有效值和相位。

这里通过实验来确定使用示波器测量交流信号的参数方法中的以下问题：

• 测量的精度有多高？ 测量的频率范围有多宽？
• 获得高精度的测量参数，对于示波器参数如何设置？

^{▲ 实验所使用的示波器：ds6104}

实验所使用的DS6104是一款可以通过联网读取各通道采集数据的示波器，为自动化测量提供了很好的支持。对它的 DS6104局域网络编成接口 可以从网络中下载相关的文档。

DS6104对于每个通道采样数据点个数$N=1400$，采样的有效位数为8bit。下面显示了DS6104采集一个有效值为$E=2.39V$，频率为$f=1000Hz$的正弦波波形。该信号是由 DS345 信号发生器产生。该信号发生器同时还可以产生同相的同步方波信号，可以便于示波器用于同步采集信号的波形。

^{▲ 通过DS6104读取的信号发生器所产生的1000Hz信号及其同步方波信号}

 

02测量方法

---

假设被测量信号的频率为$f$，有效值为$E$，那么信号的表达式为：$$f\left(t\right)=\sqrt{2}\cdot E\cdot \sin \left(2\pi f\cdot t+\theta \right)$$示波器采样时间间隔为$T_s$，采样点个数$N$。所得到的采样数据为：$$f\left[n\right]=\sqrt{2}\cdot E\cdot \sin \left(2\pi f\cdot n{T}_s+\theta \right),n=0,1,...,N-1$$

从数据中计算信号的$E,\theta$，采用以下方法。首先计算序列与$\cos \left[n{T}_s\right],\sin \left[n{T}_s\right]$的投影（内积）：
$$Y_s=\frac{1}{N}\sum _{n=0}^{N-1}f\left[n\right]\cdot \sin \left(2\pi f\cdot n{T}_s\right)$$$$Y_c=\frac{1}{N}\sum _{n=0}^{N-1}f\left[n\right]\cdot \cos \left(2\pi f\cdot n{T}_s\right)$$

将上述两个公众是的$f\left[n\right]$代入，并进行化简。对于$Y_s$可以化简如下：
$$Y_s=\frac{1}{N}\sum _{n=0}^{N-1}\sqrt{2}\cdot E\cdot \sin \left(2\pi f\cdot n{T}_s+\theta \right)\cdot \sin \left(2\pi f\cdot n{T}_s\right)$$$$=\frac{\sqrt{2}\cdot E}{N}\sum _{n=0}^{N-1}\frac{1}{2}\left[\cos \left(\theta \right)-\cos \left(4\pi f\cdot n{T}_s+\theta \right)\right]$$$$=\frac{E}{\sqrt{2}}\cos \left(\theta \right)+\frac{E}{\sqrt{2}\cdot N}\sum _{n=0}^{N-1}\cos \left(4\pi f\cdot n{T}_s+\theta \right)$$

根据 等差角度cos，sin序列之和公式 ：
$$\sum _{n=0}^{N-1}\cos \left(a+nd\right)=R\cdot \cos \left[a+\left(N-1\right)\frac{d}{2}\right]$$$$\sum _{n=0}^{N-1}\sin \left(a+nd\right)=R\cdot \sin \left[\alpha +\left(N-1\right)\frac{d}{2}\right]$$

其中：$$R=\frac{\sin \left(\frac{N\cdot d}{2}\right)}{\sin \left(\frac{d}{2}\right)}$$

当$\sin \left(\frac{d}{2}\right)=0$时，$R=N$。
对于前序列采样公式，$d=4\pi f\cdot T_s$，N=1400。下面假设f=1，对ts取不同值绘制出R对应的曲线：

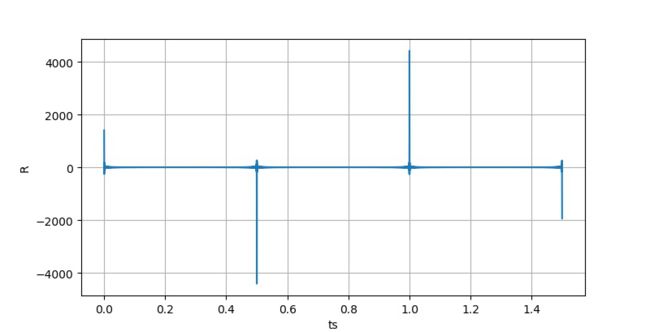
^{▲ ts的不同取值下的R的取值，其中N=1400}

可以看出，当ts取(0.5)整数倍数的时候，对应的R值很大。当ts偏离(0.5)整数倍数时，R迅速减少。下面给出Ts取0~0.之间的值对应的R的曲线：

^{▲ ts取值0~0.1之间的数值时对应的R取值}

^{▲ ts取值0.45~0.55之间时，对应的R的取值}

从上面分析可以看出，当ts取值范围在$0.1\frac{1}{f}$到$0.45\frac{1}{f}$之间时，对应正弦波每个周期采样点在2.5~10之间，R的取值都会远远小于N。因此，$Y_s$就可以近似为：
$$Y_s\approx \frac{E}{\sqrt{2}}\cos \left(\theta \right)$$

同样的分析可以知道：$$Y_c\approx \frac{E}{\sqrt{2}}\sin \left(\theta \right)$$

然后在计算信号的幅值和相位：
$$E=\sqrt{2}\cdot \sqrt{Y_s^2+Y_c^2}$$
$$\theta =\arctan \left(\frac{Y_c}{Y_s}\right)$$

def data2ap(tt, y, freq):
    sint = [sin(t * 2 * pi * freq) for t in tt]
    cost = [cos(t * 2 * pi * freq) for t in tt]
    ys = sum([a * b for a,b in zip(y, sint)]) / len(tt)
    yc = sum([a * b for a,b in zip(y, cost)]) / len(tt)
    amp = sqrt(ys**2 + yc**2)*sqrt(2)
    phase = atan2(ys,yc)
    return amp,phase

通过对一个1000Hz测试正弦波的测量，所获得的测量结果为：E=2.4382V, $\theta =1.3108$。
示波器的设置：时基时间T$Tb=500\mu s$，幅值尺度$V_b=2V$。

使用FLUKE45数字万用表的交流档测量该交流信号的有效值为：$E_f=2.394V$。可以看出与示波器所测得得到的结果之间有1.85%的误差。

 

03测量性能

---

1.测量数值精度

测量100次信号的幅值和相位，统计相应的平均值和方差：

• 幅值：$E_{mean}=2.4383V,Var\left(E\right)=3.51\times 10^{-7}$
• 相位：${\theta }_{mean}=1.3112,Var\left(\theta \right)=6.2134\times 10^{-8}$
  ^{▲ 测量100个数据的分布}

2.示波器时基长度对测量结果的影响

（1）直接采集信号进行测量

设置示波器的时基参数，可以改变数据采集时间间隔，同时也影响了每帧数据（对于DS6104，数据长度为1400）对应信号的周期个数。

^{▲ 不同时基下采集到的信号波形}

下面显示了对于时基信号从30us变化到5000us过程中，200个信号的幅值和相位的测量数据。

^{▲ 不同的时下测量幅度和相位的变化}

在上面分析由于不同时基的变化，对应采样时间的变化对于测量结果的影响，在ts小于0.002秒之前似乎还能够通过理论分析得到这个结果。但是对于ts大于0.002秒之后的这种变化，感觉就无法从理论上来分析了。

在博文 对示波器测量正弦波幅值和相位仿真实验 中通过理论仿真来验证不同时基ts下的测量误差，可以看到在前面ts大于0.002秒之后的部分的确不在理论可以分析的范围之内。所以这部分误差需要在实际测量中加以避免。

a=[2.13,2.84,2.27,2.40,2.60,2.32,2.45,2.52,2.35,2.47,2.48,2.36,2.48,2.45,2.37,2.48,2.44,2.39,2.48,2.42,2.41,2.48,2.41,2.43,2.47,2.40,2.41,2.45,2.40,2.44,2.43,2.38,2.44,2.44,2.41,2.42,2.41,2.40,2.45,2.42,2.42,2.43,2.40,2.42,2.45,2.42,2.40,2.43,2.40,2.43,2.45,2.38,2.42,2.43,2.41,2.44,2.40,2.39,2.43,2.42,2.42,2.45,2.39,2.40,2.44,2.42,2.43,2.41,2.40,2.42,2.43,2.42,2.40,2.41,2.40,2.43,2.43,2.43,2.41,2.40,2.24,2.40,2.24,2.37,2.24,2.36,2.20,2.37,2.18,2.34,2.42,2.32,2.42,2.32,2.40,2.31,2.40,2.28,2.41,2.27,2.38,2.25,2.38,2.22,2.38,2.21,2.36,2.20,2.34,2.17,2.34,2.41,2.32,2.41,2.30,2.41,2.30,2.39,2.28,2.39,2.25,2.39,2.24,2.37,2.23,2.36,2.20,2.36,2.18,2.34,2.17,2.32,2.41,2.32,2.40,2.30,2.40,2.27,2.40,2.27,2.38,2.25,2.37,2.22,2.38,2.21,2.35,2.19,2.34,2.16,2.34,2.41,2.32,2.41,2.29,2.41,2.29,2.39,2.27,2.39,2.25,2.39,2.23,2.37,2.22,2.36,2.19,2.35,2.17,2.33,2.15,2.32,2.41,2.31,2.40,2.29,2.40,2.27,2.40,2.26,2.38,2.24,2.37,2.21,2.37,2.20,2.35,2.18,2.34,2.15,2.33,2.13,2.31,2.41,2.29,2.41,2.29,2.38,2.26,2.40]
p=[1.06,1.32,1.15,1.20,1.28,1.17,1.25,1.23,1.20,1.26,1.29,1.28,1.26,1.23,1.31,1.28,1.22,1.31,1.28,1.36,1.31,1.28,1.36,1.31,1.28,1.36,1.36,1.32,1.25,1.22,1.46,1.40,1.36,1.31,1.25,1.50,1.45,1.40,1.36,1.31,1.26,1.49,1.45,1.40,1.36,1.30,1.55,1.50,1.45,1.40,1.36,1.59,1.38,1.33,1.28,1.23,1.46,1.41,1.37,1.31,1.25,1.21,1.45,1.39,1.34,1.29,1.24,1.48,1.42,1.37,1.32,1.27,1.51,1.46,1.40,1.36,1.30,1.25,1.49,1.37,1.76,1.40,1.81,1.47,1.85,1.52,1.90,1.56,1.95,1.61,1.28,1.64,1.32,1.71,1.37,1.75,1.42,1.81,1.47,1.85,1.51,1.90,1.56,1.95,1.59,2.00,1.66,2.03,1.71,2.09,1.75,1.41,1.80,1.46,1.83,1.51,1.89,1.54,1.94,1.61,1.99,1.65,2.04,1.70,2.07,1.75,2.14,1.79,2.18,1.84,2.22,1.48,1.14,1.53,1.18,1.56,1.22,1.61,1.27,1.65,1.31,1.69,1.35,1.73,1.39,1.77,1.43,1.84,1.47,1.86,1.52,1.17,1.55,1.22,1.60,1.26,1.64,1.30,1.68,1.35,1.73,1.38,1.77,1.47,1.80,1.46,1.85,1.51,1.89,1.55,1.95,1.59,1.25,1.63,1.29,1.67,1.34,1.71,1.37,1.75,1.42,1.79,1.45,1.86,1.49,1.88,1.54,1.92,1.58,1.96,1.62,2.01,1.66,1.33,1.70,1.36,1.85,1.41,1.79,1.45]
tbase=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.01]

（2）通过加窗方法进行测量

对采集数据通过加窗处理，可以避免由于对数据的截断所引起的频率特性的波动，进而提高对信号测量的精度。

常用到的窗口包括有三角波窗口，升余弦（Hanning）窗口等。

^{▲ 三角窗口与升余弦（Hanning）窗口}

下面是统一正弦波在三角窗口和Hanning窗口加权下的波形。可以看出，经过加窗处理之后，数据在在时域内不再会因为截取而不连续了。

^{▲ 加窗后的数据波形（左：三角窗；右：Haning窗口）}

由于加窗对数据幅度有了改变，所以会直接影响测量的结果。下面显示不同加窗方法处理后的幅度和相位。幅度会因为增加三角窗口和Hanning窗口而减少1倍左右，相位测量不受窗口方法的影响。

窗口	幅度	相位
矩形窗	2.4400	1.4182
三角窗	1.2209	1.4177
汉宁窗	1.2226	1.4175

下面对数据经过加窗处理之后，看示波器的时基大小对测量结果的影响。

A.使用三角窗测量信号的幅度和相位

测量过程中信号经过三角波加窗。

^{▲ 使用三角窗测量信号的幅值和相位}

测量的幅值和相位的结果如下：

^{▲ 使用三角窗测量信号的幅度和相位}

a=[1.71,2.31,2.42,2.36,2.42,2.43,2.41,2.44,2.43,2.42,2.44,2.43,2.43,2.44,2.43,2.43,2.44,2.43,2.43,2.43,2.43,2.44,2.43,2.43,2.44,2.44,2.42,2.43,2.43,2.43,2.42,2.42,2.43,2.43,2.43,2.41,2.42,2.43,2.42,2.43,2.43,2.42,2.42,2.43,2.43,2.43,2.42,2.42,2.43,2.43,2.45,2.41,2.42,2.43,2.43,2.43,2.41,2.42,2.42,2.43,2.43,2.43,2.42,2.42,2.43,2.43,2.43,2.41,2.42,2.42,2.43,2.43,2.41,2.42,2.42,2.43,2.43,2.43,2.42,2.41,2.33,2.40,2.33,2.40,2.32,2.39,2.31,2.39,2.30,2.38,2.41,2.37,2.41,2.37,2.41,2.36,2.41,2.35,2.41,2.34,2.40,2.34,2.40,2.32,2.39,2.31,2.39,2.30,2.38,2.29,2.37,2.41,2.37,2.41,2.36,2.41,2.35,2.41,2.34,2.40,2.33,2.40,2.33,2.40,2.32,2.39,2.31,2.38,2.30,2.38,2.29,2.37,2.41,2.36,2.41,2.36,2.41,2.35,2.41,2.34,2.40,2.33,2.40,2.32,2.39,2.31,2.39,2.30,2.38,2.29,2.37,2.41,2.37,2.41,2.36,2.41,2.35,2.41,2.34,2.41,2.33,2.40,2.32,2.39,2.31,2.39,2.30,2.38,2.29,2.37,2.28,2.37,2.41,2.36,2.41,2.35,2.41,2.34,2.40,2.34,2.40,2.33,2.39,2.32,2.39,2.31,2.38,2.29,2.38,2.28,2.37,2.27,2.36,2.41,2.35,2.41,2.35,2.40,2.34,2.42]
p=[0.66,1.15,1.20,1.17,1.23,1.22,1.24,1.20,1.22,1.25,1.27,1.30,1.25,1.22,1.32,1.27,1.22,1.32,1.27,1.37,1.32,1.27,1.37,1.32,1.27,1.37,1.36,1.31,1.26,1.21,1.45,1.41,1.36,1.31,1.26,1.50,1.45,1.40,1.35,1.31,1.26,1.49,1.45,1.40,1.35,1.31,1.55,1.50,1.45,1.40,1.36,1.59,1.38,1.33,1.28,1.23,1.46,1.41,1.37,1.31,1.26,1.21,1.45,1.39,1.34,1.29,1.24,1.47,1.42,1.37,1.32,1.28,1.51,1.45,1.40,1.36,1.30,1.25,1.49,1.37,1.76,1.40,1.81,1.47,1.85,1.52,1.90,1.56,1.95,1.61,1.28,1.64,1.32,1.71,1.37,1.76,1.42,1.80,1.47,1.85,1.51,1.89,1.56,1.95,1.59,1.99,1.66,2.04,1.70,2.09,1.75,1.42,1.80,1.46,1.82,1.51,1.89,1.54,1.94,1.61,1.99,1.65,2.04,1.70,2.08,1.75,2.13,1.79,2.18,1.84,2.23,1.48,1.14,1.53,1.18,1.56,1.22,1.62,1.27,1.65,1.31,1.69,1.35,1.73,1.39,1.77,1.43,1.84,1.47,1.86,1.52,1.18,1.56,1.22,1.60,1.26,1.64,1.30,1.69,1.35,1.73,1.38,1.77,1.47,1.80,1.46,1.85,1.51,1.89,1.55,1.95,1.59,1.25,1.63,1.29,1.67,1.34,1.71,1.37,1.75,1.42,1.80,1.45,1.86,1.50,1.88,1.54,1.92,1.58,1.96,1.62,2.01,1.66,1.32,1.70,1.36,1.85,1.41,1.79,1.45]
tbase=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.01]

B.使用Hanning窗口加权：

^{▲ 使用Hnning窗测量信号的幅值和相位}

^{▲ 使用Hanning窗测量信号的幅值和相位}

a=[1.67,2.19,2.49,2.45,2.43,2.45,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.44,2.43,2.43,2.43,2.44,2.42,2.43,2.43,2.43,2.44,2.42,2.43,2.43,2.43,2.43,2.44,2.42,2.43,2.43,2.43,2.44,2.42,2.43,2.43,2.43,2.45,2.42,2.43,2.43,2.43,2.43,2.42,2.42,2.43,2.43,2.43,2.44,2.42,2.43,2.43,2.43,2.43,2.42,2.43,2.43,2.43,2.43,2.42,2.42,2.43,2.43,2.43,2.43,2.42,2.41,2.34,2.40,2.35,2.40,2.34,2.40,2.33,2.39,2.33,2.39,2.42,2.38,2.42,2.38,2.41,2.37,2.41,2.36,2.42,2.36,2.41,2.36,2.40,2.35,2.40,2.34,2.40,2.33,2.39,2.32,2.38,2.42,2.38,2.42,2.38,2.41,2.37,2.41,2.36,2.41,2.35,2.40,2.35,2.40,2.34,2.40,2.33,2.39,2.32,2.39,2.32,2.38,2.42,2.38,2.41,2.37,2.41,2.37,2.41,2.36,2.41,2.35,2.40,2.34,2.40,2.34,2.40,2.33,2.39,2.32,2.39,2.42,2.38,2.42,2.37,2.41,2.37,2.41,2.36,2.41,2.35,2.40,2.35,2.40,2.34,2.40,2.33,2.39,2.32,2.39,2.31,2.38,2.42,2.38,2.41,2.37,2.41,2.36,2.41,2.36,2.40,2.35,2.40,2.34,2.40,2.33,2.39,2.32,2.39,2.31,2.38,2.30,2.38,2.41,2.37,2.41,2.37,2.41,2.36,2.42]
p=[0.54,1.09,1.22,1.21,1.23,1.22,1.25,1.20,1.23,1.25,1.27,1.30,1.25,1.22,1.32,1.27,1.22,1.32,1.27,1.37,1.32,1.27,1.37,1.32,1.27,1.37,1.36,1.31,1.26,1.21,1.45,1.41,1.36,1.31,1.26,1.50,1.45,1.40,1.35,1.31,1.26,1.49,1.45,1.40,1.35,1.31,1.55,1.50,1.45,1.40,1.36,1.59,1.38,1.33,1.28,1.23,1.46,1.41,1.37,1.31,1.26,1.21,1.45,1.39,1.34,1.29,1.24,1.47,1.42,1.37,1.32,1.28,1.51,1.45,1.40,1.36,1.30,1.25,1.49,1.37,1.76,1.40,1.81,1.47,1.85,1.52,1.90,1.56,1.95,1.61,1.28,1.64,1.32,1.71,1.37,1.75,1.42,1.80,1.47,1.85,1.51,1.89,1.56,1.95,1.59,1.99,1.66,2.04,1.70,2.09,1.75,1.42,1.80,1.46,1.82,1.51,1.89,1.54,1.94,1.61,1.99,1.65,2.04,1.70,2.08,1.75,2.13,1.79,2.18,1.84,2.23,1.48,1.14,1.53,1.18,1.56,1.22,1.62,1.27,1.65,1.31,1.69,1.35,1.73,1.39,1.77,1.43,1.84,1.47,1.86,1.52,1.18,1.56,1.22,1.60,1.26,1.64,1.30,1.69,1.35,1.73,1.38,1.77,1.47,1.80,1.46,1.85,1.51,1.89,1.55,1.95,1.59,1.25,1.63,1.29,1.67,1.34,1.71,1.37,1.75,1.42,1.79,1.45,1.86,1.50,1.88,1.54,1.92,1.58,1.96,1.62,2.01,1.66,1.32,1.70,1.36,1.85,1.40,1.79,1.45]
tbase=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.01]

C.对比矩形窗、三角窗、Hanning窗的效果

通过对比可以看出，经过加窗处理之后，时基长度小于2ms之内，测量的结果收到时基长度的影响就大大减弱了。

^{▲ 对比矩形窗、三角窗、Hanning窗对于幅度测量的影响}

特别是在时基设置为0.25~0.7毫秒左右（对应1000Hz的信号，示波器显示大约3.5至10个周期）使用Hanning窗口所测量的幅度谱基本上不受时基长短的 影响。

^{▲ 对比矩形窗、三角窗、Hanning窗对于幅度测量的影响(局部)}

#------------------------------------------------------------
def winddata(len, mode = 0):
    if mode == 0:
        return [1] * len
    elif mode == 1:         # Triangle Window
        win = [1] * len
        for i in range(len):
            if i < len / 2:
                win[i] = i / ((len + 1) / 2)
            else: win[i] = (len-i) / ((len + 1) / 2)
        return win
    elif mode == 2:
        win = [1] * len
        for i in range(len):
            theta = (i - (len - 1) / 2) * pi * 2 / len
            win[i] = (1 + cos(theta)) / 2
        return win
    else: return [1] * len
#------------------------------------------------------------
def data2ap(tt, y, freq):
    sint = [sin(t * 2 * pi * freq) for t in tt]
    cost = [cos(t * 2 * pi * freq) for t in tt]
    ys = sum([a * b for a,b in zip(y, sint)]) / len(tt)
    yc = sum([a * b for a,b in zip(y, cost)]) / len(tt)
    amp = sqrt(ys**2 + yc**2)*sqrt(2)
    phase = atan2(ys,yc)
    return amp,phase
#------------------------------------------------------------
def ds6104data(freq, win=0):
    x,y = ds6104readcal(1)
    if win == 1:
        wind = winddata(len(x), 1)
        y = [d * w * 2 for d,w in zip(y, wind)]
    elif win == 2:
        wind = winddata(len(x), 2)
        y = [d*w*2 for d,w in zip(y, wind)]
    a,p = data2ap(x,y,freq)
    return a, p, x, y

 

04示波器采样模式对测量精度的影响

---

示波器采样模式包括有四种：正常采样模式、平均采样模式、峰值采样模式以及高分辨率采样模式。下面通过对比实验，查看这些采样模式对于测量精度的影响。、

下面实验中，采样信号为1000Hz，有效值为2.3V左右的正弦波信号。示波器的时基设为0.7ms，处理数据使用Hanning窗加窗。

1.正常采样模式

测量结果：
幅值：2.44283V；相位：1.29056

^{▲ 正常采样模式下的信号的波形}

2.平均采样模式

测量结果：
幅值：2.44128；相位：1.2282

^{▲ 平均采样模式下信号的波形}

3.峰值采样模式

测量结果：
幅值：2.44415V；相位：1.2903

^{▲ 峰值采样模式下的信号波形}

4.高分辨率采样模式

测量结果：
幅值：2.4243V；相位：1.4068

^{▲ 高分辨率采样模式下的信号波形}

对比以上四种示波器采样模式，对于信号的幅度没有太多的影响，对于信号的相位，高分辨率采样则出现了与其它三类较大的差异。根据示波器实际波形显示，采用高分辨率采样模式所得到的结果与实际相位是最接近的。

采样模式		幅值	相位
1	正常采样	2.44283	1.29056
2	平均采样	2.44128	1.2282
3	峰值采样	2.44415	1.2903
4	高分辨率采样	2.4243	1.4068

 

05不同频率对测量结果的影响

---

对于信号频率从10Hz变化到10MHz，使用相同的方法进行测量它的幅值和相位，结果如下：

频率	幅值	相位
10.0	2.3879	1.3380
100.0	2.4073	1.2545
1000.0	2.4385	1.3111
10000.0	2.5401	1.2231
100000.0	2.5516	1.2740
1000000.0	2.5952	1.0833
10000000.0	2.3971	-0.6503

#------------------------------------------------------------
def ds6104settimebase(freq, period):
    timebase = period / freq / 14
    ds6104timebase(timebase)   

 

06结论

---

通过对DS6104联网示波器采集到的数据进行加窗计算，可以获得被测量信号的幅值和相位。这种方法所得到的数值精度在1000Hz时精度很高。同样，这种方法所能适应的频率范围可以是示波器的有效显示频率范围。

为了提高测量精度，示波器在设置参数的需要尽可能满足：

• 设置示波器通道增益，尽可能使得信号波形达到屏幕满幅值，这样可以最大利用示波器采样8bit的精度；
• 设置示波器时基，使得能够采样到7个周期左右的数据；
• 示波器的采样模式使用“高分辨率”采样模式；

在处理数据时，建议使用增加Hanning窗口，来减少对数据截断所带来的幅值波动。