Stanford University《Machine Learning》学习笔记(5)- 多变量线性回归
单变量线性回归
- 1 多维特征
- 2 多变量梯度下降
- 3 梯度下降法实践1 - 特征缩放
- 4 梯度下降法实践2 - 学习率
- 5 特征和多项式回归
- 6 正规方程
本次课程(共6小节)视频链接:
https://pan.baidu.com/s/1MilLGpRkhv7N311G7_vD9Q
提取码:9nnr
1 多维特征
目前为止,我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为
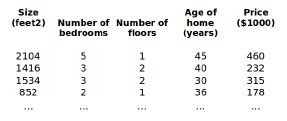
增添更多特征后,我们引入一系列新的注释:n 代表特征的数量
x i x^i xi 代表第 i i i 个训练实例,是特征矩阵中的第 i i i 行,是一个向量 ( V e c t o r ) (Vector) (Vector)。
比方说,上图的 x 2 = [ 1416 3 2 40 ] x^2 = \left[ \begin{array}{l} 1416 \\ 3 \\ 2 \\ 40 \\ \end{array} \right] x2=⎣⎢⎢⎡14163240⎦⎥⎥⎤ , x j ( i ) x^{(i)}_{^j } xj(i) 代表特征矩阵中第 i i i 行的第 j j j 个特征,也就是第 i i i 个训练实例的第 j j j 个特征。
如上图的 x 2 ( 2 ) x^{(2)}_{2} x2(2)=3, x 3 ( 2 ) x^{(2)}_{3} x3(2)=2,支持多变量的假设 h h h 表示为: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta (x) = \theta _0 + \theta _1 x_1 + \theta _2 x_2 + \cdots + \theta _n x_n hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
这个公式中有 n + 1 n+1 n+1 个参数和 n n n 个变量,为了使得公式能够简化一些,引入 x 0 x_{0} x0 = 1,则公式转化为:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta (x) = \theta _0 + \theta _1 x_1 + \theta _2 x_2 + \cdots + \theta _n x_n hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
此时模型中的参数是一个 n + 1 n+1 n+1 维的向量,任何一个训练实例也都是 n + 1 n+1 n+1 维的向量,特征矩阵 X X X 的维度是 m × ( n + 1 ) m \times (n + 1) m×(n+1)。因此
公式可以简化为: h θ ( x ) = θ T X h_\theta (x) = \theta^{T}X hθ(x)=θTX,
其中上标 T T T 代表矩阵转置。
2 多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
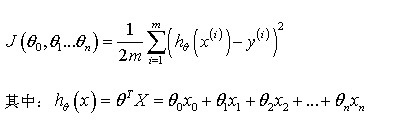
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为:


我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新值,如此循环知道收敛。
Python代码示例:
3 梯度下降法实践1 - 特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000 平方英尺,而房间数量的值则是0-5,以两个参数
分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到1 之间。如图

最简单的方法是令

4 梯度下降法实践2 - 学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何
时趋于收敛。

也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值(例如 0.001)进行比较,但通常看上面这样的图表更好。
梯度下降算法的每次迭代受到学习率的影响,如果学习率α 过小,则达到收敛所需的迭代次数会非常高;如果学习率α 过大,每次迭代可能
不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率:
α=0.01,0.03,0.1,0.3,1,3,10
5 特征和多项式回归
如房价预测问题:

x 1 x_{1} x1 = frontage(临街宽度), x 2 x_{2} x2 = depth(纵向深度), x x x = frontage*depth = area (面积),则: h θ ( x ) = θ 0 + θ 1 x 1 h_\theta (x) = \theta _0 + \theta _1 x_1 hθ(x)=θ0+θ1x1。
线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方模型: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 h_\theta (x) = \theta _0 + \theta _1 x_1 + \theta _2 x_2^2 hθ(x)=θ0+θ1x1+θ2x22
或者三次方模型: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 h_\theta (x) = \theta _0 + \theta _1 x_1 + \theta _2 x_2^2 + \theta _3 x_3^3 hθ(x)=θ0+θ1x1+θ2x22+θ3x33

通常我们需要先观察数据然后再决定准备尝试怎样的模型。另外,我们可以令:
x 2 = x 2 2 x_2 = x_2^2 x2=x22, x 3 = x 3 3 x_3 = x_3^3 x3=x33
从而将模型转化为线性回归模型。
根据函数图形特征,我们还可以使:

或者:

注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
6 正规方程
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案,如:

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:
∂ ∂ θ j J ( θ j ) = 0 \frac{\partial }{{\partial\theta _j }}J(\theta _j ) = 0 ∂θj∂J(θj)=0
假设我们的训练集特征矩阵为 X X X (包含了 x 0 x_0 x0 = 1)并且我们的训练集结果为向量 y y y,则利用正规方程解出向量 θ = ( X T X ) − 1 X T y \theta = (X^T X)^{ - 1} X^T y θ=(XTX)−1XTy。
其中上标 T T T 代表矩阵转置,上标 -1 代表矩阵的逆。设矩阵 A = X T X A = X^TX A=XTX,则: X T X = A − 1 X^TX = A^{-1} XTX=A−1
以下表示数据为例:

即:

运用正规方程方法求解参数:
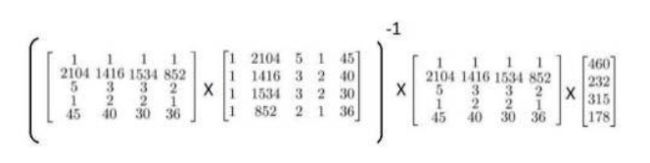
在Octavve中,正规方程写作: p i n v ( X ′ ∗ X ) ∗ X ′ ∗ y pinv(X'*X)*X'*y pinv(X′∗X)∗X′∗y
注:对于那些不可逆的矩阵(通常是因为特征之间不独立,如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征,也有可能是特征数量
大于训练集的数量),正规方程方法是不能用的。
梯度下降与正规方程的比较:
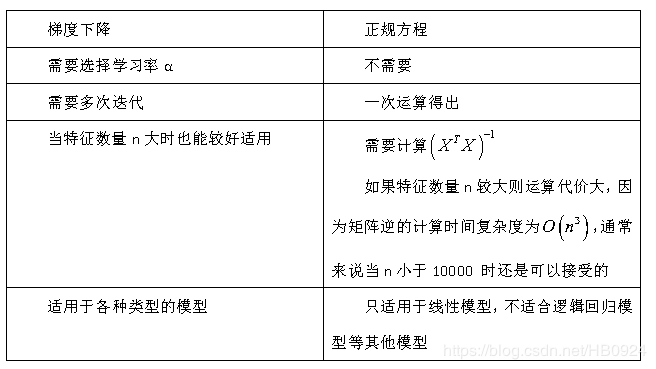
总结一下,只要特征变量的数目并不大,标准方程是一个很好计算参数 θ \theta θ的替代方法。具体地说,只要特征数量小于一万,我通常使
用标准方程法,而不使用梯度下降算法。
随着我们要讲的学习算法越来越复杂,例如,当我们讲到分类算法,像逻辑回归算法,我们会看到,实际上对于那些算法,并不能使用标准
方程法,对于那些更复杂的学习算法,我们将不得不仍然使用梯度下降法。因此梯度下降法是一个非常有用的算法,可以用在有大量特征变
量的线性回归问题上。或者我们以后会讲到一些其他的算法,因为标准方程不适合或者不能用在他们身上,但对于这个特定的线性回归模
型,标准方程是一个比梯度下降更快的替代算法。所以,根据具体的问题,以及你的特征变量的数量,这两种算法都是值得学习的。

