常见的五类排序算法图解和实现（归并类：二路归并排序）

归并类的排序算法

归并：将两个或两个以上的有序表组合成一个新的有序表。

内部排序中，通常采用的是 2-路归并排序。即：将两个位置相邻的记录有序子序列归并为一个记录有序的序列。归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

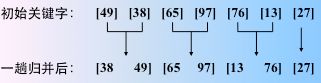
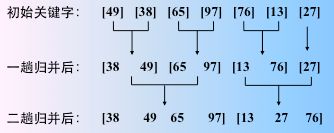
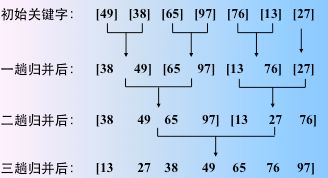
图解如下

看成是 n 个有序的子序列（长度为 1），然后两两归并。

得到 n/2 个长度为2 或 1 的有序子序列。继续亮亮归并

最后一趟

代码如下：

 1 //二路一次归并过程的算法
 2 //low为本次二路归并排序的第1有序区的第1个元素，i指向第1个元素, mid为第1有序区的最后1个元素
 3 void merge(int List[], int low, int mid, int high)
 4 {
 5     //mid+1为第2有序区第1个元素，mid为第1有序区的最后1个元素
 6     //i 指向第 1 有序区的第 1 个元素
 7     int i = low;
 8     //j 指向第 2 有序区的第 1 个元素，high 为第 2 有序区的最后一个元素
 9     int j = mid + 1;
10     //temp数组暂存合并的有序序列
11     int *temp = new int[high - low + 1];
12     //设置临时数组的指示标志 k
13     int k = 0;
14     //内存分配失败
15     if(!temp){
16         cout<<"数组分配失败！";
17         exit(0);
18     }
19     //顺序选取两个有序区的较小元素，存储到t数组中，因为是递增排序
20     while(i <= mid && j <= high){
21         //较小的元素，存入temp临时数组中
22         if(List[i] <= List[j]){
23             temp[k++] = List[i++];
24         }else{
25             temp[k++] = List[j++];
26         }
27     }// end of while
28     //比完之后，假如第1个有序区仍有剩余，则直接全部复制到 temp 数组
29     while(i <= mid){
30         temp[k++] = List[i++];
31     }
32     //比完之后，假如第2个有序区还有剩余，则直接全部复制到 temp 数组
33     while(j <= high){
34         temp[k++] = List[j++];
35     }
36     //将排好序的序列，重存回到 list 中 low 到 high 区间
37     for(i = low, k = 0; i <= high; i++, k++){
38         List[i] = temp[k];
39     }
40     //delete [] 删除动态数组的内存
41     delete []temp;
42 }
43 
44 //递归实现二路归并排序（也就是分治法的思想）
45 void mergeSort(int List[], int low, int high)
46 {
47     //二路归并排序，分为二路
48     int mid = (low + high) / 2;
49     //终止条件，low >= high， 不是while，且不含等号，否则死循环
50     if(low < high)
51     {
52         //递归过程，二路归并排序递归过程
53         mergeSort(List, low, mid);
54         mergeSort(List, mid + 1, high);
55         //归并
56         merge(List, low, mid, high);
57     }
58 }
59 
60 int main(void)
61 {
62     int source[7] = {49, 38, 65, 97, 76, 13, 27};
63     
64     mergeSort(source, 0, 6);
65     
66     for (int i = 0; i < 7; i++) {
67         printf(" %d  ", source[i]);
68     }
69     
70     return 0;
71 }

上述代码使用的是递归的方式，递归函数里，递归语句之前的语句和各级被调的递归函数执行顺序一致，而递归语句之后的语句和被调的递归函数执行顺序相反。这就是为什么 merge 函数要放在递归语句（两条递归语句）之后，因为是逆向执行的。联系二路归并排序的过程！！

还可以使用非递归的方式，代码如下：

 1 //非递归算法实现二路归并排序，length代表数组长度，即数组最大下标是 legth - 1
 2 void mergeSort(int List[],int length)
 3 {
 4     //回忆图解的过程，二路归并算法的流程，不同于递归，递归是先递归语句，然后归并函数，这样归并函数是倒序执行（和递归函数执行顺序相反）
 5     int size = 1;
 6     int low;
 7     int mid;
 8     int high;
 9     //size 是标记当前各个归并序列的high-low，从1，2，4，8，……，2*size
10     while(size <= length - 1)
11     {
12         //从第一个元素开始扫描，low代表第一个分割的序列的第一个元素
13         low = 0;
14         //当前的归并算法结束的条件
15         while(low + size <= length - 1)
16         {
17             //mid代表第一个分割的序列的最后一个元素
18             mid = low + size - 1;
19             //high 代表第二个分割的序列的最后一个元素
20             high = mid + size;
21             //判断一下：如果第二个序列个数不足size个
22             if(high > length - 1){
23                 //调整 high 为最后一个元素的下标即可
24                 high = length - 1;
25             }
26             //调用归并函数，进行分割的序列的分段排序
27             merge(List, low, mid, high);
28             //打印出每次归并的区间
29             cout << "low:" << low << " mid:" << mid << " high:" << high << endl;
30             //下一次归并时第一序列的第一个元素位置
31             low = high + 1;
32         }// end of while
33         //范围扩大一倍，二路归并的过程
34         size *= 2;
35     }// end of while
36 }

二路归并排序算法分析

每趟归并的时间复杂度为O(n)，共需进行 log2 n 趟。

二路归并排序的时间复杂度：等于归并趟数与每一趟时间复杂度的乘积。时间复杂度为O(nlog2n)。

利用二路归并排序时，需要利用与待排序数组相同的辅助数组作临时单元，故该排序方法的空间复杂度为O(n)，比前面介绍的其它排序方法占用的空间大。

由于二路归并排序中，每两个有序表合并成一个有序表时，若分别在两个有序表中出现有相同排序码，则会使前一个有序表中相同排序码先复制，后一有序表中相同排序码后复制，从而保持它们的相对次序不会改变。所以，二路归并排序是一种稳定的排序方法。

归并的思想主要用于外部排序：

外部排序可分两步

①待排序记录分批读入内存，用某种方法在内存排序，组成有序的子文件，再按某种策略存入外存。

②子文件多路归并，成为较长有序子文件，再记入外存，如此反复，直到整个待排序文件有序。

外部排序可使用外存、磁带、磁盘，最初形成有序子文件长取决于内存所能提供排序区大小和最初排序策略，归并路数取决于所能提供排序的外部设备数。

 

转载于:https://www.cnblogs.com/kubixuesheng/p/4355865.html