一些平面几何证明题

背景

搜集了好几个平面几何问题。特征是，辅助线类似的线索。找不到线索一筹莫展。线索找到之后，所用的数学知识相对简单。

问题之一

连续使用相似三角形也可以证明。初中练习题。——有时候，解初中小学问题，因为知识面的原因，了解的太多、想得太多，思路反而更发散，无形中提高了解决问题的难度。

如图， O 是 ΔABC 内一点； CF 、 BE 交于 O ， EF//BC ；
求证： BD=CD 。

证明：

然而如果知道塞瓦定理，证明也很方便。

塞瓦定理的证明其实简单，但是能够作为一个著名定理而把一个人名流传下来，必然有它的不一般之处，能够在考场上临战状态下得到这样的结果，相当于隔空秒杀了一位古人。

这个定理的结果，用在这里就是，

BDDC⋅CEEA⋅AFFB=1(0)

证明这个式子可以利用三角形面积的比值：
BDDC=SΔABDSΔADC=SΔOBDSΔODC=SΔABD−SΔOBDSΔADC−SΔODC=SΔABOSΔAOC
类似有：

CEEA=SΔBCOSΔABO,AFFB=SΔAOCSΔBCO(0.1)

它们相乘就是塞瓦定理的结果了：

BDDC⋅CEEA⋅AFFB=SΔABOSΔAOC⋅SΔBCOSΔABO⋅SΔAOCSΔBCO=1(0.2)

这个结果，加上由 EF//BC 得到的：

AFFB=EACE⇒AFFB⋅CEEA=1⇒BDDC=1

也就是要证明的结论。

这个问题其实可以有更简单的证明。
假设 EF∩AD=G

利用平行关系，可以把相思从左传递到右，从上传递到下。

EGBD=OGOD=FGCD

⇒EG+FGBD+CD=OGOD=EFBC

∵EFBC=AGAD=EGCD=FGBD

∴EGCD=AGAD=EFBC=OGOD=EGBD

EGBD=AGAD=EFBC=OGOD=FGCD

都能得到

BD=CD

。

用塞瓦定理算误入歧途呢，还是知道得太多反而思维更容易发散、反而无形中倾向于高难度的解法？

问题之1.1

这里是临时找一个似乎不太容易避开塞瓦定理的，
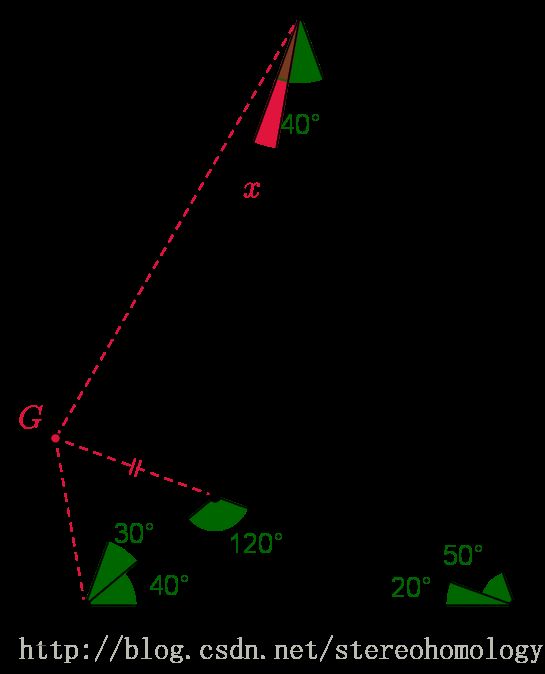
已知，如图， AB=AC , ∠BAC=40° ， D 在三角形内， ∠CBD=40°，∠BCD=20° 。

求证： AD=CD+BD

作辅助线如图红色部分， G 在 CD 延长线上， DG=BD ；如果能够证明 x=∠BAD=10° ， 后面只须，先证明 ΔBDG 是等边三角形，以及 ΔABD≅ΔABG ，

则 ∠CAG=50°⇒AG=CG⇒AD=CD+BD .

参加竞赛的同学都叫角元塞瓦定理，在上图中就是：

sin∠ABDsin∠DBC⋅sin∠BCDsin∠DCA⋅sin∠CADsin∠DAB=1

假设了 ∠DAB=x ， 则上式变为：

sin∠30°sin∠40°⋅sin∠20°sin∠50°⋅sin∠(40°−x)sinx=1

以及如何由此证明 x=10° ；暂时看不到其它简单的方法。可能又要用到恐怕只有竞赛前的训练才可能涉及到的一些三角函数变换技巧了。竞赛难度主要体现在，需要使用一些有难度的、延伸性的结果（或竞赛专用知识点）作为起点，有了这些起点作为基础，更进一步似乎难度也是常规性质的。

问题之二

ΔABC 中， BD=CE ， ∠1+∠2=∠3+∠4 。 求证： AB=AC

没想到网友用了个极其简单的方法，反证法就证明了。因为本来的原始问题，被称为 Steiner-Lehmus 问题 ，也是有一定难度的。

没想到作如图辅助线，反证法就能解决。 作 EG//BD ， DG//BE ，得到平行四边形 BDGE

则： CE=BD=EG⇒∡1+∠6=∠3+∠5

如果
∠3>∠1⇒∠5<∠6(1)

又 ∵∠1+∠2=∠3+∠4

同上假设：

∠3>∠1⇒∠4<∠2⇒CD<BE⇒CD<DG⇒∠6<∠5(2)

(1)和 (2) 矛盾。类似地， 如果假设 ∠3<∠1 ， 从两个途径推导的 ∠5 和 ∠6 的关系也矛盾。

这样就只能 ∠1=∠3 ， 从而 ∠2=∠4 ， ∠5=∠6

从而 ∠1+∠4=∠3+∠2 得到等腰三角形。 ——基本上没有用到特别高级的知识， 但是如果强行从证明回答这个问题证明，难度瞬间提升。

问题之三

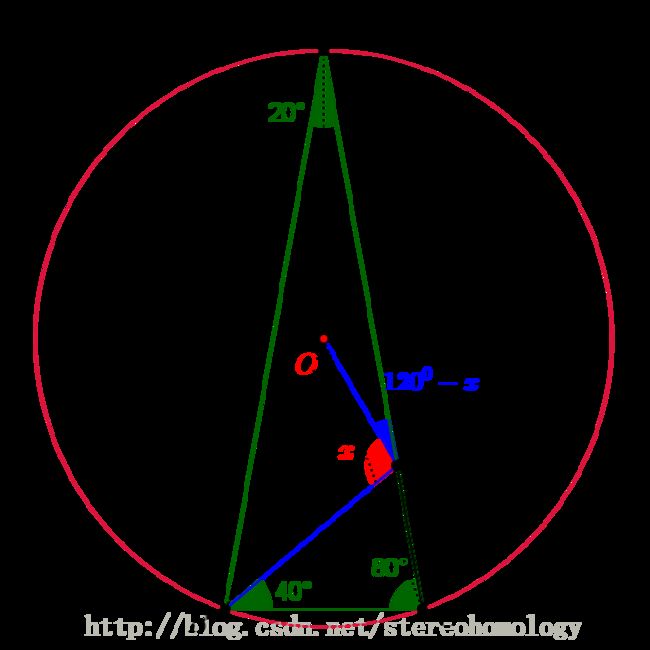
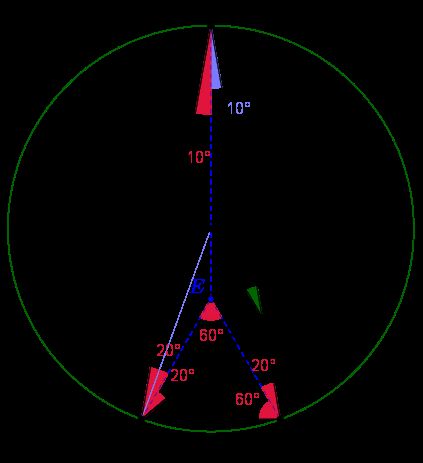
已知如上图 AB=AC , ∠BAC=20° ， O 是外接圆圆心， BD 平分 ∠ABC ，几何方法求 x 的角度。

代数方法求得的关系式化简的难度极高，所以并不理想。这道题跟世上最难的初等几何问题简直用的是同一个图。我一直以为难度不低，但是没想到，找对了正确的几何的方法作辅助线，可以简单化到这种程度。下面是辅助线作法。

过两个底边顶点，作跟底边呈60°的射线如图，相交于 E ，则该点在底边的中垂线上，也就是直线 AO 上，因为 O 是外接圆圆心。连 BO

从角度标记容易发现，

1. BO 是 ∠ABC 的角平分线 ⇒ΔABE 中， ABBE=AOOE
2. BD 是 ∠ABC 的角平分线 ⇒ΔABC 中， ABBC=ADDC

等边三角形 ΔBCE 中 BE=BC ，所以：

AOOE=ABBE=ABBC=ADDC⇒OD//EC

∴∠ADO=∠ACE=20°

因为 ∠ADB=120°，x=∠ADB=∠ADO=100°

总结

这里的问题，尤其后面两道，代数方法可以做，但是非常繁琐。几何方法不容易想到（发散），但是一旦找对方法，问题简单得不可思议。

第一道题，我初中的时候做应该不至于被带歪到塞瓦定理这样的歧途上去。对了，塞瓦定理居然还有角元版本，这个更是在有些问题的证明中有妙用。

所以，知道的知识或方法更多，对求解初等数学问题来说，尤其是这类平面几何的，从找最简单优美解法的角度，未必是一种优势。因为思路更加发散了。——求解初等问题，最不习惯的一个约束是，常常要问自己，这个知识点是不是初等数学范畴的？