pytorch的基本使用, 函数实现SDG法训练网络, 梯度下降法(DG)案例
1 pytorch的概念
1.1 tensor张量
1.1.1 PyTorch的tensor与NumPy array相互转换
PyTorch的很多操作和numpy都是类似的,但是因为其能够在 GPU 上运行,所以比 NumPy 快很多。
import torch
import numpy as np
# 创建一个 numpy ndarray
numpy_tensor = np.random.randn(10, 20)
x = torch.randn(10, 20)
1.1.1.1 ndarray==>tensor
- torch.Tensor 强制类型转换
- torch.from_numpy创建函数
pytorch_tensor1 = torch.Tensor(numpy_tensor)
pytorch_tensor2 = torch.from_numpy(numpy_tensor)
print(type(pytorch_tensor2))
print(type(pytorch_tensor1))
1.1.1.2 tensor==>ndarray
# 如果 pytorch tensor 在 cpu 上
numpy_array = pytorch_tensor1.numpy()
# 如果 pytorch tensor 在 gpu 上
numpy_array = pytorch_tensor1.cpu().numpy()
1.1.2 PyTorch Tensor 使用 GPU 加速
# 第一种方式是定义 cuda 数据类型
dtype = torch.cuda.FloatTensor # 定义默认 GPU 的 数据类型
gpu_tensor = torch.randn(10, 20).type(dtype)
# 第二种方式更简单,推荐使用
gpu_tensor = torch.randn(10, 20).cuda() # 将 tensor 放在GPU 上
1.1.3 tensor的属性
# 可以通过下面两种方式得到 tensor 的大小
print(pytorch_tensor1.shape)
print(pytorch_tensor1.size())
# 得到 tensor 的数据类型
print(pytorch_tensor1.type())
## 维度
print(pytorch_tensor1.dim())
# 得到 tensor 的所有元素个数
print(pytorch_tensor1.numel())
1.1.4 tensor的数据类型变换
x = torch.randn(3, 2)
print(x)
x = x.type(torch.DoubleTensor)
print(x)
x_array = x.numpy()
print(x_array.dtype)
1.2 tensor的操作
1.2.1 squeeze和unsqueeze操作: 降维升维
print(torch.ones(2, 2))
#torch.Size([2, 2])
print(torch.ones(2, 2).size())
x = torch.ones(2, 2).unsqueeze(0)
torch.Size([1, 2, 2])
print(x)
print(x.size())
# 将 tensor 中所有的一维全部都去掉
x = x.squeeze()
print(x)
print(x.shape)
1.2.2 数值类型转换
# 将其转化为整形
x = x.long()
# x = x.type(torch.LongTensor)
print(x.type())
1.2.3 使用permute和transpose进行维度交换
x = torch.randn(3, 4, 5)
print(x.shape)
# 使用permute和transpose进行维度交换
x = x.permute(1, 0, 2) # permute 可以重新排列 tensor 的维度
print(x.shape)
x = x.transpose(0, 2) # transpose 交换 tensor 中的两个维度
print(x.shape)
1.2.4 使用 view 对 tensor 进行 reshape
x = torch.randn(3, 4, 5)
print(x.shape)
## 拉伸
x = x.view(-1, 5) # -1 表示任意的大小,5 表示第二维变成 5
print(x.shape)
x = x.view(3, 20) # 重新 reshape 成 (3, 20) 的大小
print(x.shape)
1.2.5 tensor的运算:相加
x = torch.zeros(3, 4)
y = torch.ones(3, 4)
# 两个 tensor 求和
z = x + y
print(z)
z = torch.add(x, y)
print(z)
1.2.6 tensor的inplace操作
pytorch中大多数的操作都支持 inplace 操作,也就是可以直接对 tensor 进行操作而不需要另外开辟内存空间。方式非常简单,一般都是在操作的符号后面加_
1.3 变量
- from torch.autograd import Variable
- Variable 是对 tensor 的封装,操作和 tensor 是一样的,
- 但是每个 Variabel都有三个属性,Variable 中的
.data,梯度.grad以及这个 Variable 是通过什么方式得到的.grad_fn。
1.3.1 变量的梯度
# 通过下面这种方式导入 Variable
from torch.autograd import Variable
x_tensor = torch.randn(10, 5)
y_tensor = torch.randn(10, 5)
# 将 tensor 变成 Variable
# 默认 Variable 是不需要求梯度的,所以我们用这个方式申明需要对其进行求梯度
x = Variable(x_tensor, requires_grad=True)
2 梯度下降法Gradient Descent (GD)介绍
2.1 梯度下降法简介
2.1.1 梯度
比如一个一个函数 f ( x , y ) f(x, y) f(x,y),那么 f f f 的梯度就是
( ∂ f ∂ x , ∂ f ∂ y ) (\frac{\partial f}{\partial x},\ \frac{\partial f}{\partial y}) (∂x∂f, ∂y∂f)
可以称为 g r a d f ( x , y ) grad f(x, y) gradf(x,y) 或者 ∇ f ( x , y ) \nabla f(x, y) ∇f(x,y)。具体某一点 ( x 0 , y 0 ) (x_0,\ y_0) (x0, y0) 的梯度就是 ∇ f ( x 0 , y 0 ) \nabla f(x_0,\ y_0) ∇f(x0, y0)。
2.1.2 学习率
- 来沿着梯度的反方向,我们能够更快地找到函数的最小值点
- 我们需要每次往下走的那一步的长度,这个长度称为学习率,用 ? 表示
- 学习率太小会导致下降非常缓慢
- 学习率太大又会导致跳动非常明显
2.1.3 更新梯度公式
w i + 1 = w i − η ∂ f ( w ) ∂ w w_{i+1}= w_{i} - \eta \frac{\partial f(w)}{\partial w} wi+1=wi−η∂w∂f(w)
- 1 w i + 1 w_{i+1} wi+1是第t+1步的位置,
- 2 ∂ f ( w ) ∂ w \frac{\partial f(w)}{\partial w} ∂w∂f(w) 是微分,
- 3 η \eta η是步长
2.2 梯队下降的缺点
- 鞍点
- 一个不是局部最小值的驻点(一阶导数为0的点)称为鞍点。
- 数学含义是: 目标函数在此点上的梯度(一阶导数)值为 0, 但从改点出发的一个方向是函数的极大值点,而在另一个方向是函数的极小值点
鞍点的例子 z = x 2 − y 2 z = x^{2} - y^{2} z=x2−y2, 函数图形为
z = x 4 − y 3 z = x^{4} - y^{3} z=x4−y3 的(0,0)也是鞍点
2.3 Stochastic Gradient Descent (SGD) 算法
2.3.1 SGD的理解
- 用一张图来表示,其实SGD就像是喝醉了酒的GD,它依稀认得路,最后也能自己走回家,但是走得歪歪扭扭
- 虽然包含一定的随机性,但是从期望上来看,它是等于正确的导数的.
2.3.2 SGD的公式
w i + 1 = w i − η J w_{i+1}= w_{i} - \eta J wi+1=wi−ηJ
- w i + 1 w_{i+1} wi+1是第t+1步的位置, J J J 是随机微分, η \eta η是步长
- J J J的期望满足梯队函数
E [ J ] = ∂ f ( w ) ∂ w E[J]= \frac{\partial f(w)}{\partial w} E[J]=∂w∂f(w)
3 pytorch函数实现梯度下降法: 线性回归
3.1 线性回归的参数的误差更新公式
3.1.1 线性回归的公式:
y ^ i = w x i + b \hat{y}_i = w x_i + b y^i=wxi+b
y ^ i \hat{y}_i y^i 是我们预测的结果,希望通过 y ^ i \hat{y}_i y^i 来拟合目标 y i y_i yi,通俗来讲就是找到这个函数拟合 y i y_i yi 使得误差最小,即最小化损失函数定义为
J = 1 n ∑ i = 1 n ( y ^ i − y i ) 2 J=\frac{1}{n} \sum_{i=1}^n(\hat{y}_i - y_i)^2 J=n1i=1∑n(y^i−yi)2
3.1.2 梯队下降
J J J对 w , b w,b w,b求偏导, 微分得到 w i + 1 {w}_{i+1} wi+1 和 w i {w}_i wi的关系, b i + 1 {b}_{i+1} bi+1 和 b i {b}_i bi的关系如下
w : = w − η ∂ f ( w , b ) ∂ w b : = b − η ∂ f ( w , b ) ∂ b w := w - \eta \frac{\partial f(w,\ b)}{\partial w} \\ b := b - \eta \frac{\partial f(w,\ b)}{\partial b} w:=w−η∂w∂f(w, b)b:=b−η∂b∂f(w, b)
通过不断地迭代更新,最终我们能够找到一组最优的 w 和 b,这就是梯度下降法的原理。
3.1.3 线性回归的梯度下降
w 和 b 的梯度分别是
∂ J ∂ w = 2 n ∑ i = 1 n x i ( w x i + b − y i ) ∂ J ∂ b = 2 n ∑ i = 1 n ( w x i + b − y i ) \frac{\partial J}{\partial w} = \frac{2}{n} \sum_{i=1}^n x_i(w x_i + b - y_i) \\ \frac{\partial J}{\partial b} = \frac{2}{n} \sum_{i=1}^n (w x_i + b - y_i) ∂w∂J=n2i=1∑nxi(wxi+b−yi)∂b∂J=n2i=1∑n(wxi+b−yi)
3.2 代码实现
import torch
import numpy as np
from torch.autograd import Variable
import matplotlib.pyplot as plt
%matplotlib inline
# 定义随机因子
torch.manual_seed(2019)
3.2.1 创建张量tensor(测试样本数据)
tensor的使用接口和 numpy 非常相似
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
[9.779], [6.182], [7.59], [2.167], [7.042],
[10.791], [5.313], [7.997], [3.1]], dtype=np.float32)
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
[3.366], [2.596], [2.53], [1.221], [2.827],
[3.465], [1.65], [2.904], [1.3]], dtype=np.float32)
# 转换成 Tensor
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)
3.2.2 创建变量Variable
- from torch.autograd import Variable
- Variable 是对 tensor 的封装,操作和 tensor 是一样的,
- 但是每个 Variabel都有三个属性,Variable 中的.data,梯度.grad以及这个 Variable 是通过什么方式得到的.grad_fn
# 定义参数 w 和 b
w = Variable(torch.randn(1), requires_grad=True) # 随机初始化
b = Variable(torch.zeros(1), requires_grad=True) # 使用 0 进行初始化
x_train = Variable(x_train)
y_train = Variable(y_train)
print(w)
print(b)
tensor([-0.1187], requires_grad=True)
tensor([0.], requires_grad=True)
3.2.3 构建计算图: 拟合模型,损失函数
def linear_model(x):
return x * w + b
# 计算误差
def get_loss(y_, y):
return torch.mean((y_ - y_train) ** 2)
3.2.4 训练模型
3.2.4.1 训练模型-查看初始化参数的模型
- 目的:
- 根据初始超参数, 计算第一次估计的y值
- 根据第一次估算的值, 计算误差
- 画图
- tensor的data属性
- plt的输入为numpy类型
y_ = linear_model(x_train)
loss = get_loss(y_, y_train)
# 打印一下看看 loss 的大小
print(loss)
tensor(10.2335, grad_fn=)
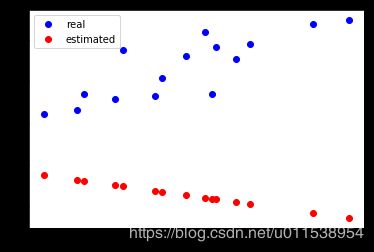
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.legend()
3.2.4.2 训练模型-第一次通过损失函数的梯队来优化参数,优化模型
注: 第一次不需要梯度归零 grad.zero_()
否则None,‘NoneType’ object has no attribute ‘zero_’
## 计算w,b梯队微分
# 将 tensor 变成 Variable
# 默认 Variable 是不需要求梯度的,所以我们用这个方式申明需要对其进行求梯度
# 根据tensor的gent_loss损失函数计算图中, x,y已知的损失值tensor对象Loss
## 自动对tensor对象求求参数的偏导函数,并且计算梯队微分
#x = Variable(x_tensor, requires_grad=True)
#y = Variable(y_tensor, requires_grad=True)
print(loss)
loss.backward()
print(w.grad)
print(b.grad)
tensor(10.2335, grad_fn=)
None
tensor([-41.1289])
tensor([-6.0890])
3.2.4.3 根据学习率和计算的w,b的梯队来更新w,b的参数
# 梯队下降,减去学习率*梯队微分, 更新一次参数
w.data = w.data - 1e-2 * w.grad.data
b.data = b.data - 1e-2 * b.grad.data
y_ = linear_model(x_train)
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.legend()
3.2.4.4 迭代30次,训练模型的参数
for e in range(31): # 进行 30 次更新
y_ = linear_model(x_train) ## 计算拟合的Y值: tensor
loss = get_loss(y_, y_train) ## 计算损失值: tensor
w.grad.zero_() # 记得归零梯度
b.grad.zero_() # 记得归零梯度
# 自动求导,计算梯队w.grad.data,b.grad.data
loss.backward()
# 使用梯队更新参数
w.data = w.data - 1e-2 * w.grad.data # 更新 w
b.data = b.data - 1e-2 * b.grad.data # 更新 b
if e%10==0:
print('epoch: {}, loss: {}'.format(e, loss.item()))
epoch: 0, loss: 0.4142104387283325
epoch: 10, loss: 0.2260516732931137
epoch: 20, loss: 0.2231873869895935
epoch: 30, loss: 0.2204667031764984
y_ = linear_model(x_train)
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.legend()
4 pytorch函数实现实现SGD: mnist手写体识别
4.1 加载数据
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
%matplotlib inline
4.1.1 数据转换规范
def transform_mnist(x):
x = np.array(x, dtype='float32') / 255 # 将数据变到 0 ~ 1 之间
x = (x - 0.5) / 0.5 # 标准化,这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x
4.1.2 从下载的文件中加载数据
def download_mnist_data(batch_size):
# transform 函数式编程, 对数据的变换 train指定测试训练
# 载入数据集,申明定义的数据变换
# 定义train=True or false
train_set = MNIST(r'E:\ai\ai_lab\ai_case\ai_data\pytorch\MNIST\data', train=True, transform=transform_mnist, download=False)
test_set = MNIST(r'E:\ai\ai_lab\ai_case\ai_data\pytorch\MNIST\data', train=False, transform=transform_mnist, download=False)
# 加载数据,打乱数据
## DataLoader: 批量取多少图片
train_data = DataLoader(train_set, batch_size=batch_size, shuffle=True)
return train_data
4.2 定义网络结构,定义损失函数,定义SDG函数
4.2.1 使用 Sequential 定义 3 层神经网络
# 最后一层10个输出
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
4.2.2 定义损失函数
# 交叉熵函数
criterion = nn.CrossEntropyLoss()
4.2.3 定义SDG函数
def sgd_update(parameters, lr):
for param in parameters:
param.data = param.data - lr * param.grad.data
4.3 训练网络
4.3.1 定义网络训练的函数过程
注1: 梯队归零的方法
- 直接把模型的参数梯度设成0:
- model.zero_grad()
- optimizer.zero_grad()
- 当optimizer=optim.Optimizer(model.parameters())时,两者等效
- 如果想要把某一Variable的梯度置为0
- Variable.grad.data.zero_()
def train_net(net,train_data,lr):
train_losses=[]
train_loss = 0
losses_idx = 0
### batch_size影响im,label的大小
### batch_size影响迭代次数.
for im, label in train_data:
# 定义变量:
im = Variable(im)
label = Variable(label)
# 前向传播,传入输入tensor,获得输出tensor
out = net(im)
# 计算损失tensor: 根据前向传播的预测值和真是标签
loss = criterion(out, label)
# 将网络的所有参数的梯度属性置为零
net.zero_grad()
# 默认 Variable 是不需要求梯度的, requires_grad=True 这个方式申明需要对其进行求梯度
# 损失值tensor的对网络参数的偏导
loss.backward()
## 对模型参数更新,
## 属性 net.parameters得到所有参数
sgd_update(net.parameters(),lr) # 使用lr的学习率
# 记录误差
train_loss += loss.item()
if losses_idx % 10 == 0:
train_losses.append(loss.item())
losses_idx += 1
return (train_losses,train_loss,losses_idx)
4.3.2 定义主函数
def train(net,train_data,lr,batch_size):
start = time.time() # 记时开始
# 训练网络,记录损失值
(train_losses,train_loss,losses_idx)=train_net(net,train_data,lr)
end = time.time() # 计时结束
print('epoch: 1, Train Loss: {:.6f}'.format(train_loss / len(train_data)))
print('使用时间: {:.5f} s'.format(end - start))
x_axis = np.linspace(0, 5, len(train_losses), endpoint=True)
plt.semilogy(x_axis, train_losses, label='batch_size=%d'%batch_size)
plt.legend(loc='best')
4.3.3 开始训练网络
定义学习率和批量规模
batch_size=100
lr=1e-2
下载数据, 使用torch.utils.data.DataLoader方法批量加载数据
train_data=download_mnist_data(batch_size=batch_size)
训练数据, 根据批量规模, 训练所有的数据
train(net,train_data,lr=1e-2,batch_size=100)
epoch: 1, Train Loss: 0.905261
使用时间: 7.80006 s