动手学习深度学习——卷积神经网络基础

  这个系列确实不太好写，训练网络准备数据等等都需要花费不少时间，所以更新会比较慢一些，orz。
  本博客的主要内容还是偏向于卷积神经网络(CNN)，至于其他种类的深度学习，这里暂不涉及。如果觉得有用，可以顺手点个赞，也欢迎在留言板讨论交流，文中如有错误，请指出说明，谢谢。

1. 深度学习基本网络层

1.1 卷积层

  1). 卷积层的工作原理
  卷积计算的过程如下图所示，灰色的代表图像，每个格子代表一个像素点，橙色的是卷积核。卷积核在图像中移动，卷积核上1-9的位置都有对应的系数，每个系数都乘以对应图像位置的数值(如1’-9’)，然后相加后作为结果，存在卷积核中心对应的图像位置(如图中的5’)。然后根据设定好的步长 $s$ ，卷积核向右移动 s 个像素(如图为步长为1的时候卷积核移动的结果)，如果超出图像范围就换行从头开始。
  什么叫边缘填充(padding)呢？简单来说就是在卷积前对原始图像的周围进行填0或其他数值(如下图的绿色区域)。通过适当的填充，可以让图像在卷积后的尺寸保持不变，这时进行边缘填充最常见的目的。
    

  在深度学习里，常说的卷积层输入通道和输出通道又是什么意思呢？众所周知，通常彩色图像都不是简单的$m\times n$的二维数据，而是$m\times n\times 3$的三维数据，图像中也成为3通道，每个$m\times n\times 1$分别代表R、G、B颜色通道，如果把这样的三维数据输入卷积层，就称卷积层的输入是3通道的(input_channels=3)。
  这时，假设卷积层卷积核的尺寸为$3\times 3$，系数也初始化设定好了，要怎么对三维数据进行卷积呢？很简单，也把卷积核扩充为三维的，且通道数和卷积层的输入通道数相同，也就是$3\times 3\times 3$。其中，3个$3\times 3\times 1$模块的系数是一模一样的，相当于将原来的$3\times 3$卷积核沿第三个维度复制了三份。这时候，再对图像进行和2维卷积一样的操作，$3\times 3\times 3$卷积核每个位置的系数乘上对应位置的数据，并全部相加，就计算得到卷积核中心位置的数值结果。细心的读者可能发现了，这么做之后，原来输入的$m\times n\times k$维的数据，就变成了$m^{\prime }\times n^{\prime }\times 1$，也就是多通道的数据变成了单通道了。用深度学习的术语来说，就是数据输入卷积层后，经过一个卷积核卷积，就生成一个特征图(feature map)。那么，如果有$k^{\prime }$个不同的卷积核，就能生成$k^{\prime }$个feature map，把所有的feature map累加起来，就形成了卷积层的输出$m^{\prime }\times n^{\prime }\times k^{\prime }$。所以，就把输入数据的通道数$k$称为卷积层的输入通道数，卷积核的个数$k^{\prime }$称为输出通道数。

  因此，对于卷积层来说，最重要的参数有

• 输入通道数 input_channels
• 输出通道数 output_channels
• 卷积核尺寸 k (通常是奇数且是正方形)
• 步长 s
• 边界填充 p (padding)

  要说明的一点是，深度学习中所提到的卷积操作，其实严格来说不是卷积，而是相关操作。卷积和相关的唯一区别就是，卷积核是相关核旋转180°后得到的(详情参见“数字图像处理——灰度变换、直方图、卷积介绍及空间滤波器”中的卷积介绍)。但其实深度学习中，使用卷积操作还是用相关操作，影响是不大的，因为深度学习中卷积核的系数都是通过学习得到的，无论你用卷积操作还是用相关操作，学习得到的系数只是旋转了180°，没有本质区别，因此为了方便计算，使用相关操作。

  2). 卷积层的输入输出尺寸计算
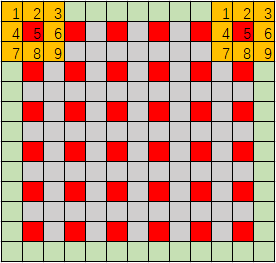
  刚刚描述了卷积层输入数据变成输出数据的过程，那么具体输入输出数据的尺寸和卷积核尺寸有什么关系呢？下图就进行了很好的说明，图中输入数据尺寸为$11\times 11$(忽略通道数)，图中红色像素表示卷积核滑过整张图像时，卷积核中心会经过的位置，其实拼接起来就是输出数据的feature map，也就是$6\times 6$。由图可知，卷积层使用的$k=3,s=2,p=1$。所以，尺寸计算公式如下：
$$outputsize=\frac{inputsize+2p-k}{s}+1$$

  3). 大尺寸卷积核与小尺寸卷积核的优缺点
  直观而言，有两个明显的差异:

• 相比于小尺寸卷积核，大尺寸卷积核的系数多，所需的训练参数也就多，训练起来也就更慢；
• 相比于小尺寸卷积核，大尺寸卷积核对原图像的覆盖面更广，卷积操作提取的特征本身就是区域特征，因此大卷积核提取的特征对应的区域也就大，如下图橙色和蓝色的区域大小比较。这种feature map映射到原始图像的覆盖范围，就称为感受野(receptive field)
  

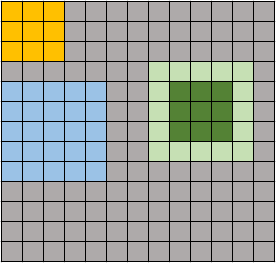
  但是，VGG的论文中提到，其实可以用两层卷积核为$3\times 3$的卷积层来代替一层卷积核为$5\times 5$的卷积层，因为它们俩的感受野是一样的。如上图绿色区域，第一个$3\times 3$的卷积层在对浅绿色($5\times 5$)区域卷积后，得到$3\times 3$的feature map(深绿色)，然后该区域再经过第二个$3\times 3$的卷积层后，就得到一个特征，该特征映射到原图像中的感受野就是浅绿色$5\times 5$的区域。可以看到，这与直接用一层$5\times 5$的卷积层的感受野是相同的。不仅如此，两个$3\times 3$卷积层的参数个数(忽略通道数)为$3\times 3\times 2=18$，相比于一个$5\times 5$卷积层的参数个数$5\times 5\times 1=25$还要少，因此深度学习中经常用多层小卷积核来代替单层大卷积核。

1.2 1x1卷积层

  1). 1x1卷积层的含义和作用
  1x1卷积层看起来好像只对输入数据进行了等比例的数据缩放，对于单通道情况确实如此。但是输入数据是多通道的，使用1x1卷积层，相当于将输入数据相同位置不同通道的特征进行加权整合。另外，如果使用多个1x1卷积层，还可以将输入数据的通道数进行升维或降维操作。

  2). 1x1卷积层的实际应用(GoogLeNet,ResNet中的应用差别)
  这里对论文不展开，后续博客会具体介绍各个CNN网络。
  简单介绍一下，在GoogLeNet的Inception模块中，由于使用了多条线路并行，最后将并行结果按数据通道方向叠加的操作，如果不对输入数据的通道数进行降维，那么会导致后续卷积层的输入通道数很大，从而导致网络参数过多。因此，在Inception模块中(参见2.2节)，每条并行路线上都增加了1×1卷积层，目的就是为了对数据降维，防止输入卷积层的通道数过大。
  而在ResNet中，由于采用短路(short cut)连接，如果被短路部分的卷积层进行了通道数增加的操作，那么短路连接将两部分叠加的时候，会因为通道数不同而无法叠加。因此，通常在短路线路上会增加1×1卷积层，进行升维(因为通常网络越深，数据通道数是增加的，所以是升维)。

1.3 池化层

  1).池化层的作用
  池化层通常的目的是为了缩小数据尺寸，将一定范围内的重要信息进行整合和过滤，使池化层输出的数据相对于输入数据来说具有更高的信息密度。因此，池化层通常采用的步长和卷积核尺寸是一样的，这有助于缩小数据尺寸。
  当然，在AlexNet中，也出现了步长小于卷积核尺寸的情况，这称为重叠池化(Overlap pooling)。和非重叠池化相比，重叠池化保留的信息量更大，但相对的网络参数也就会更多。
  2). 最大池化层
  最大池化层的操作就是，对卷积核覆盖的区域，取其最大值作为卷积结果。最大池化的作用可以理解为，在一定范围内保留最强的特征，过滤掉次要特征。
  3). 平均池化层
  平均池化层的操作就是，对卷积核覆盖的区域，取其均值作为卷积结果。平均池化的作用可以理解为，将一定范围内的区域特征进行整合。
  4). 全局平均池化层(GVP)及其应用
  全局平均池化层是使用一个和数据尺寸一模一样大小的卷积核进行平均池化操作，也就是，对一整个通道的feature map进行取均值操作，变成单像素的feature map。所以，全局平均池化层的输出就是尺寸为1×1的多通道数据。因此，GVP的主要作用是可以用卷积操作来替代全连接层，同时还可以减少全连接层产生的大量的网络参数。

1.4 激活层

  其实就是之前提到的激活函数，用来增加网络的非线性能力(non-linearity)，常见的有：sigmoid,ReLU,tanh,RReLU,Leaky ReLU等等。

1.5 Batchnorm层(BN层)

  1). BN层的原理
  2). BN层的作用及其在训练和预测时的状态不同点
  3). BN层放置的位置

1.6 Dropout层

  1). dropout层的原理
  dropout就是在网络层与层之间各个神经元连接的时候，增加一个概率p，使得当前训练情况下，有概率p将其对应的连接线路舍弃。因此，在每批数据训练的时候，大体网络结构是相同的，但是有dropout层的层与层之间的神经元连接是有略微不同的，有时候有些连接会启用，有时候会被舍弃。这就使得其实训练每批数据的网络都是总体网络的子网络，且每次的子网络都不大一样。
  这样的好处是，直观上可以减少网络的复杂度(参数)。防止网络的过拟合情况。

  2). dropout层的作用及其在训练和预测时的状态不同
  根据dropout的原理可知，在训练时会按一定概率删除一定量的连接路线。那么在网络训练完成后，进行数据预测时，dropout的工作情况是怎么样的？其实在网络训练完成后，dropout层就完成任务了，在进行预测工作时，并不进行dropout操作，因此，相当于dropout层是使得在训练时使用不同的子网络进行训练，子网络相同网络层的参数都共享。然后在预测时，将所有子网络整合为总网络进行预测。所以，增加了dropout层，有点像是机器学习中的提升方法，从而提高网络的效果，还能防止网络的过拟合。

1.7 空洞卷积(AtrousConvolution)

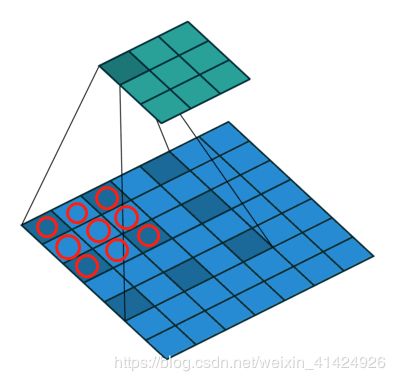
  空洞卷积正如其名，就是在普通卷积的基础上，增加空洞(dilation)。如上图所示，普通卷积操作是作用在9个相邻的方格上(红圈)，此时可以认为是dilation=1的空洞卷积，也就是每个方格相隔一个方格。而空洞卷积，同样是作用在9个方格，但是却不再相邻，上图的深蓝色区域是dilation=2的空洞卷积，每个有效方块之间间隔两个方格。
  空洞卷积最大的作用其实也很直观，就是在不增加参数的情况下，扩大卷积层的感受野。设置不同的dilation rate，可以拥有不同感受野的卷积层，利用这种方式，有学者提出了ASPP(Atrous Spatial Pyrimaid Pooling)的池化结构。
  另外，空洞卷积的输入输出尺寸也和普通卷积有所不同。可以看出，一个卷积核为$k\times k,dilation=d$的空洞卷积，其实相当于卷积核为$[k+(k-1)(d-1)]\times [k+(k-1)(d-1)]$普通卷积，因此，其输入输出尺寸的计算如下：
$$outputsize=\frac{inputsize+2p-[k+(k-1)(r-1)]}{s}+1$$
  当然，空洞卷积也有很明显的问题：

• 虽然扩大了感受野，但是其作用的有效区域并不是连续的，这对图像分类任务来说或许影响不大，但是如果是像素级的图像分割任务，那么是非常致命的。
• 当dilation的数值较大时，空洞卷积可能会忽略小目标物体的特征，因此在使用空洞卷积时，如何设计dilation的数值也需要非常注意。

  解决上述问题的方法，可以参见如下两种：

• Hybrid Dilated Convolution (HDC)，参考链接：https://arxiv.org/pdf/1702.08502.pdf
• Atrous Spatial Pyramid Pooling (ASPP)，参考链接：https://arxiv.org/pdf/1706.05587v1.pdf

2. 深度学习经典网络模块

  以下是论文中出现的一些经典网络模块，具体原理和内容在此不深入介绍，主要介绍一下结构及实现。
  之所以将这些模块单独提出来，是因为深度学习真的是一门需要经验积累的学科。通过浏览深度学习的历史进程可以让我们站在巨人的肩膀上，大大增加我们的经验积累。但是如果只是单独将模块放在论文解析中介绍，或许就很容易迷失在论文各种复杂的网络设计、网络训练方法等细节上。因此，我认为把每篇论文最经典的网络模块部分单独提出来，纵向对比思考，有助于加深对深度学习网络模块进化的认知。

2.1 NiN块——cccp层(cascaded cross channel parametric pooling)

  本质上，就是对$m\times n\times k$的数据进行卷积操作后，再对feature map每个位置的多通道数据进行多层感知机(MLP)处理，在具体实现时，其实就是在卷积层后再增加2个$1\times 1$的卷积层，注意，每个卷积层之后还需要增加ReLU等非线性激活函数。具体结构如下：
  具体代码实现就不贴了，这个模块其实很简单的。但是NIN网络之所以不火，其实还是因为效果提升不是很明显，作者提出MLPConv层，其实是希望在普通的卷积层后增加多层感知机结构来提高卷积层的非线性输出能力。这种思路和方法还是非常具有学习意义的，因为之后的很多经典论文如VGG,GoogLeNet，都参照了这一思想。

2.2 Inception块

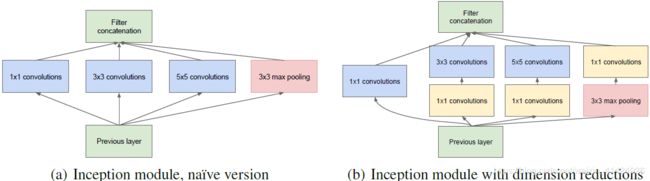  上图所示是论文“Going deeper with convolutions”中官方提供的Inception模块结构示意图(题外话，Inception是根据电影盗梦空间命名的)。左图是该模块最原始的设计思想，很直观可以理解到，设计者是希望对不同感受野的卷积操作提取到的特征进行整合利用，相当于同一组数据进行多尺度的特征提取，然后再将提取到的信息进行整合。这其实就是Inception块的设计初衷。由于每条路径上的卷积核大小不同，而最后的输出需要叠加在一起(按通道方向叠加)，所以很明显，每个卷积操作和最大池化操作都进行了适当的Paddding和步长的选择，使得输出的数据在除了通道以外的两个维度的尺寸保持一致。
  而右图可以看到，是增加了三个$1\times 1$卷积层，目的是为了什么呢？从原始的Inception层可知，如果直接将四个路径提取的特征按通道叠加，那么越后面的网络，其通道数量可想而知会越来越大，对应输入卷积层的网络参数也就越来越多，这是我们所不希望发生的。因此，在进行卷积操作前，先用$1\times 1$的卷积层将输入数据的沿通道方向的特征进行整合，并降低其通道数(降维)，然后再进行卷积操作，从而保证输入$3\times 3,5\times 5$卷积层的输入数据通道数不会太大，大大降低网络参数。而池化层本身是没有增加额外参数的，所以理论上来说$1\times 1$卷积层放在池化层前或后对训练效率的影响不大。
  Inception模块首先是继承了NIN网络中，将网络卷积层模块化设计的思想，另外，还采用了其中提出的$1\times 1$卷积层整合信息，减少网络参数，提高网络的训练效率。
  Inception模块的代码实现如下

class Inception(nn.Module):
    def __init__(self,in_channels,k1_channels,k3_red_channels,k3_channels,k5_red_channels,k5_channels,pool_channels):
        """
        初始化需要输入一些参数构造Inception模块
        :param in_channels: 输入数据通道数
        :param k1_channels: 1x1卷积层的输出通道数
        :param k3_red_channels: 3x3卷积层之前的1x1卷积层的输出通道数
        :param k3_channels: 3x3卷积层的输出通道数
        :param k5_red_channels: 5x5卷积层之前的1x1卷积层的输出通道数
        :param k5_channels: 5x5卷积层的输出通道数
        :param pool_channels: 池化层的输出通道数
        :param pool_conv1_channels: 池化层后的1x1卷积层的输出通道数
        """
        super(Inception,self).__init__()
        self.Line1 = nn.Sequential(
            nn.Conv2d(in_channels,k1_channels,1),
            nn.BatchNorm2d(k1_channels),
            nn.ReLU()
        )
        self.Line2 = nn.Sequential(
            nn.Conv2d(in_channels,k3_red_channels,1),
            nn.BatchNorm2d(k3_red_channels),
            nn.ReLU(),
            nn.Conv2d(k3_red_channels,k3_channels,3,padding=1),
            nn.BatchNorm2d(k3_channels),
            nn.ReLU()
        )
        self.Line3 = nn.Sequential(
            nn.Conv2d(in_channels,k5_red_channels,1),
            nn.BatchNorm2d(k5_red_channels),
            nn.ReLU(),
            nn.Conv2d(k5_red_channels,k5_channels,5,padding=2),
            nn.BatchNorm2d(k5_channels),
            nn.ReLU()
        )
        self.Line4 = nn.Sequential(
            nn.MaxPool2d(3,stride=1,padding=1),
            nn.Conv2d(in_channels,pool_channels,1),
            nn.BatchNorm2d(pool_channels),
            nn.ReLU(),
            nn.Conv2d(pool_channels, pool_conv1_channels, 1),
            nn.BatchNorm2d(pool_conv1_channels),
            nn.ReLU()
        )

    def forward(self, inputs):
        """分别计算出四条路径的输出结果
        然后再将其按通道方向叠加起来"""
        x1 = self.Line1(inputs)
        x2 = self.Line2(inputs)
        x3 = self.Line3(inputs)
        x4 = self.Line4(inputs)
        return torch.cat([x1,x2,x3,x4],dim=1)

2.3 shortcut块和bottleneck块

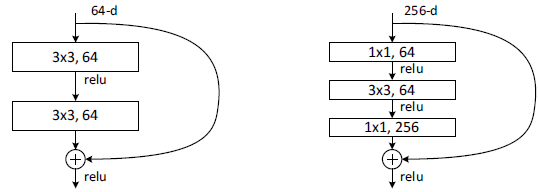
  普通的shortcut模块如上左图，可以看到，实质上就是将模块的输入和模块的输出相加，作为模块的最终输出。注意，这里是两个数据相加(矩阵元素与元素的对应相加，elementwise)，而不是沿通道方向叠加。要保证两者可以正常相加，就需要保证相加的两个矩阵维度尺寸一模一样，因此，其中的卷积层也是要增加适当的padding，保证数据尺寸一致。并且，如果卷积前和卷积后的数据通道数量发生了变化，那么在短路路径(就是图中的大弧线)上需要增加$1\times 1$卷积层，将输入数据的通道数进行匹配，保证两者的通道数也是相同的。另外，通常数据的通道数增加是伴随着数据另外两个维度的尺寸缩小的，因此，$1\times 1$卷积层也需要设定合适的步长来匹配相应维度的尺寸变化。关于这种短路输出与模块输出的数据尺寸匹配的方式，原论文提出了两种，identity mapping和projection mapping，详情可以参照"Deep Residual Learning for Image Recognition"
  上图右侧是改进的shortcut模块，作者称为"bottleneck building block"。为什么叫"bottleneck"(瓶颈)呢？其实非常生动形象，因为假设如图中所示，该模块的输入数据的通道数是256，那么在该模块中，先用$1\times 1$卷积层将通道降维成64，再进入卷积，卷积后再用$1\times 1$卷积层升维成原来大小的通道数，再与短路路径部分的数据相加。是不是有点像将一个很大的柔性物体从瓶颈处塞进瓶子的过程？(被瓶颈限制所以缩小，塞进去后又恢复为原来大小)。所以通常来说，"bottleneck"模块就是指这种数据先降维后升维的卷积操作，在很多其他论文里也经常可以看到。
  以"bottleneck"为基础的shortcut模块代码实现如下，该代码集成了输入输出数据尺寸变化与不变化两种情况。

class Deeper_Bottleneck(nn.Module):
    def __init__(self,in_channels,mid_channels,out_channels,stride=None):
        """
        Bottleneck模块
        :param in_channels: 输入模块的数据通道数
        :param mid_channels: 瓶颈处的数据通道数
        :param out_channels: 输出模块的数据通道数
        :param stride: 输出数据相对于输入数据的缩放倍数
        """
        super(Deeper_Bottleneck,self).__init__()
        self.stride = stride  # 如果stride!=None，说明该shortcut层发生了数据尺寸的变化
        if self.stride is not None:
            # self.project_shortcut是根据数据尺寸变化调整shortcut路径上的数据的短路层
            self.project_shortcut = nn.Sequential(
                nn.Conv2d(in_channels, out_channels, 1, stride=self.stride),
                nn.BatchNorm2d(out_channels),
                nn.ReLU()
            )
            self.Layer = nn.Sequential(
                nn.Conv2d(in_channels, mid_channels, 1),
                nn.BatchNorm2d(mid_channels),
                nn.ReLU(),
                nn.Conv2d(mid_channels, mid_channels, 3, stride=2, padding=1),
                nn.BatchNorm2d(mid_channels),
                nn.ReLU(),
                nn.Conv2d(mid_channels, out_channels, 1),
                nn.BatchNorm2d(out_channels),
                nn.ReLU()
            )
        else:  # 如果数据不发生尺寸变化，则进行正常的bottleneck模块处理，然后短路相加
            self.Layer = nn.Sequential(
                nn.Conv2d(in_channels, mid_channels, 1),
                nn.BatchNorm2d(mid_channels),
                nn.ReLU(),
                nn.Conv2d(mid_channels, mid_channels, 3, padding=1),
                nn.BatchNorm2d(mid_channels),
                nn.ReLU(),
                nn.Conv2d(mid_channels, out_channels, 1),
                nn.BatchNorm2d(out_channels),
                nn.ReLU()
            )

    def forward(self, inputs):
        x = self.Layer(inputs)
        if self.stride is None:
            return inputs+x
        else:
            return self.project_shortcut(inputs)+x

2.4 Dense块

  Dense模块其实和Shortcut模块非常类似，只是最后的两个数据相加修改成了沿通道方向叠加，通过这种方式，就可以将尺寸一致，通道数不同的各部分数据进行叠加整合，利用网络不同位置的特征进行学习。具体代码就不贴了。