贝叶斯规则

基本公式

全概率公式：设试验E的样本空间为S，A为E的事件，B1,B2,…,Bn为S的一个划分，并且P(Bi)>0(i=1,2,..,n) 那么：
P(A)=P(A|B1)P(B1)+P(A|B2)PB2)+…+P(A|Bn)P(Bn)

全概率公式证明依据：P(A)=P(AS)=P(AB1)+P(AB2)…+P(ABn)=P(A|B1)P(B1)+P(A|B2)P(B2)+….P(A|Bn)P(Bn)
S是样本空间，B1,B2,…,Bn是S的划分

贝叶斯公式：设试验E的样本空间为S，A为E的事件，B1,B2,..,Bn为S的一个划分，且P(A)>0,P(Bi)>0(i=1,2,3,…,n)那么：

贝叶斯公式分子证明依据（条件概率公式）：P(Bi|A)=P(BiA)/P(A) P(BiA)=P(A|Bi)P(Bi)
贝叶斯公式分母证明依据（全概率公式）

贝叶斯规则

贝叶斯规则以Thomas Bayes主教命名。
用来估计统计量的某种性质。
贝叶斯是用概率反映知识状态的确定性程度，数据集可以直接观测到，所以他不是随机的。

贝叶斯推断与其他统计学推断方法截然不同。它建立在主观判断的基础上，也就是说，你可以不需要客观证据，先估计一个值，然后根据实际结果不断修正。贝叶斯推断需要大量的计算。

http://www.ruanyifeng.com/blog/2011/08/bayesian_inference_part_one.html

贝叶斯定理

他是一种条件概率条件概率。 比如：在B发生时，A发生的可能性。
公式为：

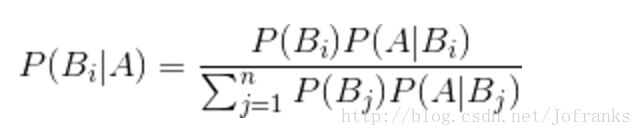
公式中，事件Bi的概率为P(Bi)，事件Bi已发生条件下事件A的概率为P(A│Bi)，事件A发生条件下事件Bi的概率为P(Bi│A)。
用来计算简单条件下发生的复杂事件。

条件概率

正如以上所说：在B发生时，A发生的可能性。 P(A|B)
通过韦恩图可以看到：

B发生时，A发生的概率：P(A|B)=P(A∩B)/P(B)
可以得到条件概率的推导过程如下：


等式合并：

最终得到：

P(类别|特征) = P(特征|类别)P(类别)/P(特征)

先验概率 后验概率

先验概率

根据以往经验和分析得到的概率。 往往作为 由因求果 问题中的 因 出现的概率。 又称： 古典概率

（在观测数据之前，我们将已知的知识表示成 先验概率分布 但是一般而言我们会选择一个相当宽泛的先验（高熵），反映在观测到的任何数据前，参数的高度不确定性）
（通常，先验概率开始是相对均匀的分布或高熵的高斯分布，观测数据通常会使后验的熵下降）

在上述贝叶斯公式中，我们把P(A)称为先验概率。 （B事件发生之前，对A事件概率的一个判断）
把P（A|B)称为后验概率。(事件B发生之后，对事件A概率的重新评估）
P(B|A)/P(B)称为：可能性函数。 这是一个调整因子，使得预估概率更接近真实概率。

后验概率

在一个通信系统中，在收到某个消息之后，接收端所了解到的该消息发送的概率称为后验概率。
他是在给出相关证据或者数据后得到的条件概率。
他指的是在得到结果的信息重新修正的概率。计算后验概率必须以先验概率为基础。

后验概率 = 先验概率 * 调整因子

似然函数

上述调整因子又叫 似然函数
他是关于统计模型参数的函数。
假定一个关于参数y，具有离散型概率分布P的随机变量X，则在给定X的输出x时，关于参数y的似然函数是：L(y|x)等于给定参数y后变量X的概率：
L(y|x) = P(X=x|y) = Py(x)

*概率：用于已知一些参数的情况下，预测接下来的观测所得到的结果。
似然：用于在已知某些观测所得到的结果时，对有关食物的性质的参数进行估计。
似然函数可以理解为条件概率的逆反。*

先验概率和后验概率区别

材料：
1：先验概率：利用现有材料计算的。
2：后验概率：利用先验概率+补充材料计算的。
计算：
1：先验概率：古典概率。
2：后验概率：使用贝叶斯公式，使用样本资料计算逻辑概率，还要使用概率分布，数理统计。

全概率.

将复杂事件概率求解 转化为： 不同情况下发生的简单事件概率的和。
用来计算复杂事件的概率。

定义：假设{Bn:n=1,2,3,…}是一个概率空间的有限或者无限的分割（既Bn为一完备事件组），且每个集合Bn是一个可测集合，则对任意时间A有全概率公式：

通过条件概率的推导可以看到:P(A∩B) = P(A|B)P(B) = P(B|A)P(A)
带入上述公式。

全概率公式，将对一复杂事件A的概率求解问题转换为在不同情况下或者不同原因Bn下发生的简单概率的求和问题。

全概率推导

现在我们有样本空间S，事件A，A‘和B。
韦恩图：

从上图给出：
P(B) = P(B∩A) + P(B∩A’)
将条件概率推导中的公式有：
P(B∩A) = P(B|A)P(A)
将上述公式合并：
P(B) = P(B|A)P(A) + P(B|A’)P(A’)

解释：如果A和A’构成样本空间，那么事件B的概率就是A和A’的概率分别乘以B对这两个事件的条件概率之和。
公式另一写法：

朴素贝叶斯

朴素贝叶斯算法是假设各个特征之间相互独立。

癌症测试（假阳性问题）

假设一种特定的癌症，发病率为人口的1%。
如果得了这种癌症，检查结果90%可能是呈阳性。
但是你并没有患癌症，检查结果还是呈阳性。所以，假设 如果你没有患上这种特定癌症，有90%可能性是呈阴性的。 这通常叫做 特异性。

问题：没有任何症状的情况下，你进行了检查，检查结果呈阳性， 那么你认为患上这种特定癌症的可能性是多少？
之前的癌症概率是 1%，敏感型和特殊性是 90%，癌症测试结果呈阳性的人患病的概率有多大？
是：百分之八又1/3

假定A事件表示得病，P(A)=0.001,这是先验概率。（没有做实验之前，我们预计的发病率）
假定B事件表示阳性，那么计算P=(A|B)，这是后验概率。（做了试验后，对发病率的估计）
P(A|B)=P(A)P(B|A)/P(B)
用全概率公式，改写分母：
P(A|B)=P(A)P(B|A)/(P(B|A)P(A)+P(B|A反)P(A反))

在上面，误报率是 10% （因为检查中90%是阴性，剩下10%是阳性。这里可能是误报的）

邮件分类

假设：现在我们有两个人A和B，两人写邮件都会用到love，deal，life这三个单词。
A使用三个单词的频率为：love=0.1,deal=0.8,life=0.1。
B使用三个单词的频率为：love=0.5，deal=0.2,life=0.3。
现在我们有很多封email，假设这封email作者是A或者B是等概率的，
现在有一封email，只包括life和deal两个词，那么这封邮件的作者是A或者B的概率。

计算先验概率
P(emailA) = P(lifeA)P(dealA)P(A) = 0.1* 0.8 * 0.5 = 0.04
P(emailB) = P(lifeB)P(dealB)P(B) = 0.3 * 0.2 * 0.5 = 0.03

当观察到life和deal两个词的条件下，作者是A或者B的概率
计算后验概率
P(emailA|”life,deal”) = P(emailA) * f(x)(似然函数) = 0.04 * (1/(0.04+ 0.03)) = 0.57
P(emailB|”life,deal”) = P(emialB) * f(x) = 0.03 * (1/(0.04+ 0.03)) = 0.43

全概率：
P(emailA|”life,deal”) + P(emailB|”life,deal”) = 1