【今日头条】二阶魔方
二阶魔方又叫小魔方,是2*2*2的立方形结构。每一面都有4个块,共有24个块。每次操作可以将任意一面逆时针或者顺时针旋转90°,如将上面逆时针旋转90°操作如下。
Nero在小魔方上做了一些改动,用数字替换每个块上面的颜色,称之为数字魔方。魔方上每一面的优美度就是这个面上4个数字的乘积,而魔方的总优美度就是6个面优美度总和。
现在Nero有一个数字魔方,他想知道这个魔方在操作不超过5次的前提下能达到的最大优美度是多少。
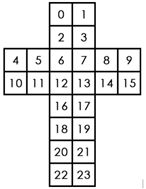
魔方展开后每一块的序号如下图:
输入描述:
输入一行包含24个数字,按序号顺序给出魔方每一块上面的数字。所有数大小范围为[-100,100]。输出描述:
输出一行包含一个数字,表示最大优美度。输入例子1:
2 -3 -2 3 7 -6 -6 -7 9 -5 -9 -3 -2 1 4 -9 -1 -10 -5 -5 -10 -4 8 2输出例子1:
8281解决方案:第一次接触这道题的时候,被搞的脑壳疼,主要是限时的情况下很急躁,思路完全打不开,写程序的大忌。改日静下心来仔细这道题目,其实也不难,只是过程很繁琐,就是bfs搜索解决,核心是怎么将魔方旋转时魔方方块的位置变动表达出来,解决这个剩下的就很好办了。
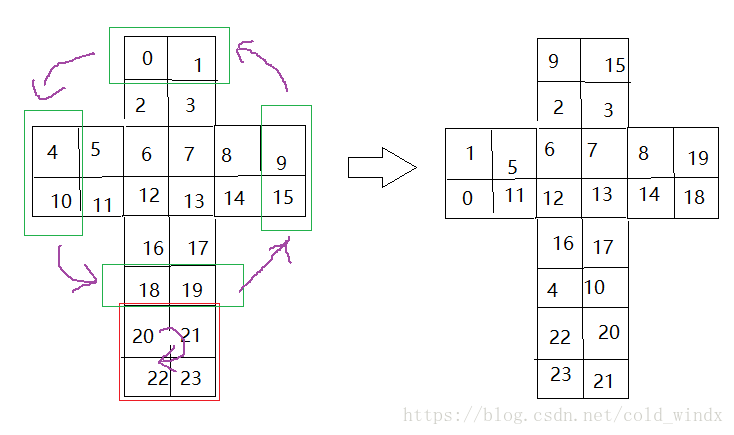
这里魔方直接用一个数组vec保存,假设魔方底面右旋一次,对应位置变换为:
同样,每一面的右旋都可以求出位置变换矩阵来,剩下的就是dfs求解的过程了。
#include
#include
#include
using namespace std;
const int n = 24;
//旋转位置矩阵
const int Rotate[6][24] = {
//FRONT
{0, 1, 11, 5, 4, 16, 12, 6, 2, 9, 10, 17, 13, 7, 3, 15, 14, 8, 18, 19, 20, 21, 22, 23},
//BEHIND
{9, 15, 2, 3, 1, 5, 6, 7, 8, 19, 0, 11, 12, 13, 14, 18, 16, 17, 4, 10, 22, 20, 23, 21},
//LEFT
{20, 1, 22, 3, 10, 4, 0, 7, 8, 9, 11, 5, 2, 13, 14, 15, 6, 17, 12, 19, 16, 21, 18, 23},
//RIGHT
{0, 7, 2, 13, 4, 5, 6, 17, 14, 8, 10, 11, 12, 19, 15, 9, 16, 21, 18, 23, 20, 1, 22, 3},
//UP
{2, 0, 3, 1, 6, 7, 8, 9, 23, 22, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 5, 4},
//DOWN
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 21, 20, 10, 11, 12, 13, 18, 16, 19, 17, 15, 14, 22, 23}
};
//魔方6个面
const int side[6][4] = {
{0, 1, 2, 3},
{4, 5, 10, 11},
{6, 7, 12, 13},
{8, 9, 14, 15},
{16, 17, 18, 19},
{20,21, 22, 23}
};
void rotateRC(vector& vec, int i)
{//旋转操作
vector tmp(vec);
for (int j = 0; j < n; ++j)
{
vec[j] = tmp[Rotate[i][j]];
}
tmp.clear();
}
long long getArea(const vector& vec)
{//求当前优美度
long long sum = 0, mul = 1;
for (int i = 0; i < 6; ++i)
{
for (int j = 0; j < 4; ++j)
{
mul *= vec[side[i][j]];
}
sum += mul;
mul = 1;
}
return sum;
}
long long dfs(vector vec, int count)
{
long long ans = getArea(vec);
if (0 == count) return ans;
for (int i = 0; i < 6; ++i)
{//旋转魔方6个面
vector tmp(vec);
rotateRC(tmp, i);
ans = max(ans, dfs(tmp, count - 1));
//逆时针旋转(顺时针旋转3次相当于逆时针旋转1次)
rotateRC(tmp, i);
rotateRC(tmp, i);
ans = max(ans, dfs(tmp, count - 1));
}
return ans;
}
int main()
{
vector vec(n);
for (int i = 0; i < n; ++i)
cin >> vec[i];
//dfs搜索
cout << dfs(vec, 5) << endl;
system("pause");
return 0;
}