机器学习——回归算法

一、线性回归算法

核心思想

线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。

一元线性回归：涉及到的变量只有一个
多元线性回归：涉及到的变量两个或两个以上

• 通用公式：
  $$h(w)=w_0+w_1{x}_1+w_2{x}_2+...=w^{T}x$$
  其中 $w,x$ 为矩阵，$w=\left(\begin{array}{c}{w}_0\\ w_1\\ w_2\\ ...\end{array}\right)$,$x=\left(\begin{array}{c}{x}_0\\ x_1\\ x_2\\ ...\end{array}\right)$

• 损失函数：
  $$J(\theta )=(h_w(x_1)-y_1{)}^2+(h_w(x_2)-y_2{)}^2+....+(h_w(x_m)-y_m{)}^2$$
  $$=\sum _{i=1}^m(h_w(x_i)-y_i{)}^2$$
  $y_i$为第$i$个训练样本的真实目标值，$h_w(x_i)$为第$i$个训练样本特征值的预测结果；
  也称为最小二乘法，一般用于度量预测结果与真实结果的误差。

LR 算法 API

• 正规方程
  sklearn.linear_model.LinearRegression()
  最小二乘法线性回归
  - 返回参数：coef_ 回归系数

• 梯度下降
  sklearn.linear_model.SGDRegression()

  SDG 最小化线性模型
  - 返回参数：coef_ 回归系数

• 回归评估

• 均方误差（Mean Squared Error）评价机制：
  $$MSE=\frac{1}{m}\sum _{i=1}^m(y^i-\bar{y}{)}^2$$
  注：$y^i$为预测值,$\bar{y}$为真实值

• API
  mean_squard_error(y_true,y_pred)
  注：此处预测值和真实值均为标准化之前的值

案例分析

import pandas as pd
import numpy as np
def linear():
    #获取数据
    from sklearn.datasets import load_boston
    lb=load_boston()

    #数据分割
    from sklearn.model_selection import train_test_split
    x_train,x_test,y_train,y_test=train_test_split(lb.data,lb.target,test_size=0.25)    
    
    #特征值和目标值标准化处理
    from sklearn.preprocessing import StandardScaler
    std_x=StandardScaler()
    std_y=StandardScaler()
    x_train=std_x.fit_transform(x_train)
    x_test=std_x.transform(x_test)
    
    y_train=std_y.fit_transform(y_train.reshape(-1,1))
    y_test=std_y.transform(y_test.reshape(-1,1))
    
    #最小二乘法回归建模
    from sklearn.linear_model import LinearRegression
    lr=LinearRegression()
    lr.fit(x_train,y_train)    
    print('正规方程参数结果为:',lr.coef_)
    #inverse是将目标值转换为标准化前的数值，predic是获取模型预测值
    y_lr_predict=std_y.inverse_transform(lr.predict(x_test))
    print('正规方程预测测试集的房子价格:',y_lr_predict)
    #评估模型
    from sklearn.metrics import mean_squared_error
    print('正规方程MSE误差为:',mean_squared_error(std_y.inverse_transform(y_test),y_lr_predict))
    
    
    #SGD回归建模
    from sklearn.linear_model import SGDRegressor
    sgd=SGDRegressor()
    sgd.fit(x_train,y_train)
    print('梯度下降参数结果为:',sgd.coef_)
    #inverse是将目标值转换为标准化前的数值，predic是获取模型预测值
    y_sgd_predict=std_y.inverse_transform(sgd.predict(x_test))
    print('梯度下降预测测试集的房子价格:',y_sgd_predict)
    #评估模型(注意 MSE 中预测目标值和实际目标值都需要用标准化之前的值)
    from sklearn.metrics import mean_squared_error
    print('梯度下降MSE误差为:',mean_squared_error(std_y.inverse_transform(y_test),y_sgd_predict))
    return None

linear()

优缺点分析

线性回归是最为简单、易用的回归模型，从某种程度上限制了使用，但在不知道特征之间的关系的前提下，我们一般选用线性回归器作为首要选择。

• 两种线性回归方法比较

梯度下降	正规方程
大规模数据>10w	小规模数据
需要选择学习率$\alpha$	没有超参数
需要多次迭代	一次运算得出
特征数n 较大时也适用	需要计算$(X{X}^T{)}^{-1}$，如果特征数n 较大时运算代价较大。因为逆矩阵的时间复杂度为$O(n^3)$
适用于各种各样的模型	只适用于线性回归模型，不适用于岭回归、逻辑回归等模型

• 过拟合&欠拟合问题

• 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据之外的测试数据上拟合效果不好，此时认为这个模型出现了过拟合的问题；（模型过于复杂）
  可①进行特征选择，消除关联性大的特征，但这类较难；或也可②通过交叉训练，让所有数据都通过训练来弥补过拟合的问题；或使用L2正则化的方式（岭回归）；

• 欠拟合：一个假设在训练数据上不能获得更好的拟合，但是在训练数据外的测试数据上也不能获得好的效果，此时认为这个模型出现了欠拟合的现象。（模型过于简单）
  一般通过增加特征来解决；

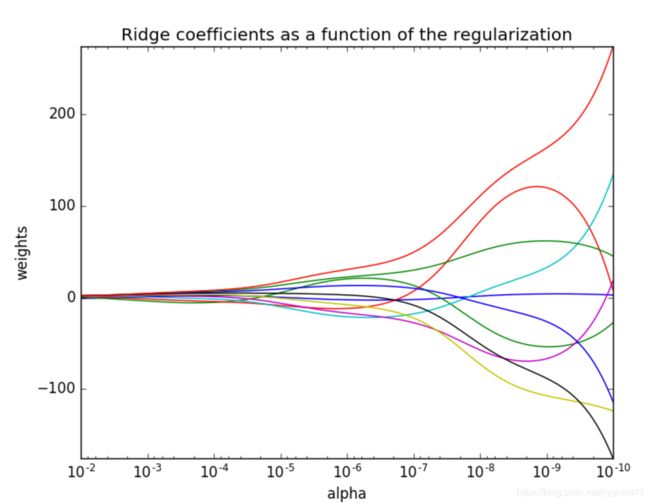
*岭回归

Ridge算法API

sklearn.linear_model.Ridge(alpha=1.0)

• alpha:正则化力度($\lambda$)

正则化力度

正则化力度越大，权重越小；

案例分析

import pandas as pd
import numpy as np
def linear():
    #获取数据
    from sklearn.datasets import load_boston
    lb=load_boston()

    #数据分割
    from sklearn.model_selection import train_test_split
    x_train,x_test,y_train,y_test=train_test_split(lb.data,lb.target,test_size=0.25)    
    
    #特征值和目标值标准化处理
    from sklearn.preprocessing import StandardScaler
    std_x=StandardScaler()
    std_y=StandardScaler()
    x_train=std_x.fit_transform(x_train)
    x_test=std_x.transform(x_test)
    
    y_train=std_y.fit_transform(y_train.reshape(-1,1))
    y_test=std_y.transform(y_test.reshape(-1,1))
    
    
    #岭回归建模
    from sklearn.linear_model import Ridge
    rd=Ridge(alpha=1.0)
    rd.fit(x_train,y_train)
    y_rd_predict=std_y.inverse_transform(rd.predict(x_test))
    #评估模型(注意 MSE 中预测目标值和实际目标值都需要用标准化之前的值)
    from sklearn.metrics import mean_squared_error
    print('岭回归MSE误差为:',mean_squared_error(std_y.inverse_transform(y_test),y_rd_predict))
    return None
linear()

二、逻辑回归算法

核心思想

• 损失函数
  与线性回归原理相同，但是由于逻辑回归是二分类问题，损失函数不一样，只能通过梯度下降来求解。
  对数似然损失函数：
  $$cost(h_{\theta }(x),y)=\{\begin{array}{ll}-log(h_{\theta }(x))& \text{if y=1}\\ -log(1-h_{\theta }(x))& \text{if y=0}\end{array}$$
  完整的损失函数
  $$cost(h_{\theta }(x),y)=\sum _{i=1}^m-y_{i}log(h_{\theta }(x))-(1-y_i)log(1-h_{\theta }(x))$$

  cost 损失的值越小，那么预测的类别准确度越高。
  目前逻辑回归求解损失函数，只能使用梯度下降的方法，但该方法存在一定弊端，即当损失函数存在多个局部最小值时，无法获取其全局最小值点。解决方法一般有：

  • 1.多次随机初始化，多次比较最小值结果；
  • 2.求解过程中，调整学习率；
    

算法 API

sklearn.linear_model.LogisticRegression(penalty=l2,C=1.0)

案例分析

def logistic():    
    #读取数据
    import pandas as pd
    data=pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data",
                     names=['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class'])
    #缺失值处理
    data=data.replace(to_replace='?',value=np.nan)
    data=data.dropna()
    #数据分割
    from sklearn.model_selection import train_test_split
    x_train,x_test,y_train,y_test=train_test_split(data[['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion', 'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses']],data['Class'],test_size=0.25)
    #特征工程
    from sklearn.preprocessing import StandardScaler
    std=StandardScaler()
    x_train=std.fit_transform(x_train)
    x_test=std.transform(x_test)
    
    
    #建立逻辑回归模型
    from sklearn.linear_model import LogisticRegression
    lg=LogisticRegression(C=1.0)
    lg.fit(x_train,y_train)
    
    #预测结果    
    print('LogisticRegression参数为',lg.coef_)
    print('准确率为:',lg.score(x_test,y_test))
    
    #精确率与召回率
    from sklearn.metrics import classification_report
    y_predict=lg.predict(x_test)
    print('召回率：',
          classification_report(y_test,y_predict,
                                labels=[2,4],
                                target_names=['良性','恶性']))
        
    return None
logistic()

优缺点分析

• 优点：
  适合需要得到一个分类概率的场景，简单，速度快；常常应用于广告点击率预测、是否患病、金融诈骗判断等问题；

• 缺点：
  只能处理二分类问题，不好处理多分类问题 ；

模型保存及加载

保存
joblib.dump(lr,'test.pkl')

加载
estimator=joblib.load('test.pkl')