读书笔记_《统计陷阱》达莱尔.哈夫

一、关于统计陷阱的一些角度

1.内在样本有偏

其根本问题是：样本是否足够代表总体？
其实际问题是：并非随机抽样
此类基本是民意调查难以避免的坑。
案例1：“1924级的耶鲁毕业生平均年收入有25111美元”
——这是问卷调查典型特征，能联系上的是一部分人，那些不能联系上的可能是年收入低的；能收回问卷的是一部分人，那些不寄回问卷的可能是年收入低的。再者，关于收入问题，大概大部分人都不会说实话或者虚高。
案例2：“以前曾经搞过一项旨在了解杂志阅读量的上门调查，其中的一个主要问题是：你和你的家人阅读什么杂志?当将调查结果制表并分析后发现：大部分的人喜欢《琴师》(Harper’s)，而没有多少人喜欢《真实故事》(True Story)。但出版商提供的数据却很明显地表明：《真实故事》的发行量是几百万份，而《琴师》只有几十万份。”
——这个调查我的理解是，被询问的人不一定是有购买意愿的人（文中说明是上门走访美国各式各样的居民区，但是我们的购买者其实只是有购买力有购买意愿的人甚至只是购买过的人）；并且“喜欢”这种意愿和是否购买完全是两个事情，当顾客做购买选择时会有诸多影响因素，价格、此时此刻心情、是否觉得有必要等等。另外，不同性质的杂志也没得比。
常见如街边调查、电话调查等都会存在有偏，一条街道是否能代替总体？那些不接收调研的受访者被代表了？调查员对受访者的挑选也有这样那些的观念。

2.精心挑选的平均数

其根本问题：什么时候选什么平均数（均值、中位数、众数）具有更好的描述性？
案例3：5月17日，腾讯发布了2017年第一季度业绩报告。财报显示，腾讯一季度总收入为495.52亿元，同比增长55%；经营盈利为192.72亿元，同比增长44%；期内盈利为人民币145.48亿元，同比增长57%；净利润率为29%，与去年持平。此外，财报还显示，腾讯截至3月31日共有39258名员工，第一季度平均月酬金为6.3万元。
——这种被平均的故事经年不息。。。像工资这种，基本都是右偏分布，平均数受右边的值影响很大，平均数>中位数>众数。这种状态说平均值能说明啥问题呢？啥都说明不了。此时用中位数来表达相对会更有意义一点。

3.没有披露的数据

其根本问题：样本不充分/所代表的意义资料不充分

案例4：一个典型的案例是几年前小儿麻痹症疫苗的实验。在一个社区里，450 名儿童接种了疫苗，而680 名儿童作为对照组没有接受疫苗。看上去，这是一个极大规模的医学实验。不久该区域感染了流行病，接种疫苗的儿童无一人患上小儿麻痹症。对照组的儿童也无一人患上该疾病。
在设计实验时，实验人员忽略了或者并没有真正理解该病的低发生率。在一般情况下，这种规模的小组中仅产生2 名患者。因此，实验从一开始便注定是毫无意义的。15～20 倍的样本容量也许才能产生足以解释某些事物的结果。
——也许450名儿童和680名儿童看上去是极大规模的实验，但相对于该病的低发生率，这个量级的样本结果也具有极大的偶然性，即使对照组有1人患上该疾病，这样的实验也是毫无意义。类似的，市面上很多调研报告基于几十个人就敢出的结论也是相当不可信的。

案例5:假设一对父母在《星期天》(Sunday)图画副刊等地方读到“孩子”将在某月份学会坐直的内容时，他们立刻会联想到自己的孩子。如果恰恰他们的孩子在该月份不能坐直，父母一定会得出结论：自己的孩子智力低下、不太正常或这很不公平等。

案例6：根据以往60 年的记录，俄克拉荷马城具有十分相似的平均温度——60．2 华氏度。但是，这个舒适凉爽的数字遮盖了130 华氏度的气温波动范围。
——案例5忽视了“某个月坐直”这个结论的误差，由于环境或教育的不同，实际不同个体是分散分布的，小于或大于某个月都是有的。案例6则中了均值的圈套，如果温度比较稳定尚可，若是存在巨大差异的地区，就不应该用均值来表达了。这些都是结论所代表的意义不够充分的情况。

4.毫无意义的工作

其根本问题：只有当差别有意义时才能称之为差别
案例7：经考试测量，彼得的智商98，琳达智商101，100为正常，是否意味着琳达比彼得要聪明？
——且不说智商考试所考核的是否只是某方面的，但平均智商是存在误差，例如误差在正负3，那么彼得智商在98+-3，琳达智商在101+-3，假设我们使用可能误差（1/2的数据落在1个标准误差内），意味着彼得有1/4的机会大于98+3，而琳达有1/4的机会小于101-3，彼得不一定就比琳达智商低。此类情况通常要注意抽样结果的范围，智力是否正常不会是一个值，而是一个范围，例如90~110，而相差不大的两个值相比没有任何意义。

5.惊人的统计图形

其根本问题：改变纵坐标的起点位置，或横向/纵向压缩
案例8：1938 年，《丹斯评论》(Dun's Review)的某个编辑曾从一则鼓吹华盛顿广告业的广告中摘录了一张统计图，图的标题是：“政府支出急剧上升!”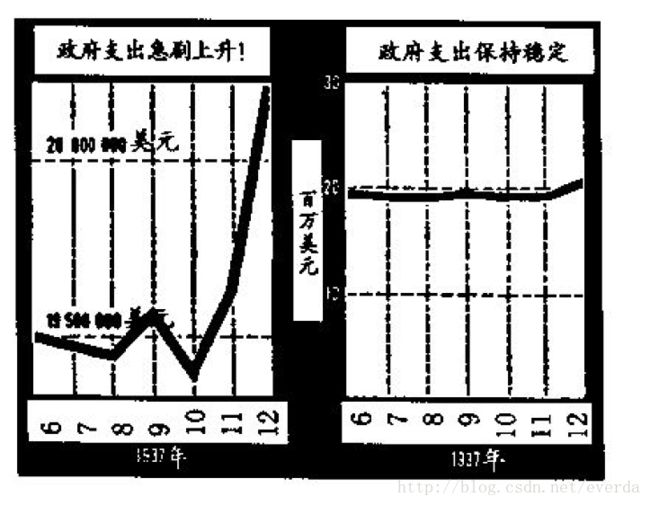

——可以看到左图在19.5百万美元~20百万美元之间，起始位置不是0；而右图同样在20百万美元上下波动。其实际大小和趋势都是一致的，但左图看起来惊人。另外右图将图形横向压缩，也会导致趋势看起来更加陡峭。

6.平面图形

其根本问题是：用图形代表两者比例是，只扩大高度比，而实际宽度也会跟着变，导致图片面积看着差距更大。
案例9：美国与罗坦提亚(Rotunda)木匠的平均周工资——进行比较，假设它们分别为60 美元和30 美元。

——如此可以看到，本来是1:2，右边图形高度是左边的2倍，但实际宽度也是左边的2倍，本要表达1:2，看着确是1:4的差距。
一般来说，不建议使用图形大小来表示比例，不说得控制图形尺寸，就是直观看大小也看不出具体比例是多少。直接用图形的数量表示即可，即美观又直观，如下图。

7.不相匹配的资料

其根本问题是：所要证明的事与所拿出的证据不相匹配，或者两个对比项的背景不相匹配
案例10：对著名内科医生香烟品牌调查的结果是：27%的被调查者选择了喉宝，该比例高于其他品牌。
——是否证明喉宝就比其他品牌危害性小呢？不一定，医生也不比其他人掌握更多关于香烟品牌是否危害性更小的资料。该案例所要证明的事是品牌的危害性哪个较小，只能通过成分分析来证明，却使用看起来应该更懂的医生的选择来证明，嗯，万一人家只知道喉宝呢？这跟危害性大小一毛钱关系都没有。
案例11：在美国与西班牙交战期间，美国海军的死亡率是9‰，而同时期纽约市居民的死亡率是16‰。后来海军征兵人员就用这些数据来证明参军更安全。如果假定这数据是正确的，那么促使这种差异产生的真正原因是什么?海军征兵人员根据两个数据的差异得出的结论是否正确?
——并不意味着去当海军安全，海军是身强力壮的男人；而同时期的纽约居民大都是老弱妇残，无论在哪死亡率都很高。这些数据根本不能说明符合参军标准的人在海军会比在其他地方有更高的存活机会。
此类问题类似的，还有不同时间的对比，由于不同时间的不同情况（例如某段时间大力抓某病例，导致该段时间该病例数量剧增，是否能意味着该病例在某段时间发生得最多？当然不能。）也可能导致对比没有意义。

8.相关关系和因果关系

其根本问题是：两变量具有数学上的相关关系，但不一定谁是因谁是果，更不一定有因果关系，有可能同为因果或者没有任何关联。
案例12：有人曾经高兴地指出：马萨诸塞州长老会的牧师收人与哈瓦那朗姆酒的价格之间存在着密切相关。
——孰因孰果?换句话说，是否牧师支持了朗姆酒贸易又或者牧师从此贸易中获益?这个结论未免过于牵强，一眼便可以识破。实际这个例子中，如果受到第三个因素一一历史性或全世界范围内物价水平上涨 的影响，那么收入和价格两个数据就都会上升。
另外，注意两个变量不同阶段的相关关系可能也不一样，例如雨下得越多， 谷物长得越高，收成越多；但暴雨则可能破坏谷物的增长，收成变少。

9.如何进行统计操纵

其根本问题是：如果不是故意，则通常是无知所导致的陷阱。除了懂统计的专家，描述数据的人往往是不懂统计的编辑、媒体、销售人员等，而且通常有利益相关。
除了以上角度和刻意挑选对自己利益有关的结论外，错误的假设逻辑、小样本容量使用百分比、基数不同都会引起误导。
案例13：1949年普查局公布的数据是“普通家庭的平均收入是3100美元”，而拉塞尔.塞奇基金会发布的“博爱的礼物”新闻故事里这个数据是5004美元。
——普查局用的是中位数，相对比较合理的算法。而后者将总收入除以1.49亿人得到人均1251美元，再乘4得出一个四口之家平均总收入为5004美元。
这个奇怪的算法一是使用了均值，而中位数实际相对小一些相对更具有代表性；二是假设了家庭收入与人口数成正比。。如果十口之家，岂不是上天了？

阅读统计资料时问自己五个问题

1.谁说的？

发声者所处位置和理解力通常对结论具有很大的影响，至于那些明显的PR文章就更不必说了。首先明白是谁说的，那么你心里大概就有个数了。

2.如何知道的？

总体是什么？样本是什么？询问的问题是什么？怎么得出的结论？

3.是否遗漏了什么？

是否存在样本有偏，引导性提问，样本容量太小、所证明的事与所调查的事不匹配、没有可信度检验、乱用基数等问题。

4.是否偷换了概念？

前后两个目的的同一样本调查得出的不同结论做对比，将实际不同用途的两种支出做对比（例如囚犯的生活费可能比旅店的租金高，就得出把囚犯安置在旅店更便宜？）等等。

5.资料是否有意义？

例如预测数据时，其前提是到目前为止的趋势都是事实，而未来的趋势只是猜测，其暗含着“其他所有条件都相同”，以及“现有趋势将继续下去”的前提。但事实上，条件总是在变化的，这种预测只能作为参考而已。

附思维导图：