来来来,一起来做四道面试真题
来来来,一起来做四道面试真题
1.导语
下面是前两天某哥们面某大厂的面试真题。
最大连续子序列
深拷贝带指向随机节点的链表
求32位整数中二进制1的个数
大数乘法
本节重点阐述这四道题的思路与实现,并在牛客上与Leetcode上找到了对应的题目,文中代码全部经过OJ过。
2.最长连续子序列
题目描述:
给定K个整数的序列{ N1, N2, ..., NK },其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj },其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个,例如给定序列{ -2, 11, -4, 13, -5, -2 },其最大连续子序列为{ 11, -4, 13 },最大和为20。现在增加一个要求,即还需要输出该子序列的第一个和最后一个元素。
输入描述:
测试输入包含若干测试用例,每个测试用例占2行,第1行给出正整数K( K< 10000 ),第2行给出K个整数,中间用空格分隔。当K为0时,输入结束,该用例不被处理。
输出描述:
对每个测试用例,在1行里输出最大和、最大连续子序列的第一个和最后一个元素,中间用空格分隔。如果最大连续子序列不唯一,则输出序号i和j最小的那个(如输入样例的第2、3组)。若所有K个元素都是负数,则定义其最大和为0,输出整个序列的首尾元素。
测试自己代码是否通过:
https://www.nowcoder.com/questionTerminal/afe7c043f0644f60af98a0fba61af8e7
解题思路:
上述简化:该子序列是最长的,且是连续的,且得返回最长连续子序列的左右端点,当存在多个结果时,返回第一种左右端点。
题目中给出,若所有K个元素都是负数,则定义其最大和为0,输出整个序列的首尾元素。当当前元素是负数时,当前位置的最大和就是0,每次更新最大和的时候,更新左右两端边界,右边界就是当前元素位置,左边界为从负数变为正数的分界点。得到状态方程:dp[k] = dp[k-1] + v[k]。如果dp[k]<=0,那么dp[k]就是0。
代码实现:
int main() {
int n;
cin >> n;
if (n == 0) {
cout << 0 << " " << 0 << " " << 0 << endl;
return 0;
}
vector v(n);
for (int i = 0; i < n; i++)
cin >> v[i];
vector dp(n);
// 检测是否全部小于等于0
bool flag = false;
for (int i = 0; i < n; i++) {
if (v[i] > 0) {
flag = true;
break;
}
}
// 全部小于等于0,那么总和就是0,i与j为左右边界
if (!flag) {
cout << 0 << " " << v[0] << " " << v[v.size() - 1] << endl;
return 0;
}
int i = 0, j = 0, max_res = -1;
// dp初始化
if (v[0] <= 0) {
dp[0] = 0;
i++; // i从下一位开始
} else {
dp[0] = v[0];
max_res = dp[0]; // 更新最大和
i = 0; // i从0开始
}
// 记录第一个最小的下界
int min_i;
for (int k = 1; k < n; k++) {
dp[k] = dp[k - 1] + v[k];
if (dp[k] <= 0) {
dp[k] = 0;
i = k + 1;
}
// 由于要输出第一个最小的下与上界,所以不能取等于号
if (dp[k] > max_res) {
j = k;
min_i = i;
max_res = dp[k];
}
}
cout << max_res << " " << v[min_i] << " " << v[j] << endl;
}
3.深拷贝带指向随机节点的链表
题目描述:
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
示例 1:
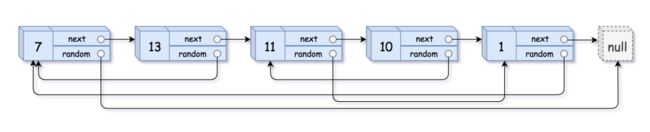
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
解题思路:
这道题考察的知识点非常多,单链表,图,树遍历~
怎么会牵扯到图与树呢,很简单啊~,上述多了个random指针,可以把一个节点包含next与random指针理解为树中节点有两个孩子,是不是就牵扯到树遍历呢,而当random构成一个环后,就形成了图,所以这道题牵扯的知识点多,考察的方向广,下面从不同角度来分析。
测试自己代码是否通过:
https://leetcode-cn.com/problems/fu-za-lian-biao-de-fu-zhi-lcof/
代码实现
(1)图的两种遍历
上述示例1的图:

可以构成一个图!对这个链表拷贝,是不是就转换成对图的拷贝呢~
DFS方法
从头结点开始拷贝,递归终止条件是head为空,为了保证一个节点只被一次拷贝,故在实现中我们需要使用一个键值对结构,key为原链表节点,value为拷贝后的结点,这样当这个节点访问过,就直接去键值对结构中取即可。然后递归拷贝所有的next与random结点。
时间复杂度:O(n),空间复杂度O(n)。
class Solution {
private:
// oldNode:newNode
map m; // 处理环
public:
Node *copyRandomList(Node *head) {
if (head == NULL) return NULL;
if (m.count(head) > 0) return m[head];
Node *cloneNode = new Node(head->val);
m[head] = cloneNode;
cloneNode->next = copyRandomList(head->next);
cloneNode->random = copyRandomList(head->random);
return cloneNode;
}
};
BFS方法
使用一个队列,将本题看成树的层次遍历,这样就简单了。还是需要用同DFS一样的键值对存储。先将头结点入队,当队列不为空时,弹出队首元素,若该节点的next结点未被访问,则拷贝 next 结点并加入队列;同理,如果该结点的 random 结点未被拷贝过,则拷贝 random 结点并加入队列;
时间复杂度:O(n),空间复杂度O(n)。
class Solution {
private:
// oldNode:newNode
map m; // 处理环
public:
Node *copyRandomList(Node *head) {
if (!head) return NULL;
queue q;
q.push(head);
Node *cloneNode = new Node(head->val);
m[head] = cloneNode;
while (!q.empty()) {
Node *cur = q.front();
q.pop();
// cur->next 并没有复制过
if (cur->next && m.count(cur->next) == 0) {
m[cur->next] = new Node(cur->next->val);
q.push(cur->next);
}
// cur->random并没有复制过
if (cur->random && m.count(cur->random) == 0) {
m[cur->random] = new Node(cur->random->val);
q.push(cur->random);
}
m[cur]->next = m[cur->next];
m[cur]->random = m[cur->random];
}
return cloneNode;
}
};
(2)迭代
迭代法
直接进行深拷贝,next指向新节点。如果新节点不存在,创建就行,否则直接返回,存在不存在就还是以键值对数据结构来存储。
时间复杂度:O(n),空间复杂度O(n)。
class Solution {
private:
// oldNode:newNode
map m; // 处理环
public:
Node *copyRandomList(Node *head) {
Node *oldHead = head;
Node *cloneNode = NULL;
while (oldHead) {
cloneNode = get(oldHead);
cloneNode->next = get(oldHead->next);
cloneNode->random = get(oldHead->random);
oldHead = oldHead->next;
cloneNode = cloneNode->next;
}
return m[head];
}
Node *get(Node *oldNode) {
if (!oldNode) return NULL;
Node *cloneNode;
if (m.count(oldNode) > 0) cloneNode = m[oldNode];
else {
cloneNode = new Node(oldNode->val);
m[oldNode] = cloneNode;
}
return cloneNode;
}
};
优化上述迭代
不用键值对数据结构来存储拷贝过的节点,而是在每个节点后面添加原节点的拷贝,例如:A->B->C 变成 A->A'->B->B'->C->C',然后进行断裂,得到A->B->C和A'->B'->C',最后返回 A'->B'->C'。
时间复杂度:O(n),空间复杂度O(1)。
class Solution {
public:
Node *copyRandomList(Node *head) {
if (head == NULL) return NULL;
Node *p = head;
// 构建新旧交替链表
while (p) {
Node *newNode = new Node(p->val);
newNode->next = p->next;
p->next = newNode;
p = newNode->next;
}
p = head;
// 连接random A->A'->B->B'->NULL
while (p) {
p->next->random = p->random ? p->random->next : NULL;
p = p->next->next;
}
Node *oldHead = head;
Node *newHead = head->next, *q = newHead;
p = oldHead;
// 断开新旧链表
while (p) {
p->next = p->next->next;
q->next = q->next ? q->next->next : NULL;
p = p->next;
q = q->next;
}
return newHead;
}
};
4.求32位整数中二进制1的个数
题目描述:
请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例 1:
输入:00000000000000000000000000001011 输出:3 解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
测试自己代码是否通过:
https://leetcode-cn.com/problems/er-jin-zhi-zhong-1de-ge-shu-lcof/
解题思路:
method1:easy写法,在面试中不可这样做。
class Solution {
public:
int hammingWeight(uint32_t n) {
int count=0;
while(n!=0) {
if((1&n)==1) count++;
n/=2;
}
return count;
}
};
method2:上述n/=2换成位运算n>>1会出问题。分析:对于负数,最高位为1,而负数在计算机是以补码存在的,往右移,符号位不变,符号位1往右移,最终可能会出现全1的情况,导致死循环。与0xffffffff相与,就可以消除负数的影响。与上0xffffffff之后的n是个正数,同负数的补码一样。
class Solution {
public:
int hammingWeight(uint32_t n) {
int count=0;
if(n<0) n = n&0xffffffff;
while(n!=0) {
count+=1&n;
n=n>>1;
}
return count;
}
};
解决上述问题,还可以用下面方法:
class Solution {
public:
int hammingWeight(uint32_t n) {
int count = 0;
int flag = 1;
while (flag != 0) {
if ((n & flag) != 0) {
count++;
}
flag = flag << 1;
}
return count;
}
};
method3:不存在移位操作,即不存在上述问题,那么可以采用n&(n-1)这样每次都会去掉一个1,上述代码优化为:
class Solution {
public:
int hammingWeight(uint32_t n) {
int count=0;
while(n!=0) {
count++;
n=n&(n-1);
}
return count;
}
};
根据该方法的拓展得到, 判断一个数是否是2的幂
bool powerof2(int n)
{
return ((n & (n-1)) == 0);
}
5.大数乘法
题目描述:
实现大数乘法,输入是两个字符串如 n1 = '340282366920938463463374607431768211456' n2 = '340282366920938463463374607431768211456' 输出 '115792089237316195423570985008687907853269984665640564039457584007913129639936' 要求:不能使用对大数相乘有内建支持的语言;需要包含对输入字符串的合法性校验
测试自己代码是否通过:
https://www.nowcoder.com/questionTerminal/6b668316f0ac4421ae86d7ead4301b42
解题思路:
面试的时候直接给的是大数乘法这四个字,应该想到转换成字符串来处理!
而字符串来说,需要处理一些特殊条件,例如:乘数为空或者被乘数为空,或者乘数为0,被乘数为0,那结果就是0,其余的按照两数相乘竖式来求。
具体实现过程中需要注意几点:
相乘结果位数不超过两个数位之和
当前位的数等于当前位的数+乘法结果+进位
当前保留位数为当前位的数与10取余
当前位进位为当前位的数除以10的结果
代码实现:
string bigMult(string a, string b) {
// 两个数为0或者一个为0
if (a.empty() || b.empty() || a.size() == 1 && a[0] == '0' || b.size() == 1 && b[0] == '0') return "0";
string res(a.size() + b.size(), '0');
// get res size
int len = res.size() - 1;
// 乘数
for (int i = a.size() - 1; i >= 0; i--, len--) {
// 乘后结果位置
int pos = len;
// 进位
int up = 0;
for (int j = b.size() - 1; j >= 0; j--, pos--) {
int multRes = (a[i] - '0') * (b[j] - '0');
// 当前位的数 = 当前位的数+乘法结果+进位
int temp = res[pos] + multRes + up - '0';
// 当前位保留值
res[pos] = temp % 10 + '0';
up = temp / 10;
}
// 是否有进位
if (up)
res[pos] = up + '0';
}
int k = 0;
while (res[k] == '0') k++;
return res.substr(k);
}
int main() {
string a, b;
cin >> a >> b;
cout << bigMult(a, b) << endl;
return 0;
}
![]()