卡方检验理论与特征选择实现

一.理论

1. 定义

卡方检验是一种用途很广的计数资料的假设检验方法。
它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。

2. 卡方检验的基本思想

卡方检验是以χ2分布为基础的一种常用假设检验方法，它的基本假设H0是：观察频数与期望频数没有差别。

2.1) 基本思想

1.首先假设H0成立。
2.基于此前提计算出χ2值，它表示观察值与理论值之间的偏离程度。
3.根据χ2分布及自由度可以确定在H0假设成立的情况下获得当前统计量及更极端情况的概率P。如果P值很小，说明观察值与理论值偏离程度太大，应当拒绝原假设，表示比较资料之间有显著差异；否则就不能拒绝无效假设，尚不能认为样本所代表的实际情况和理论假设有差别。

同一自由度下χ2越大，P越小。

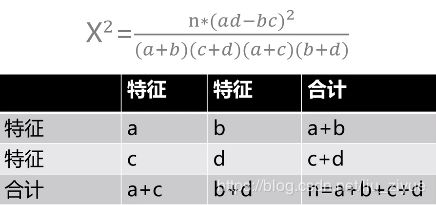
这里用一个通俗易懂的公式表示（公式分子表示差异程度，分母表示期望频数）：

接下来介绍两种比较特殊又比较常见的情况

2.2) 独立四格表

当样本是一张单独的四格表时，其卡方值用如下公式计算：

2.3) 八格表

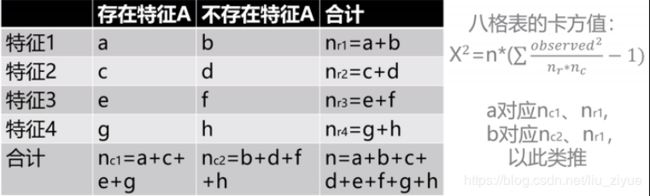
nr代表nr1、nr2、nr3、nr4，nc代表nc1、nc2。
例如a的nr、nc 就是nr：nr1，nc：nc1。

八格表的无效假设：特征1，特征2，特征3，特征4都与特征A没有关系，若观察频数与期望存在差异，则至少有一种特征与特征A存在关系。

2.4) 自由度

自由度指的是不受限制的变量的个数。
一般情况下，自由度=（行数-1）*（列数-1）

2.5) 卡方值的意义

χ2值中包含了：

1. 观察频数与期望频数偏差的平方大小，和差异程度与期望频数（理论值）的相对大小。
2. 当观察频数与期望频数完全一致时，χ2值为0；二者差异越大，χ2值越大。换言之，小的χ2值表明接近假设；大的χ2值表明远离假设。

2.6) 校正

当样本含量大于40但有理论频数小于5的情况时，卡方需要校正。公式如下：

一般认为列表中不宜有1/5以上数据的理论频数小于5，或有小于1的理论频数。若有，可用增大样本含量等方法调整数据。

二.案例

1. 例1

从某中学随机抽取两个班，调查他们对待文理分科的态度，结果，甲班37人赞成，27人反对；乙班39人赞成，21人反对，这两个班对待文理分科的态度是否有显著差异(α= 0.05)?

1.1) 建立假设检验

H0：r1＝r2，两个班对待文理分科的态度无显著差异
H1：r1 ≠ r2，两个班对待文理分科的态度有显著差异
α=0.05

1.2) Pyton实现

from  scipy.stats import chi2_contingency
import numpy as np
kf_data = np.array([[37,27], [39,21]])
kf = chi2_contingency(kf_data)
print('chisq-statistic=%.4f, p-value=%.4f, df=%i expected_frep=%s'%kf)

1. chisq-statistic=0.4054
2. p-value=0.5243
3. df=1
4. expected_frep=[[39.22580645 24.77419355]
   [36.77419355 23.22580645]]

1.3) 结论

由于p-value（0.5243）> α（0.05） 故接受原假设, 认为这两个班对待文理分科的态度无显著差别。

2. 例2(探究死亡年龄和居住地、性别是否有关)

2.1) 建立假设检验

H0：r1＝r2，死亡年龄和居住地、性别无关系
H1：r1 ≠ r2，死亡年龄和居住地、性别有关系
α=0.05

2.2) Pyton实现

from  scipy.stats import chi2_contingency
import numpy as np
kf_data = np.array([[11.7,8.7,15.4,8.4], [18.1,11.7,24.3,13.6],
              [26.9,20.3,37,19.3],[41,30.9,54.6,35.1],
              [66,54.3,71.1,50]])
kf = chi2_contingency(kf_data)
print('chisq-statistic=%.4f, p-value=%.4f, df=%i expected_frep=%s'%kf)

1. chisq-statistic=2.9208
2. p-value=0.9961
3. df=12
4. expected_frep=[[11.70042044 8.998674 14.46649418 9.03441138]
   [17.92123221 13.78303687 22.15795602 13.8377749 ]
   [27.39804334 21.07155563 33.87516171 21.15523933]
   [42.77800776 32.90012937 52.89107374 33.03078913]
   [63.90229625 49.14660414 79.00931436 49.34178525]]

2.3) 结论

因为p值=0.9961>0.05, 故接受原假设, 认为死亡年龄和居住地、性别无显著差别。

3. 例3(影响泰坦尼克号沉船事件乘客生存的重要因素)

3.1) Pyton实现

import pandas as pd
import numpy as np
# 特征最影响结果的K个特征
from sklearn.feature_selection import SelectKBest
# 卡方检验，作为SelectKBest的参数
from sklearn.feature_selection import chi2

df.columns=['乘客编号','存活','船舱等级','姓名','性别',
            '年龄','亲属数量','父母子女数','票的编号','票价',
            '座位号','登船码头']
df=df[['乘客编号','存活','船舱等级','性别',
            '年龄','亲属数量','父母子女数','票价','登船码头']].copy()
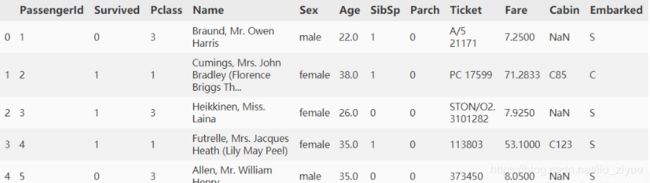
df.head()
y = df.pop("存活")
x=df
bestfeatures = SelectKBest(score_func=chi2, k=len(x.columns))
fit = bestfeatures.fit(x, y)
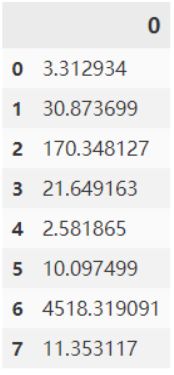
df_scores = pd.DataFrame(fit.scores_)
df_scores            

df_columns = pd.DataFrame(x.columns)
df_columns
# 合并两个df
df_feature_scores = pd.concat([df_columns,df_scores],axis=1)
# 列名
df_feature_scores.columns = ['feature_name','Score']  #naming the dataframe columns
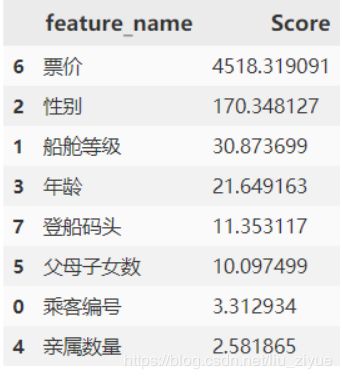
df_feature_scores
df_feature_scores.sort_values(by="Score", ascending=False)

3.2) 结论

可以看到影响特征（生存）的重要因素是票价、性别、船舱等级和年龄。