论文笔记——一种新的基于信任函数的K近邻分类方法
一种新的基于信任函数的K近邻分类方法
- 1、背景知识
- 1.1 信任函数
- 1.2、EK-NN
- 2、提出的BK_NN方法
- 2.1 构建BK_NN的bpa函数
- 2.2融合bpa函数
- 3、实例
1、背景知识
1.1 信任函数
1.2、EK-NN
2、提出的BK_NN方法
2.1 构建BK_NN的bpa函数
假设识别框架 Ω = { ω 0 , ω 1 , . . . , ω h } \Omega=\{\omega_0,\omega_1,...,\omega_h\} Ω={ω0,ω1,...,ωh}包含着一个孤立点 ω 0 \omega_0 ω0,首先对对象 x i {x_i} xi利用KNN寻找K近邻。在构建BBA的过程中,引入了与对象与其KNN之间距离有关的接受和拒绝阈值,如图所示。
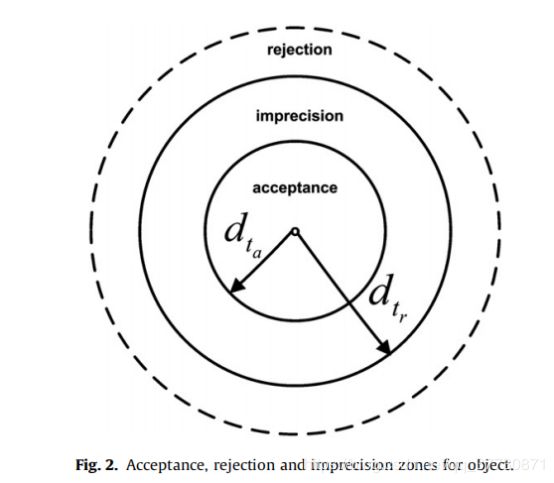
假设 x i {x_i} xi的最近邻 x j {x_j} xj的标签为 ω s {\omega_s} ωs, x i {x_i} xi和 x j {x_j} xj间的bpa函数基于每个类标签给出的接受阈值 d t a ω s {d^{\omega_s}_{t_a}} dtaωs以及拒绝阈值 d t r ω s {d^{\omega_s}_{t_r}} dtrωs:若 x i {x_i} xi和 x j {x_j} xj之间的距离 d i j {d_{ij}} dij比接受阈值 d t a ω s {d^{\omega_s}_{t_a}} dtaωs小,表明 x i {x_i} xi位于 ω s {\omega_s} ωs对 x j {x_j} xj的接受区, x i {x_i} xi将被认为最有可能属于 ω s {\omega_s} ωs类;若 d i j {d_{ij}} dij比拒绝阈值 d t r ω s {d^{\omega_s}_{t_r}} dtrωs大,意味着 x i {x_i} xi超出了拒绝区,所以 x i {x_i} xi不太可能属于 ω s {\omega_s} ωs类,它有更多的机会属于 ω s {\omega_s} ωs的互补集 ω s ‾ \overline{\omega_s} ωs;若 d i j {d_{ij}} dij处于两者之间,则认为 x i {x_i} xi处于不确定区域( ω s ⋃ ω s ‾ \omega_s\bigcup\overline{\omega_s} ωs⋃ωs)。基于以上概念,在此方法中,将bpa定义为与距离有关的函数:
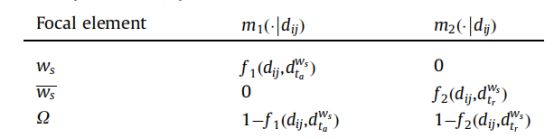
其中 d i j {d_{ij}} dij是 x i {x_i} xi和其最近邻 x j {x_j} xj的距离,函数 f 1 ( . ) {f_1(.)} f1(.)和 f 2 ( . ) {f_2(.)} f2(.) 将有效的BBA的良好(预期)行为描述为类,满足一下性质:
1、 f 1 ( . ) {f_1(.)} f1(.)单调递减,且 f 1 ( . ) ∈ [ 0 , 1 ] {f_1(.) \in[0, 1]} f1(.)∈[0,1];
2、若 d i j ≤ d t a ω s {d_{ij}\leq}d^{\omega_s}_{t_a} dij≤dtaωs,那么 f 1 ( d i j , d t a ω s ) ≥ 0.5 {f_1({d_{ij}},{d^{\omega_s}_{t_a}}) \geq0.5} f1(dij,dtaωs)≥0.5;
3、 f 2 ( . ) {f_2(.)} f2(.)单调递增,且 f 1 ( . ) ∈ [ 0 , 1 ] {f_1(.) \in[0, 1]} f1(.)∈[0,1];
4、若 d i j ≥ d t r ω s {d_{ij}\geq}d^{\omega_s}_{t_r} dij≥dtrωs,那么 f 2 ( d i j , d t r ω s ) ≥ 0.5 {f_2({d_{ij}},{d^{\omega_s}_{t_r}}) \geq0.5} f2(dij,dtrωs)≥0.5。
以下两个sigmiod函数可以满足上述四个条件并构造bpa函数:

Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。
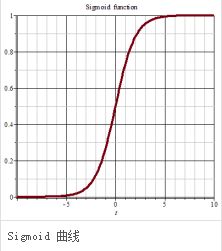
λ / 4 {\lambda / 4} λ/4 是拐点处切线的斜率。 d t a ω s {d^{\omega_s}_{t_a}} dtaωs和 d t r ω s {d^{\omega_s}_{t_r}} dtrωs是sigmiod函数拐点的横坐标。 在确定这些调谐参数时,可以首先计算 ω s {\omega_s} ωs中的每个训练数据与其kNN之间的平均距离。 在 ω s {\omega_s} ωs中,训练数据的所有平均距离的平均值 d ω s ‾ {d^{\overline{\omega_s}}} dωs可以用来确定 d t a ω s {d^{\omega_s}_{t_a}} dtaωs, d t r ω s {d^{\omega_s}_{t_r}} dtrωs和 λ s {\lambda_s} λs。

从实践中建议 γ t a ∈ [ 1 , 3 ] \gamma_{t_a}\in[1,3] γta∈[1,3], γ t r ∈ [ 2 γ t a , 3 γ t a ] \gamma_{t_r}\in[2\gamma_{t_a},3\gamma_{t_a}] γtr∈[2γta,3γta]。较大的接受阈值将导致更多的对象提交到元类中,较小的拒绝阈值将使更多的对象被视为孤点。由此方法可建立K个bpa函数,使用DS证据理论融合便可得到有关 x i {x_i} xi是否属于 ω s {\omega_s} ωs的证据。若xi不属于标签 ω p {\omega_p} ωp,那么 m ω p ( ω p ‾ ) = 1 {m^{\omega_p}(\overline{\omega_p}) = 1} mωp(ωp)=1。
2.2融合bpa函数
融合k个bpa函数共分为两步:
(1)与同一类相关联的BBA的子组合;
(2)关于不同类的子组合结果的全局融合。
第一步可以用DS方法融合。第二步,全局融合。假如一个对象有11个近邻有6个邻居在 ω 1 \omega_1 ω1类中居,有5个邻居在 ω 2 \omega_2 ω2类中。 这种对象通常被认为很难分类,为了解决该问题,将该对象划分为 ω 1 ⋃ ω 2 {\omega_1\bigcup\omega_2} ω1⋃ω2,表示不确定类。
假设k个近邻分别与h个类有关, [ k 1 , k 2 , . . . , k h ] [k_1,k_2,...,k_h] [k1,k2,...,kh]表示每个类对应的bpa函数的个数,第一步首先找到 k m a x = m a x ( k 1 , k 2 , . . . , k h ) k_{max}=max(k_1,k_2,...,k_h) kmax=max(k1,k2,...,kh)。若 k m a x − k i ≤ t , i = 1 , . . . , g k_{max}-k_i\leq t,i = 1,...,g kmax−ki≤t,i=1,...,g,对象很可能在类的联合中(元类)。
Ψ ( m a x ) = { ω i ∣ k m a x − k i ≤ t } \Psi(max) = \{\omega_i|k_{max}-k_i\leq t\} Ψ(max)={ωi∣kmax−ki≤t}对于对象xi来说是很难分类的。 然而,每个类中的KNN数量不足以确定对象的类,并且对象可能在一个类中,在罕见的情况下,它不包括在CMAX中。 为了解决此问题, ∣ Ψ ( m a x ) ∣ |\Psi(max)| ∣Ψ(max)∣所有基数小于或等于的元类都将被使用。

其中 η ∈ [ 0.1 , 0.3 ] \eta\in[0.1, 0.3] η∈[0.1,0.3]且 t ≥ 1 t\geq1 t≥1。 较大的t可以产生较少的错误分类错误,但通常会导致较大的元类。应该根据我们想要的结果的不精确和错误分类之间的预期折衷来确定t。所以全局融合策略为:
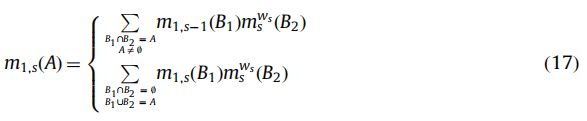
公式17得到的是一个未规范化的结果。 在DP规则中,焦点元素A可以是 Ω \Omega Ω的任何子集,而在我们的规则中,焦点元素A只能是特定的类、未知的类或仅是选定的元类(但不是所有可能的元类 meta_class)。 然后,一旦所有BBA的合并,(17)得到的未归一化融合结果将被归一化。 不属于元类的冲突mass函数将被重新分配给其他焦点元素。 然而,再分配方法在融合结果上并不重要,因为要重新分配的冲突mass函数通常很小,并且大多数冲突的mass函数通常属于选定的元类。归一化公式为:

如果没有选择元类,则全局融合规则将只剩DS规则。 然而,如果保留所有元类,则全局融合规则表现为DP规则,所有部分冲突 信任函数是为这些元类保留的。 这个全局融合规则可以被认为是DS规则和DP规则之间的折衷,因为只有部分元类根据实际情况选择可用。
在BK-NN算法中,需要三个调谐参数 γ t a \gamma_{t_a} γta, γ t r \gamma_{t_r} γtr和 η \eta η。 通过使用训练数据进行交叉验证,可以得到参数 γ t a \gamma_{t_a} γta和 γ t r \gamma_{t_r} γtr。
3、实例
给定识别框架 Ω = { ω 0 , ω 1 , ω 2 , ω 3 } \Omega=\{\omega_0,\omega_1,\omega_2,\omega_3\} Ω={ω0,ω1,ω2,ω3},对象 x i {x_i} xi有五个K近邻,其中三个近邻属于 ω 1 \omega_1 ω1,两个属于 ω 2 \omega_2 ω2。则得到与相应的BK-NN BBA建模:
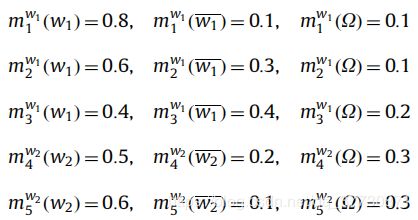
值得注意的是, 在计算焦点要素A的mass时 ω 1 ‾ = ω 0 ⋃ ω 2 ⋃ ω 3 \overline{\omega_1}={{\omega_0}\bigcup{\omega_2}\bigcup{\omega_3}} ω1=ω0⋃ω2⋃ω3, ω 2 ‾ = ω 0 ⋃ ω 1 ⋃ ω 3 \overline{\omega_2}={{\omega_0}\bigcup{\omega_1}\bigcup{\omega_3}} ω2=ω0⋃ω1⋃ω3, ω 3 ‾ = ω 0 ⋃ ω 2 ⋃ ω 1 \overline{\omega_3}={{\omega_0}\bigcup{\omega_2}\bigcup{\omega_1}} ω3=ω0⋃ω2⋃ω1。我们可以看到,5个近邻中没有一个在 ω 3 \omega_3 ω3类中,这表明 x i x_i xi不可能属于 ω 3 \omega_3 ω3。 因此,一个特定的BBA应该作为额外的引入:
![]()
m 1 ω 1 ( . ) m^{\omega_1}_1(.) m1ω1(.)、 m 2 ω 1 ( . ) m^{\omega_1}_2(.) m2ω1(.)、 m 3 ω 1 ( . ) m^{\omega_1}_3(.) m3ω1(.)与 ω 1 \omega_1 ω1相关, m 4 ω 1 ( . ) m^{\omega_1}_4(.) m4ω1(.)和 m 5 ω 1 ( . ) m^{\omega_1}_5(.) m5ω1(.)与 ω 1 \omega_1 ω1相关, (2)。分别使用Eq给出的DS规则将其融合,组合结果为:
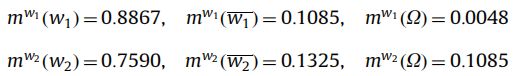
可得 k m a x = k 1 = 3 k_{max}=k_1=3 kmax=k1=3,假设 t = 2 t= 2 t=2, ∣ k 1 − k 2 ∣ = ∣ 3 − 2 ∣ < 2 |k_1-k_2|=|3-2|<2 ∣k1−k2∣=∣3−2∣<2, ∣ k 1 − k 3 ∣ = ∣ 3 − 0 ∣ = 3 |k_1-k_3|=|3-0|=3 ∣k1−k3∣=∣3−0∣=3,故 Ψ ( m a x ) = { ω 1 , ω 2 } \Psi(max) = \{\omega_1,\omega_2\} Ψ(max)={ω1,ω2},选中的类元则为 Ψ ( m a x ) = { ω 1 ⋃ ω 2 , ω 1 ⋃ ω 3 , ω 3 ⋃ ω 2 } \Psi(max) = \{\omega_1\bigcup\omega_2,\omega_1\bigcup\omega_3,\omega_3\bigcup\omega_2\} Ψ(max)={ω1⋃ω2,ω1⋃ω3,ω3⋃ω2}。则使用公式17全局的融合结果 m 1 ω 1 ( . ) m^{\omega_1}_1(.) m1ω1(.)、 m 2 ω 1 ( . ) m^{\omega_1}_2(.) m2ω1(.)以及 m 3 ω 1 ( . ) m^{\omega_1}_3(.) m3ω1(.)为:
因为没有冲突的信念要重新分配,组合结果已经标准化, 因此,我们不需要在这个特定的示例中使用(18)应用规范化步骤。 结果表明, x i x_i xi对元类 ω 1 ⋃ ω 2 \omega_1\bigcup\omega_2 ω1⋃ω2有最大的信任函数,也就是说,最可能属于它。