(源码)群体智能优化算法之正余弦优化算法(Sine Cosine Algorithm,SCA)
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 正余弦优化算法(Sine Cosine Algorithm,SCA)
- SCA
正余弦优化算法(Sine Cosine Algorithm,SCA)
该算法是由澳大利亚的Mirjalili于2016年提出的一种基于种群的新型随机优化算法,SCA创建多个初始随机候选解,然后利用基于正弦和余弦函数的数学模型,使得这些解朝最优解方向或反向波动。算法源代码可以关注公众号后回复"正余弦"获取。
SCA
SCA本质上为基于种群的优化算法,而基于种群的优化算法的共同点是都包含两个阶段:探索和利用。探索阶段,算法以较大的概率随机搜索以充分探索搜索空间,而在利用阶段,随机概率逐渐下降。
SCA使用以下两个等式进行位置更新:
X i t + 1 = X i t + r 1 × sin ( r 2 ) × ∣ r 3 P i t − X i t ∣ (1) X_{i}^{t+1}=X_{i}^{t}+r_{1} \times \sin \left(r_{2}\right) \times\left|r_{3} P_{i}^{t}-X_{i}^{t}\right|\tag{1} Xit+1=Xit+r1×sin(r2)×∣∣r3Pit−Xit∣∣(1)
X i t + 1 = X i t + r 1 × cos ( r 2 ) × ∣ r 3 P i t − X i t ∣ (2) X_{i}^{t+1}=X_{i}^{t}+r_{1} \times \cos \left(r_{2}\right) \times\left|r_{3} P_{i}^{t}-X_{i}^{t}\right|\tag{2} Xit+1=Xit+r1×cos(r2)×∣∣r3Pit−Xit∣∣(2)
其中 X i t X_{i}^{t} Xit为第 t t t次迭代中当前解在第 i i i个维度上的位置, r 1 r_1 r1/ r 2 r_2 r2/ r 3 r_3 r3为随机数, P i P_{i} Pi为第 i i i维终点的位置。
这两个等式通常按照如下的组合方式使用:
X i t + 1 = { X i t + r 1 × sin ( r 2 ) × ∣ r 3 P i t − X i t ∣ , r 4 < 0.5 X i t + r 1 × cos ( r 2 ) × ∣ r 3 P i t − X i t ∣ , r 4 ≥ 0.5 (3) X_{i}^{t+1}=\left\{\begin{array}{ll} X_{i}^{t}+r_{1} \times \sin \left(r_{2}\right) \times\left|r_{3} P_{i}^{t}-X_{i}^{t}\right|, & r_{4}<0.5 \\ X_{i}^{t}+r_{1} \times \cos \left(r_{2}\right) \times\left|r_{3} P_{i}^{t}-X_{i}^{t}\right|, & r_{4} \geq 0.5 \end{array}\right. \tag{3} Xit+1={Xit+r1×sin(r2)×∣r3Pit−Xit∣,Xit+r1×cos(r2)×∣r3Pit−Xit∣,r4<0.5r4≥0.5(3)
其中 r 4 r_4 r4为[0,1]之间的随机数。
可以看出,在SCA中主要涉及四个参数: r 1 r_1 r1, r 2 r_2 r2, r 3 r_3 r3和 r 4 r_4 r4。参数 r 1 r_1 r1为下一位置的所在区域(或移动方向),该区域既可以位于解和终点之间的空间内,也可以不在。参数 r 2 r_2 r2定义了朝向或背离终点的距离远近。参数 r 3 ∈ [ 0 , 2 ] r_3\in[0,2] r3∈[0,2]为终点引入了随机权重,以随机强调( r 3 > 1 r_3>1 r3>1)或弱化( r 3 < 1 r_3<1 r3<1)终点在距离计算时的作用。参数 r 4 r_4 r4用于以相等的概率在正弦和余弦之间进行切换。
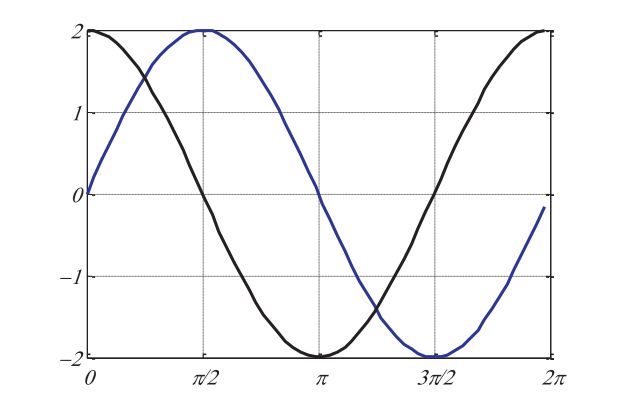
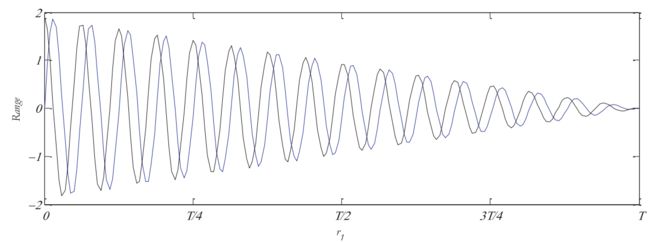
等式(1)和(2)中正弦和余弦对下一位置的影响如图1所示,正弦和余弦的周期模式可以允许一个解在另一个解周围重新定位,从而保证利用两个解之间定义的空间,同时为了探索搜索空间,解应该能够搜索其对应终点之间之外的空间,而这可以通过改变正弦和余弦函数的取值范围来实现,如图2所示。
图3展示了改变正余弦的取值范围可以更新解的位置,该随机位置到底是在空间内还是空间外,是通过等式(3)中定义的 r 2 ∈ [ 0 , 2 π ] r_2\in[0, 2\pi] r2∈[0,2π]来实现的。
为了平衡探索和利用,正弦和余弦的取值范围应该自适应地调整:
r 1 = a − t a T (4) r_{1}=a-t \frac{a}{T}\tag{4} r1=a−tTa(4)
其中 t t t为当前迭代, T T T为最大迭代次数, a a a是一个常数。图4展示了当 a = 2 a=2 a=2时取值范围递减的过程。
所以通过图3和图4可知,当取值范围在(1,2]和[-2,-1)范围内时,SCA算法在空间内进行探索,而当取值范围在[-1,1]之间时,SCA在空间内进行利用。
SCA算法的伪代码如下:
初始化初始解( X X X)
Do
评估每个代理的目标函数
更新当前最优解( P = X ∗ P=X^* P=X∗)
更新 r 1 r_1 r1, r 2 r_2 r2, r 3 r_3 r3和 r 4 r_4 r4
更新代理的位置(式3)
While( t t t<最大迭代次数)
Return全局最优解