机器学习笔记(二十八):高斯核函数
![]()
凌云时刻 · 技术
![]()
![]()
导读:核函数是机器学习算法中一个重要的概念。简单来讲,核函数就是样本数据点的转换函数。这一节我们来看看应用非常广泛的一个核函数,高斯核函数。
作者 | 计缘
来源 | 凌云时刻(微信号:linuxpk)
高斯核函数
![]()
高斯核函数的名称比较多,以下名称指的都是高斯核函数:
高斯核函数。
RBF(Radial Basis Function Kernel)。
径向基函数。
对于多项式核函数而言,它的核心思想是将样本数据进行升维,从而使得原本线性不可分的数据线性可分。那么高斯核函数的核心思想是将每一个样本点映射到一个无穷维的特征空间,从而使得原本线性不可分的数据线性可分。
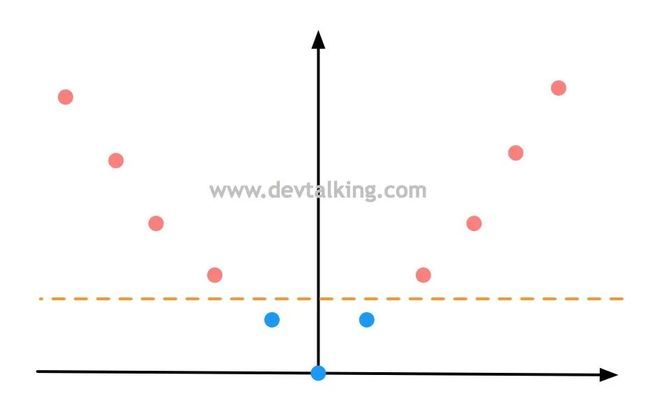
我们先来回顾一下多项式特征,如下图所示,有一组一维数据,两个类别,明显是线性不可分的情况:
然后通过多项式将样本数据再增加一个维度,假设就是 ,样本数据就变成这样了:
此时原本线性不可分的样本数据,通过增加一个维度后就变成线性可分的状态。这就是多项式升维的意义。
下面我们先来认识一下高斯核函数的公式:
上面公式中的 就是高斯核函数的超参数。然后我们再来看看高斯核函数使线性不可分的数据线性可分的原理。
为了方便可视化,我们将高斯核函数中的 取两个定值 核 ,这类点称为地标(Land Mark)。那么高斯核函数升维过程就是假如有两个地标点,那么就将样本数据转换为二维,也就是将原本的每个 值通过高斯核函数和地标,将其转换为2个值,既:
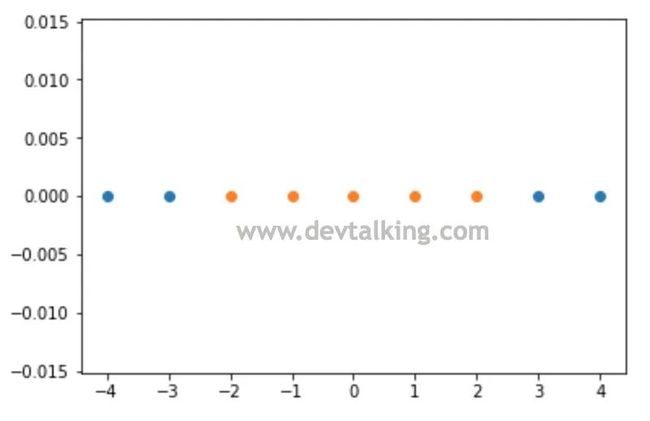
下面我们用程序来实践一下这个过程:
|
可以看到我们构建的样本数据是明显线性不可分的状态。下面我们来定义高斯核函数:
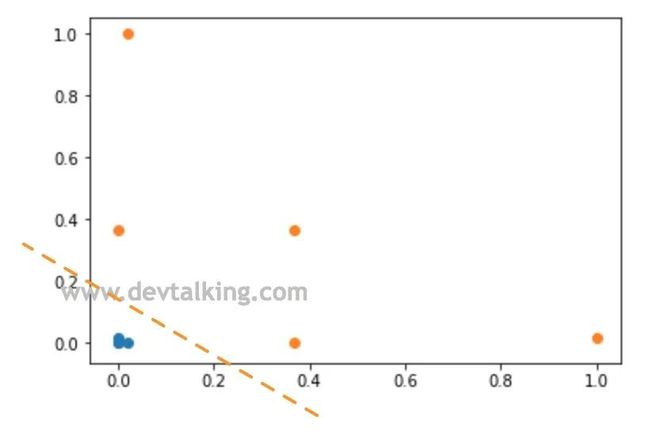
|
可以看到通过高斯函数将原本的一维样本数据转换为二维后,新样本数据明显成为线性可分的状态。
上面的示例中,我们将高斯核函数中的 取定了两个值 和 。在实际运用中,是需要真实的将每个 值带进去的,也就是每一个样本数据中的 都是一个地标,那么可想而知,原始样本数据的行数就是新样本数据的维数,既原始 的样本数据通过高斯核函数转换后成为 的数据。当样本数据行数非常多的话,转换后的新样本数据维度自然会非常高,这也就是为什么在这节开头会说高斯核函数的核心思想是将每一个样本点映射到一个无穷维的特征空间的原因。
 高斯核函数中的Gamma
高斯核函数中的Gamma
在看高斯核函数中的 之前,我们先来探讨一个问题,我们以前有学过正态分布,它是一个非常常见的连续概率分布,最关键的是它又名高斯分布,我们再来看看高斯分布的函数:
仔细看这个函数就能发现,它和高斯核函数的公式在形态上是一致的:
高斯函数 前的系数是 , 指数的系数是 。
高斯核函数 前的系数是1, 指数的系数是 。
所以高斯核函数的曲线其实也是一个高斯分布图。
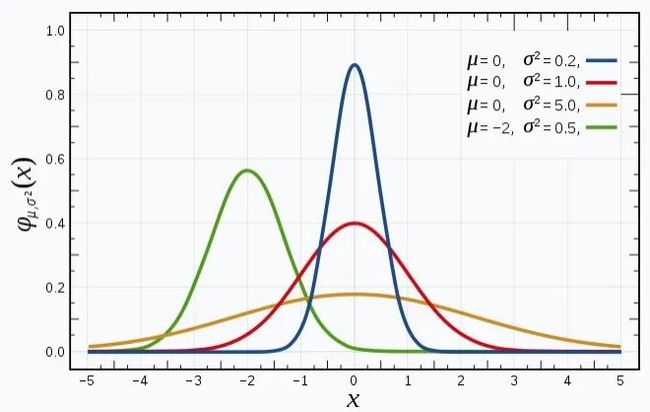
下面再来看看高斯分布图以及 和 对分布图的影响:
上图是维基百科对高斯分布解释中的分布图,从图中可以看到:
高斯分布曲线的形状都是相似的钟形图。
决定分布图中心的偏移情况。
决定分布图峰值的高低,或者说钟形的胖瘦程度。
因为高斯函数中的 和高斯核函数中 成倒数关系。所以:
高斯函数中 越大、高斯分布峰值越小。 越小、高斯分布峰值越大。
高斯核函数中 越大、高斯分布峰值越大,既钟形越窄。 越小、高斯分布峰值越小,既钟形越宽。
 Scikit Learn中的RBF SVM
Scikit Learn中的RBF SVM
这一小节来看看如果使用Scikit Learn中封装的RBF SVM。首先还是先构建样本数据,我们使用和多项式SVM相同的数据:
|
然后通过RBF SVM训练数据并绘制决策边界:
|
使用RBF SVM和使用多项式SVM其实基本一样,只是将SVC中的kernel参数由之前的poly变更为rbf,然后传入该核函数需要的超参数既可。
接下来绘制决策边界:
|
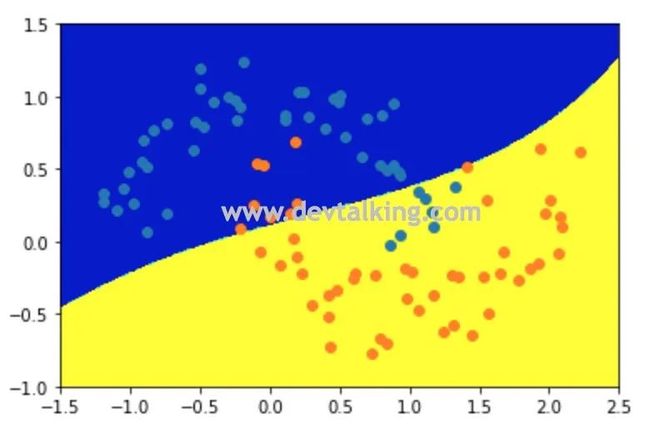
上图就是当 为1时,RBF SVM训练样本数据后的决策边界,我们先来解释一下它的高斯分布有什么关系。
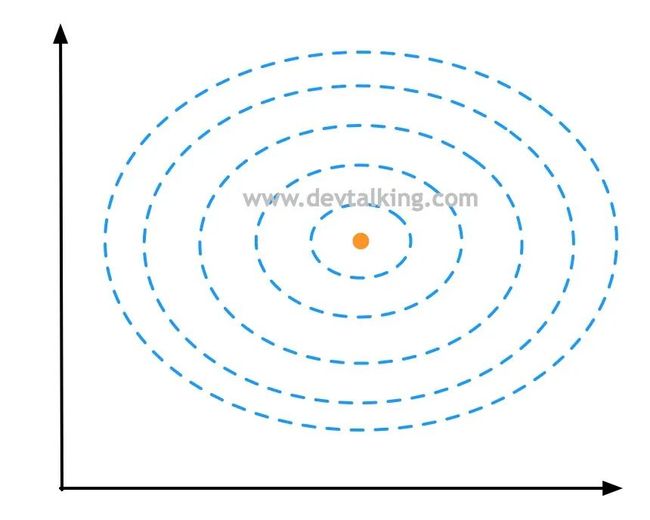
如上图所示,蓝色虚线表示等高线,橘黄色点表示一个样本点,所以上面的图其实是俯视以橘黄色样本点为峰值点的高斯分布图。
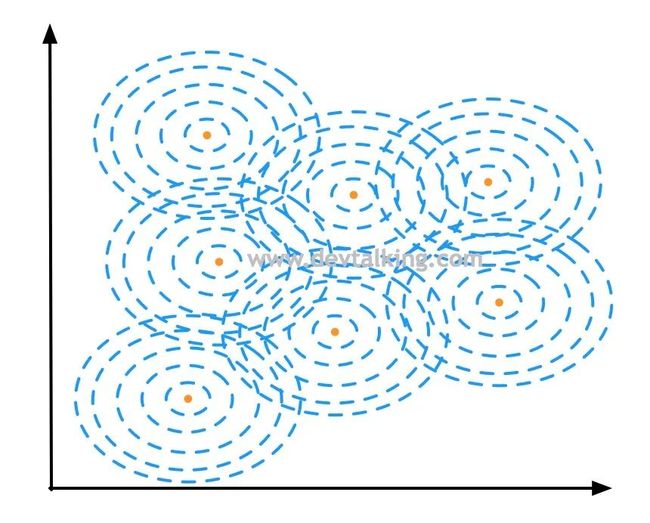
对于每个样本点都有围绕它的一个高斯分布图,所以连起来就形成了一片区域,然后形成了决策区域和决策边界:
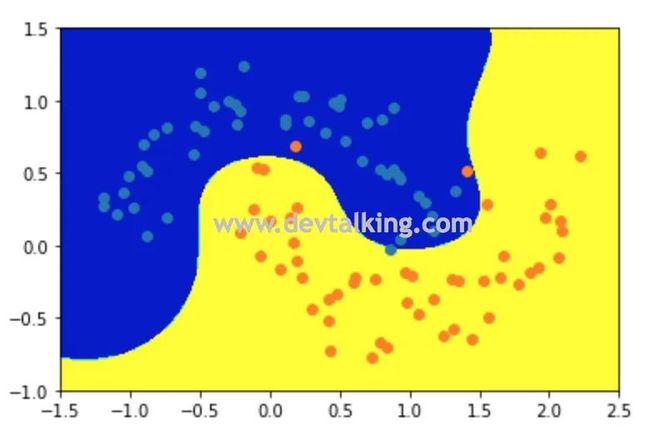
可以看到当 取1时,RBF SVM训练样本数据后的决策边界和多项式SVM的几乎一致。下面我们尝试变化超参数 来看看决策边界会有怎样的变化。
先来看看将 取较大值后的决策边界:
|
从上图可以看到,决策边界几乎就是围绕着蓝色点的区域,这也印证了高斯核函数中 越大、高斯分布峰值越大,既钟形越窄的定义。因为钟形比较窄,所以不足以连成大片区域,就呈现出了上图中的情况。
我们再来看看将 取较小值后的决策边界:
|
可以看到当 取0.1后,决策边界几乎成了线性决策边界,说明每个样本点的高斯分布钟形太宽了。所以我们得出结论,当 取值比较大时,数据训练结果趋于过拟合,当γγ取值比较小时,数据训练结果趋于欠拟合。
 SVM解决回归问题
SVM解决回归问题
SVM解决回归问题的思路和解决分类问题的思路正好是相反的。我们回忆一下,在Hard Margin SVM中,我们希望在Margin区域中一个样本点都没有,即便在Soft Margin SVM中也是希望Margin区域中的样本点越少越好。
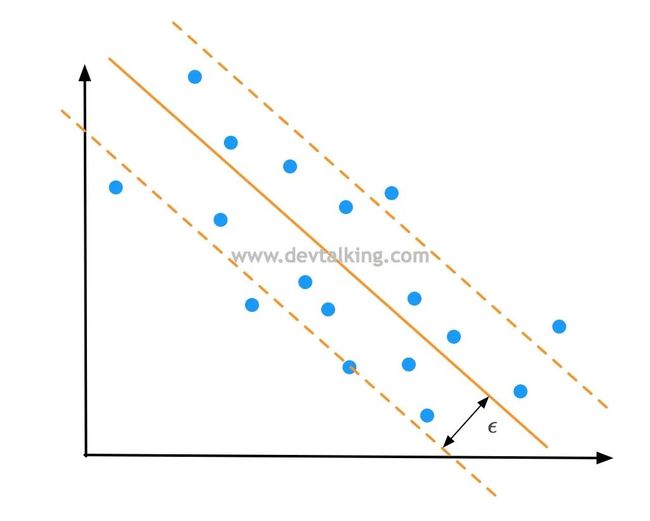
而在SVM解决回归问题时,是希望Margin区域中的点越多越好:
也就是找到一条拟合直线,使得这条直线的Margin区域中的样本点越多,说明拟合的越好,反之依然。Margin边界到拟合直线的距离称为 是SVM解决回归问题的一个超参数。
在Scikit Learn中有LinearSVR和SVR两个类,前者就是使用SVM线性方式解决回归问题的类,后者是SVM使用核函数方式解决回归问题的类。用法和LinearSVC及SVC的一致,只不过需要传入 这个超参数既可。
END
![]()
往期精彩文章回顾
![]()
机器学习笔记(二十七):核函数(Kernel Function)
机器学习笔记(二十六):支撑向量机(SVM)(2)
机器学习笔记(二十五):支撑向量机(SVM)
机器学习笔记(二十四):召回率、混淆矩阵
机器学习笔记(二十三):算法精准率、召回率
机器学习笔记(二十二):逻辑回归中使用模型正则化
机器学习笔记(二十一):决策边界
机器学习笔记(二十):逻辑回归(2)
机器学习笔记(十九):逻辑回归
机器学习笔记(十八):模型正则化
![]()
长按扫描二维码关注凌云时刻
每日收获前沿技术与科技洞见