算法训练 Collecting Luggage 计算几何 最短路

问题描述

　　航班结束后，提取行李的过程并不琐碎。手提箱和行李箱出现在一条传送带上，数百名乘客争夺有利的位置从中找到并取回自己的所有物。近日，成田机场管理局已决定使这一过程更加高效。在重新设计行李认领区前，他们需要一个模拟程序，使得乘客认领行李时的耗时更平均。这个模拟假定乘客们走一条由直线段组成的路径并使用最少的时间走到他们的行李处。
　　对于这个问题，传送带被描述为一个简单多边形。在传送带的某些点上出现一件行李，然后以恒定的速度沿着传送带移动。乘客一开始在一个传送带组成的多边形外的点。在行李出现的同时，乘客以恒定的速度（大于行李移动的速度）移动去提取行李。乘客的路径可以接触但不能穿过传送带，且能让乘客在最短的时间内和行李位于同一个点。
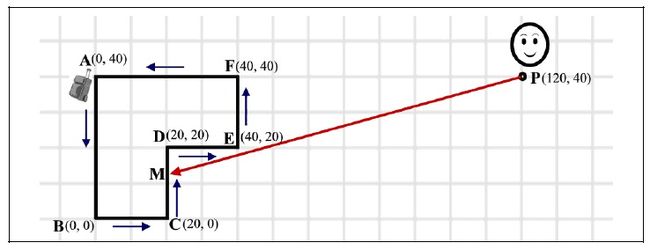
　　在接下来这幅图中，传送带被描述成多边形ABCDEF。行李开始在左上角（A点）并按时针方向沿多边形边缘移动，如小箭头所示。乘客一开始在P点，并开始按最短的时间能和行李到达同一点（图中M点）的路径移动。乘客的移动路径如红色箭头所示。该图对应第一个输入样例。

输入格式

　　输入包含一个或多个测试点来描述领取行李的场景。一个场景描述开头一行为一个单独的整数N(3<=N<=100)，多边形的顶点数。接下来N行每行两个整数x _i,y _i,(|x _i|,|y _i|<=10000)，按逆时针顺序给出多边形顶点的坐标。多边形是简单多边形，也就是说它不自交，不重合。多边形的描述后接下来一行两个整数p _x,p _y(|p _x|,|p _y|<=10000)，乘客起始位置所在点的坐标。接下来两个正整数V _L,V _P(0LP<=10000)，分别是行李和乘客的速度。所有坐标的单位是米，速度的单位是米/分钟。
　　你可以假设乘客位于多边形外。行李将会从多变形的第一个顶点开始按逆时针顺序沿传送带移动。
　　输入以一行一个单独的0结束。

输出格式

　　对于每组数据，输出一行，包括测试数据编号（从1开始编号）和乘客取得行李的最少时间。使用格式如样例输出所示（用冒号隔开分钟和秒），四舍五入到最近的整数。秒数占两位（不足用前导0补齐）。

样例输入

6
0 40
0 0
20 0
20 20
40 20
40 40
120 40
70 100
4
0 0
10 0
10 10
0 10
100 100
10 11
0

样例输出

Case 1: Time = 1:02
Case 2: Time = 12:36

数据规模和约定

　　对于10%的数据，给出的多边形保证是凸多边形
　　对于20%的数据，3<=n<=4
　　对于40%的数据，3<=n<=50
　　对于100%的数据，3<=n<=100，数组组数<=10，坐标绝对值、速度<=10000

个人思路：利用线段相交判断是否穿越传送带，利用二分法寻找最短路（个人只得了45分，希望大佬分享给我完整的思路和源码，我的源码只是为了抛砖引玉，勿喷，谢谢）
源码：

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {
	double eps=1e-6;
	List list=new ArrayList();
	public static void main(String[] args) {
		new Main().run();
	}
	class Vertex{
		double x;
		double y;
		public Vertex(double x,double y){
			this.x=x;
			this.y=y;
		}

	}
	public double getTime(Vertex x1,Vertex x2,int v){
		return Math.sqrt(Math.pow(x2.x-x1.x, 2)+Math.pow(x2.y-x1.y, 2))/v;
	}
	public double getDis(Vertex x1,Vertex x2){
		return Math.sqrt(Math.pow(x2.x-x1.x, 2)+Math.pow(x2.y-x1.y, 2));
	}
	public Vertex getMid(Vertex x1,Vertex x2){
		return new Vertex((x1.x+x2.x)/2, (x1.y+x2.y)/2);
	}
	public double min(double a, double b) { return a < b ? a : b; }  
	public double max(double a, double b) { return a > b ? a : b; }   
			
	//(ca x cd)·(cb x cd)<=0 则说明ca cb先对于cd的方向不同，则a b在线段cd的两侧，则相交 
	/**判断线段是否相交
	 * @param a 点
	 * @param b
	 * @param c
	 * @param d
	 * @return
	 */
	public boolean isIntersect(Vertex a,Vertex b,Vertex c,Vertex d){
		if(min(a.x, b.x) > max(c.x, d.x) || min(a.y, b.y) > max(c.y, d.y) || min(c.x, d.x) > max(a.x, b.x) || min(c.y, d.y) > max(a.y, b.y) ){
		    return false;   
		}
		 double h, i, j, k;   
		 h = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);   
		 i = (b.x - a.x) * (d.y - a.y) - (b.y - a.y) * (d.x - a.x);   
		 j = (d.x - c.x) * (a.y - c.y) - (d.y - c.y) * (a.x - c.x);   
		 k = (d.x - c.x) * (b.y - c.y) - (d.y - c.y) * (b.x - c.x);   
		 return h * i <= eps && j * k <= eps;   
	}
	/**是否共线
	 * @param a
	 * @param b
	 * @param c
	 * @param d
	 * @return
	 */
	public boolean isGongxian(Vertex a,Vertex b,Vertex c,Vertex d){
		double u;//分别记录两个向量
		u=(b.x-a.x)*(d.y-c.y)-(b.y-a.y)*(d.x-c.x);
		if(u==0){
			return true;
		}else{
			return false;
		}
	}
	/**判断点是否在多边形内
	 * @param p
	 * @return
	 */
	public boolean rayCasting(Vertex p){
		boolean flag=false;
		int next=0;
		for (int i = 0; i =p.y)||(s.y>=p.y&&t.yp.x){
					flag=!flag;
				}
			}
		}
		return flag?true:false;
	}
	/**判断是否穿越传送带
	 * @param a 起点
	 * @param p 终点
	 * @return
	 */
	public boolean judge(Vertex a,Vertex p){
		int next=0;
		int count=0;
		int G_count=0;
		int i=0;
		boolean re=false;
		for(;ip点到顶点达的时间  之间为有相遇点
		while(true){
			if((i+1)==vertexNum){
				next=0;
			}else if((i+1)<=vertexNum){
				next=i+1;
			}else{
				i=0;
				next=i+1;
			}
			l_time+=getTime(list.get(i),list.get(next),vl);
			p_time=getTime(list.get(next),p,vp);
			if(p_time>l_time){
				start_i=next;
				start_time=l_time;
			}else if(p_time==l_time){
				start_i=next;
				end_i=next;
				break;
			}else{
				end_i=next;
				break;
			}
			i++;
		}
		//计算相遇点坐标   二分法
		Vertex start=list.get(start_i);
		Vertex end=list.get(end_i);
		int count=0;
		double mid_time=0;
		Vertex mid = null ;
		while(count<50){
			mid = getMid(start, end);
			mid_time=getTime(p, mid, vp);
			new_time=start_time+getTime(list.get(start_i), mid, vl);
			if(new_time