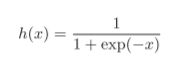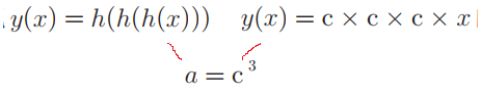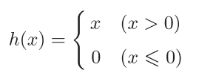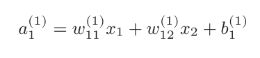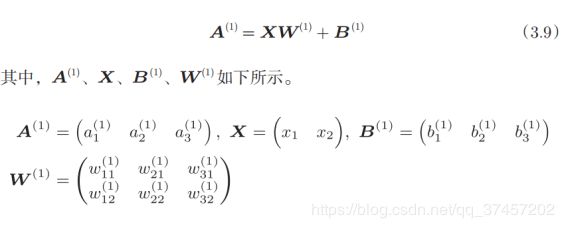神经网络基础学习笔记(二)神经网络
目录
三、神经网络
3.1 从感知机到神经网络
3.1.1神经网络例子:
3.1.2函数转换:
3.2激活函数
3.2.1激活函数类型:
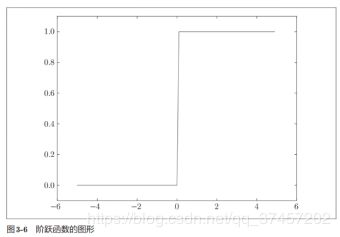
3.2.3 阶级函数的图形
3.2.2阶跃函数和sigmoid函数对比:
3.2.3ReLU函数:
3.3多维数组的运算:
3.3.1神经网络的内积:
3.4.三层神经网络的实现
3.5.1三中输出函数类型
3.5.2softmax函数溢出问题
3.5.3softmax函数特征:
3.5.4输出层的神经元数量
3.6手写数字识别
单处理与批处理
小结:
三、神经网络
解决问题:上一章能用与或非解决各种函数问题,但是权重是人工设定的,本章开始根据神经网络的实现,利用已有的数据学习合适的权重作为参数来解决上面的问题。
3.1 从感知机到神经网络
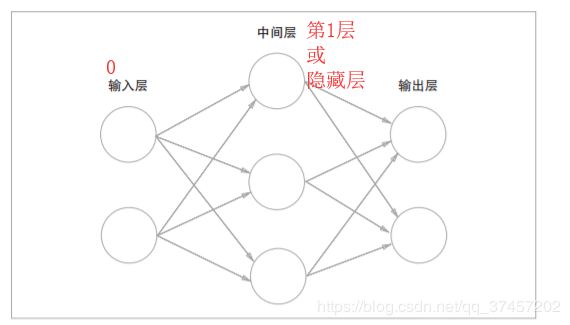
3.1.1神经网络例子:
神经网络实际跟感知机一样
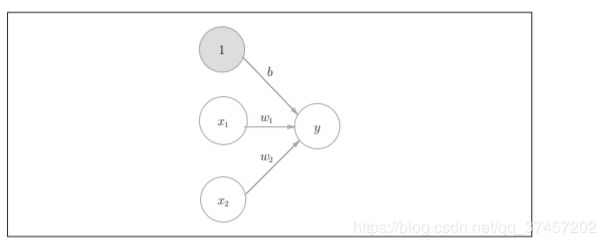
3.1.2函数转换:
借鉴:方同学整理的公式图
 图片来源: https://me.csdn.net/qq_37431224
图片来源: https://me.csdn.net/qq_37431224
根据上图的函数转换,我们就能转换为h(x),这就是激活函数
激活函数是连接感知机和神经网络的桥梁
3.2激活函数
3.2.1激活函数类型:
激活函数以阈值为界,一旦输入超过阈值,就切换输出。 这样的函数称为“阶跃函数”。
激活函数分为阶跃函数和sigmoid函数,其中阶跃函数就是当输入值超过某一阀值时就换转变输出。
其中exp(−x)表示![]() 的意思,h(x)也常用语分类的损失函数
的意思,h(x)也常用语分类的损失函数
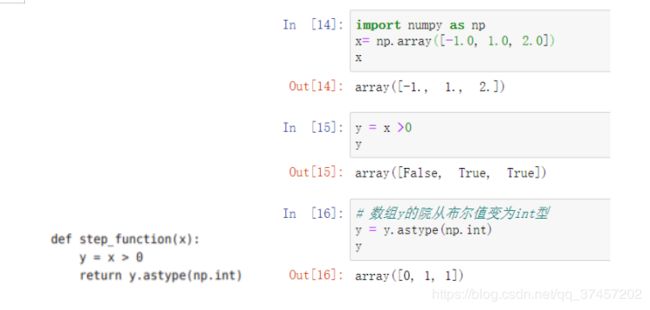
代码实现:
3.2.3 阶级函数的图形
阶跃函数与图像实现:
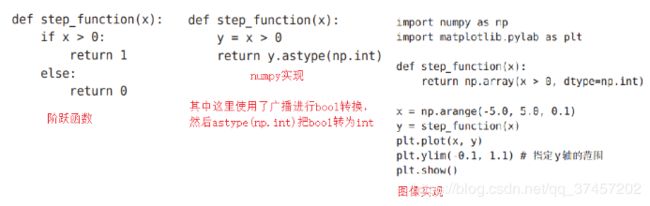 图片来源: https://me.csdn.net/qq_37431224
图片来源: https://me.csdn.net/qq_37431224
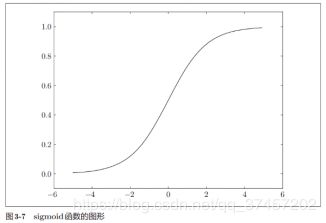
sigmoid函数图像:
3.2.2阶跃函数和sigmoid函数对比:
| 阶跃函数 | sigmoid函数 |
|---|---|
| 非平滑的 | 平滑的 |
| 只有2个值(二元值) | 无限个实数值 |
他们两者的相似点在于他们都处在0-1范围之间
神经网络的激活函数必须使用非线性函数。
另外sigmoid是非线性的曲线,不像线性函数(直线)h(x)=cx(c是常数),因为线性函数在多层感知机中是没有隐藏层的,如
一样是y=ax,无法发挥多层的优势。
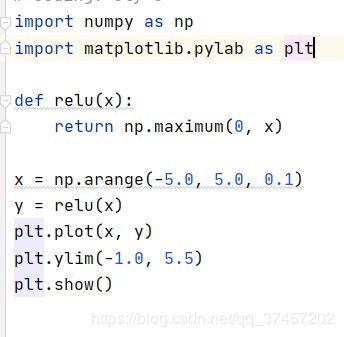
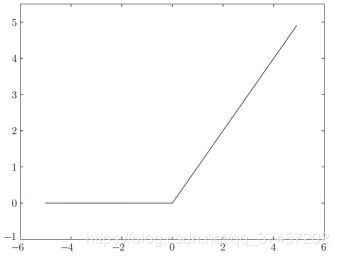
3.2.3ReLU函数:
大于0时直接输出x,小于等于0时输出0
函数实现:其中maxinum返回最大值
实现效果如图:
3.3多维数组的运算:
np.ndim(A) 输出A矩阵维数
np.shape 输出形状,既有几个构成。结果是个元组(tuple)。
3.3.1神经网络的内积:
使用np.dot(多维数组的点积),矩阵运算而已
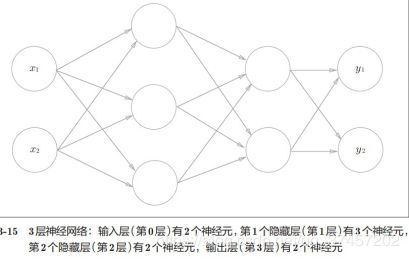
3.4.三层神经网络的实现
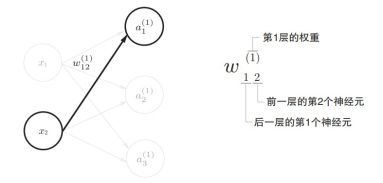
符号含义:
原理分析:
1)实现第0层到第一层:
所以有第一层的加权:
代码实现:
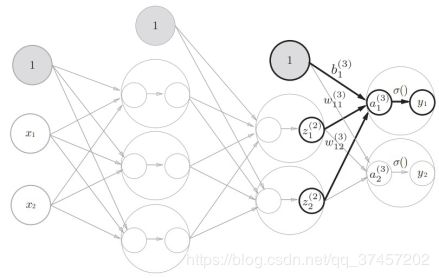
2)实现下图a1到z1构成激活函数h()的转变(sigmoid函数):
代码实现:
3)同理第一层到第二层一样,直接重复上面步骤:
代码实现:
4)第2层到第三层(输出层)也跟上面步骤基本一致,但激活函数不同:
 图片来源:方同学
图片来源:方同学
5)总体代码实现:
注意:一般地,回归问题可以使用恒等函数,二元分类问题可以使用 sigmoid函数, 多元分类问题可以使用 softmax函数。3.5输出层的设计:
3.5.1三中输出函数类型
1)恒等函数:就是直接原样输出,用在回归问题上
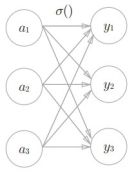
其中softmax函数表示在各输出之间都有收到输入信号的影响,如图:
代码实现:
3.5.2softmax函数溢出问题
我们都知道e^x当x很大时会出现爆炸性增长,这会导致溢出,所以我们要改进
3.5.3softmax函数特征:
我们可以看到输出的y都在0-1之间,且它们的和为1,所以我们可以把他转为概率问题,也就是说输出的越大,他的概率越高,从上图可以看出,y[2]最大,所以答案是第2个类别;另外e^x是一个单调递增函数,所以上例中a元素的大小关系和y的大小关系不变,y[2]最大,所以我们在实际上根本不需要softmax函数,直接看a元素就能知道哪个概率最大了(因为softmax需要指数运算,计算量挺大的)。
3.5.4输出层的神经元数量
由上图可以知道,输出神经元数量由类别数量决定,如输出结果为0-9这10个类别,那么神经元输出则为10个。
3.6手写数字识别
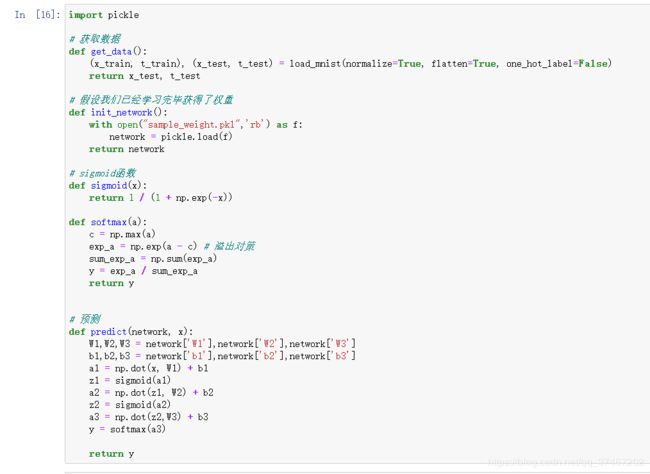
接下来,我们将我们的算法用于实际应用中,经典例子手写数字识别
代码注释如下,就不一一描述了。
load_mnist函数以“(训练图像 ,训练标签 ),(测试图像,测试标签 )”的 形式返回读入的MNIST数据。
神经网路输出
单处理与批处理
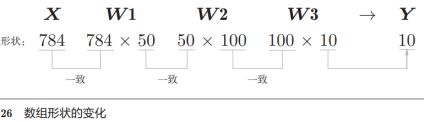
从上面的例子,我们知道输入层有784个神经元(28*28),输出层有10个神经元,假定隐藏层的1-2层有50个和100个神经元,我们有下面代码处理:
1)单处理:
利用上面一有的函数知识,我们现在正式可以判断其训练后的图片和标签之间的精确度啦:
2)批处理:
从上面(上图)的例子,我们知道1个图像输入(1*28*28)和输出(10个类别的概率)之后的矩阵形状
下面我们把以上面的例子一次性打包成100个图像进行计算
批处理的好处:每次我们计算一张时要io一次只拿1个图片,现在我们把一次的io拿100张来计算,因为计算速度比io速度快,所以批处理会在整体计算上变得更快
代码实现:
小结:
与上一章一样,我们不考虑具体权重如何求出,通过每一层的函数进行输出,这样就构成了一个简单的神经网络。
后期会对上面的参数进行讲解