一步步带你看懂orbslam2源码--单目初始化(三)

---

ORB-SLAM2目录：

   一步步带你看懂orbslam2源码–总体框架(一)
   一步步带你看懂orbslam2源码–orb特征点提取(二)
   一步步带你看懂orbslam2源码–单目初始化(三)
   一步步带你看懂orbslam2源码–单应矩阵/基础矩阵,求解R,t(四)
   一步步带你看懂orbslam2源码–单目初始化(五)

---

回顾:
  好久没更新啦,耽搁了这么久,实在是最近事情有点多,一直抽不出时间来写,趁着空闲之际,赶紧更新一波.上一节我们主要讲解了关于ORB特征点的原理以及源码中的实现,想必读完上节,大家应该对什么是ORB,怎么提取Oriented FAST关键点,怎么计算despritor以及如何进行四叉树存储,筛选高质量特征点,保证特征点提取的均匀性.
  接下来,有了图片的特征点信息之后,我们将正式进入Track();函数进行前端追踪,估计相机的POSE,创建关键帧等等.本文将讲解orb-slam2中的单目初始化,由于单目初始化设计内容较多,故将分为几次叙述.同时为了控制每章的规模,不至于文章太长导致读者们失去了阅读的兴趣.

---

理论环节

本质矩阵E/基础矩阵F

(1)对极约束

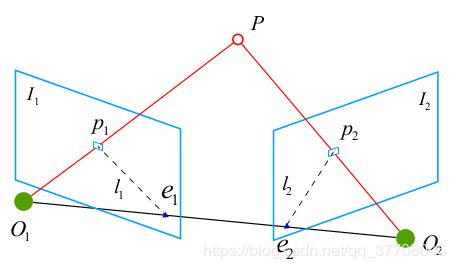
  如上图所示,空间中一点 $P$ 投影在$camera1$的成像平面$I_1$上的 $p_1$ ,同时投影在$camera2$的成像平面$I_2$上的 $p_2$ .其中, $l_1$ 和 $l_2$ 称为极线,$O_1$-$O_2$ 连成的线称为基线,由$O_1$-$O_2$-$P$组成的面称为极平面.由于投影在平面 $I_1$ 上的点 $p_1$ 拥有无穷多个可能的 $P$ ,且位于$O_1$-$P$ 的射线上.所以 $p_1$经过旋转变换投影到平面 $I_2$ 上的点 $p_2$ 可能位于极线 $l_2$ 上的任意一点,这就是所谓的对极约束,即由一个点投影后约束到一条线之上,幸好由于前面正确的特征点匹配,我们已经知道了$p_2$点的确确位置,所以反过来通过三角测量以及最小化重投影误差来求解 $P$ 点的位置以及两个 $camera$之间的$POSE$.

   注意:前提必须是正确的特征点匹配,错误的特征点匹配将导致错得离谱,到这里,读者们应该知道前端的特征点匹配对于系统的可靠性是有多么的重要了吧.

  接下来让我们来看看对极约束的数学表达,假设 $x_1$,$x_2$ 是两个像素点的归一化平面坐标,从$camera1$到$camera2$的旋转变换矩阵为: $T=[R|t]$,所以我们可以得到$$x_2=R{x}_1+t$$将上式同时左乘t^,可得:

   补充: $p_2^T{F}_{21}{p}_1=0$ ,可以写成 $p_2^T{l}_2=0$ ,表示 $p_2$ 在直线 $l_2$上,表示 $F_{21}$ 将 $p_1$ 投影到帧2图像中的直线 $l_2$ 上,这样子讲是不是可以更加准确的理解对极约束的物理意义呢?事实上,上面计算出来的基础矩阵 F 或者本质矩阵 E 都是表示了从帧1到帧2的变化,这在实际代码编程中将具有重要的意义.

(2)基础矩阵的计算

   参考"视觉SLAM十四讲"中的说明,根据定义矩阵$F$是一个3×3的矩阵,内有9个未知数.那么,是不是任意一个3×3的矩阵都可以被当成基础矩阵呢?从F的构造方式上看,有以下值得注意的地方;

• 本质矩阵是由对极约束定义的。由于对极约束是等式为零的约束,所以对 E 乘以任意非零常数后,对极约束依然满足.我们把这件事情称为 E 在不同尺度下是等价的.
• 本质矩阵 E 的奇异值必定是$[\sigma ,\sigma ,0{]}^T$的形式,这称为基础矩阵的内在性质.
• 另一方面,由于平移和旋转各有三个自由度,故$F$共有六个自由度.但由于尺度等价性,故$F$实际上有五个自由度.
     5个自由度矩阵的求解理论上最少可用五点对,但是实际操作中仍然采用八点法来进行求解,其本质上没有太大区别.假设一点对分别为:$p_2=(u_2,v_2,1)$ 和 $p_1=(u_1,v_1,1)$,根据对极约束可得.
  $$\left[\begin{array}{ccc}{u}_2& v_2& 1\end{array}\right]\left[\begin{array}{ccc}{f}_1& f_2& f_3\\ f_4& f_5& f_6\\ f_7& f_8& f_9\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right]=0\text{\hspace{1em}(1)}$$

化简可得:
$$u_1{u}_2{f}_1+u_1{v}_2{f}_2+u_1{f}_3+v_1{u}_2{f}_4+v_1{v}_2{f}_5+v_1{f}_6+u_2{f}_7+v_2{f}_8+f_9=0$$

将八点对联立起来构建成矩阵如下:
$$\left[\begin{array}{ccccccccc}{u}_1{u}_2& u_1{v}_2& u_1& v_1{u}_2& v_1{v}_2& v_1& u_2& v_2& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]\left[\begin{array}{c}{f}_1\\ f_2\\ f_3\\ f_4\\ f_5\\ f_6\\ f_7\\ f_8\\ f_9\end{array}\right]=0\text{\hspace{1em}(2)}$$

  由于匹配点之间本身存在误差,所以式(2)本身不会绝对成立.因此实际求解过程中采用最小特征值对应的特征向量来近似替代解.至今,可能很多同学就懵了,这是什么跟什么呀…
其实,根据特征值与特征向量的定义可知:
$$A\xi =\lambda \xi \text{\hspace{1em}(3)}$$
当特征值$\lambda$取0时,等式(3)右边等于0,左边的$\xi$不就是矩阵$A\xi =0$的解么,没错,就是我们所要求解的F矩阵.

单应矩阵

(1)概念

   讲完了对极约束,我们应该来讲讲单应矩阵了,单应矩阵也是非常重要的,毕竟对极约束并不能够解决所有的问题,当相机只有旋转没有平移时,可以使用单应矩阵估计相机运动.因为此时平移为0,计算出来的E或者F也为0,进而R=0,得到了错误解,而使用单应矩阵依然能够正确计算.单应矩阵主要用于当相机只有纯旋转运动,或者地图点在同一平面上时,或许我们可以形象地称之为"平面约束".

  本文讲的单应矩阵将和"视觉SLAM十四讲"中的有略微的区别,主要是用于后面介绍orb-slam2源码时能够完全匹配起来,不过并没有本质上的区别.

  已知一个平面方程 $Ax+By+Cz-d=0$ ,其中该平面的法向量 $n^T=(A,B,C{)}^T$ ,由于点 $P$ 位于该平面上,故有:$$n^{T}P-d=0$$稍加整理,得
$$\frac{n^{T}P}{d}=1$$
故
$$\begin{array}{rl}{p}_2& =K(RP+t)\\ & =K(RP+t\cdot \frac{n^{T}P}{d})\\ & =K(R+\frac{t{n}^T}{d})P\\ & =K(R+\frac{t{n}^T}{d})K^{-1}{p}_1\\ & =H_{21}{p}_1\end{array}$$
其中,单应矩阵 (注意单应矩阵的下标,表示从$camera1$ 到 $camera2$的单应矩阵变换):
$$H=K(R+\frac{t{n}^T}{d})K^{-1}$$

(2)单应矩阵的计算

  单应矩阵采用DLT线性化求解,由于单位矩阵的自由度为8,而一对匹配特征点可以提供两个约束,所以理论上最少可以用四点对进行求解.但是实际应用上其实用四点对或八点对都没有太大本质上的区别,已知一点对,$p_2=(u_2,v_2,1)$ 和 $p_1=(u_1,v_1,1)$,由单应矩阵变换关系可以得到 (等价于$p_2=H_{21}{P}_1$);
$$\left[\begin{array}{c}{u}_2\\ v_2\\ 1\end{array}\right]=\left[\begin{array}{ccc}{h}_1& h_2& h_3\\ h_4& h_5& h_6\\ h_7& h_8& h_9\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right]\text{\hspace{1em}(4)}$$进一步计算:
$$\left[\begin{array}{c}{u}_2\\ v_2\\ 1\end{array}\right]=\left[\begin{array}{c}{h}_1{u}_1+h_2{v}_1+h_3\\ h_4{u}_1+h_5{v}_1+h_6\\ h_7{u}_1+h_8{v}_1+h_9\end{array}\right]\text{\hspace{1em}(5)}$$所以:
$$\{\begin{array}{rl}{u}_2& =\frac{h_1{u}_1+h_2{v}_1+h_3}{h_7{u}_1+h_8{v}_1+h_9}\\ v_2& =\frac{h_4{u}_1+h_5{v}_1+h_6}{h_7{u}_1+h_8{v}_1+h_9}\end{array}\text{\hspace{1em}(6)}$$
可以得到一点对的两个约束如下 (写成如此只要是为了和源码中的形式相对齐):
$$\{\begin{array}{r}-h_1{u}_1-h_2{v}_1-h_3+h_7{u}_1{u}_2+h_8{v}_1{u}_2+h_9{u}_2=0\\ h_4{u}_1+h_5{v}_1+h_6-h_7{v}_2{u}_1-h_8{v}_2{v}_1-h_9{v}_2=0\end{array}\text{\hspace{1em}(7)}$$
进而按照以上方式计算出八点对,组成如下矩阵求解:
$$\left[\begin{array}{ccccccccc}0& 0& 0& -u_1& -v_1& -1& u_1{v}_2& v_1{v}_2& v_2\\ u_1& v_1& 1& 0& 0& 0& -u_1{u}_2& -u_2{v}_1& -u_2\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right]\left[\begin{array}{c}{h}_1\\ h_2\\ h_3\\ h_4\\ h_5\\ h_6\\ h_7\\ h_8\\ h_9\end{array}\right]=0\text{\hspace{1em}(8)}$$
至于求解该方程的方式与上述求解F矩阵类似,此处就不再叙述.

根据单应矩阵H / 基础矩阵F 求解R,t

由于此篇幅较多,故单独置一章节讲解:一步步带你看懂orbslam2源码–单应矩阵/基础矩阵,求解R,t(四)

RANSAC随机采样一致性算法

(1)算法流程如下:

  而在orbslam2中,实际操作则是随机选择200组8点对进行求解H矩阵和F矩阵,选择其中$score$最高的H矩阵/F矩阵.

(2)score计算流程:

  根据orbslam2论文中所述,在上述得到了H矩阵之后,利用H矩阵,将P点分别投影到$camera1$和$camera2$中,分别在两帧图像中计算P点的重投影误差(即两点之间的距离),且该距离的平方必须小于阈值$T_M$才有效,并将所有匹配点的有效的重投影误差累加起来 (当然并不是直接将重投影误差直接相加,而是进行了标准化,后续源码实现环节将会进行讲解),即得到$score$,具体公式如下:

  其中,$d^2$为重投影误差(两点间距离的平方),$d_{cr}$ 和 $d_{rc}$分别对应将P点分别投影到$camera1$和$camera2$中的重投影误差,${\rho }_M(.)$对应这判断该点的重投影误差是否小于阈值,小于则有效,结果累加进$score$中,大于则代表无效,舍弃.
  相应的计算基础矩阵$F$的$score$,同样采用双向投影计算,不同的是:计算$p_2$点到直线$F_{21}\ast p_1$的距离的平方,如果读者留意到的话,会发现就是计算投影点到极线的距离.

(3)阈值$T_M$的选择:

  该阈值的选择主要依赖于卡方分布统计量 (即正态分布的平方的累加,累加个数即为自由度),显著性水平为$5\%$,在单应矩阵H中,自由度为2,对应的阈值$T_H=5.991$,在单应矩阵F中,自由度为1,对应的阈值$T_F=3.841$.如下图所示:

模型选择策略

  orbslam2中采用并行计算单应矩阵和本质矩阵,在算出两个矩阵对应的$score$之后,按照如下公式计算$R_H$
$$R_H=\frac{S_H}{S_H+S_F}$$
如果$R_H>0.4$,则选择采用单应矩阵H恢复相机位姿,否则使用基础矩阵F.这也说明了orbslam2作者更加倾向于使用单应矩阵进行初始化,单应矩阵对视差小的容忍度比基础矩阵更好,即更适合位移较小的情形.

---

源码分析环节

(1)Frame帧创建处理补充

  在讲解单目初始化之前,先补充下上节提取完ORB之后的一些处理,其中包括去畸变以及将特征点分配到对应网格中,分别对应以下两个函数.

UndistortKeyPoints();
AssignFeaturesToGrid();

我们先来看看去畸变函数,去畸变后的像素点存放于mvKeysUn向量之中,具体代码如下.

//将像素坐标进行去畸变,并存入mvKeysUn
void Frame::UndistortKeyPoints()
{
    if(mDistCoef.at<float>(0)==0.0)
    {
        mvKeysUn=mvKeys;
        return;
    }
    // Fill matrix with points
    cv::Mat mat(N,2,CV_32F);
    for(int i=0; i<N; i++)
    {
        mat.at<float>(i,0)=mvKeys[i].pt.x;
        mat.at<float>(i,1)=mvKeys[i].pt.y;
    }
    // Undistort points
    mat=mat.reshape(2);
    cv::undistortPoints(mat,mat,mK,mDistCoef,cv::Mat(),mK);
    mat=mat.reshape(1);

    // Fill undistorted keypoint vector
    mvKeysUn.resize(N);
    for(int i=0; i<N; i++)
    {
        cv::KeyPoint kp = mvKeys[i];
        kp.pt.x=mat.at<float>(i,0);
        kp.pt.y=mat.at<float>(i,1);
        mvKeysUn[i]=kp;
    }
}

  首先将mvKeys向量中存放的特征点坐标存入cv::Mat mat(N,2,CV_32F)矩阵之中,接着调用cv::undistortPoints(mat,mat,mK,mDistCoef,cv::Mat(),mK);实现去畸变.让我们来看看OpenCV库是怎么实现的吧.

在此源码中,大致流程总结如下:

  至于源码中为何要进行矩阵通道的改变,即先将矩阵转化为双通道,去畸变完成后又将矩阵转换为单通道.其实,此处可以进行此操作也可以不进行次操作,因为undistortPoints()函数的src如下图所示,既可以是N×2单通道,也可以是N×1双通道.去畸变后将其坐标,又从mat矩阵存入mvKeysUn向量中.

  矫正完成后的特征点,通过AssignFeaturesToGrid()函数,将其分配到对应的网格中,大致思路是将特征点的坐标转换为网格坐标,然后判断该坐标是否在网格坐标范围内,如果是,则存入对应的网格,否则抛弃该野点.实现代码如下:

//将特征点分配到对应的网格中
void Frame::AssignFeaturesToGrid()
{
    int nReserve = 0.5f*N/(FRAME_GRID_COLS*FRAME_GRID_ROWS);
    for(unsigned int i=0; i<FRAME_GRID_COLS;i++)
        for (unsigned int j=0; j<FRAME_GRID_ROWS;j++)
            mGrid[i][j].reserve(nReserve);

    for(int i=0;i<N;i++)
    {
        const cv::KeyPoint &kp = mvKeysUn[i];

        int nGridPosX, nGridPosY;
        if(PosInGrid(kp,nGridPosX,nGridPosY))//判断是否存在nGridPosX,nGridPosY
            mGrid[nGridPosX][nGridPosY].push_back(i);
    }
}

  到这里就正式完成了对一帧照片的处理(提取ORB特征点并进行相应的存储),接下来我们来讨论下如何进行单目初始化.
  我们先看下单目初始化的总体代码框架:

  让我们来看看这个函数里面是什么东西,点开一看,发现此处调用了一个重载过的括号运算符.

  最开始创建Tracking线程的时候,mpInitializer指针将会赋值为NULL,直到当前帧中的特征点数量>100并成功初始化时,才会执行下面语句进行赋值.因此,只会初始化一次.

mpInitializer =  new Initializer(mCurrentFrame,1.0,200);

关于单目初始化由于篇幅较长,就留到后文继续讲解了…

---

总结

1. 对极约束的原理,以及F矩阵的求解
2. 单应矩阵的原理,以及H矩阵的求解
3. RANSAC随机采样一致性算法,阈值选择原理
4. score计算方式,模型选择策略
5. 创建Frame时源码的部分补充

参考文献:

1. ORB-SLAM a Versatile and Accurate Monocular SLAM System
2. 高翔–视觉SLAM十四讲
3. 吴博-ORB-SLAM代码详细解读
4. 其他博主的文章:https://blog.csdn.net/hzwwpgmwy/article/details/83578694

PS:

1. 如果您觉得我的博客对您有所帮助，欢迎关注我的博客。此外，欢迎转载我的文章，但请注明出处链接。
2. 本博客仅代表个人观点,不一定完全正确,如有出错之处,也欢迎批评指正.
   

 
 
上一章节:一步步带你看懂orbslam2源码–orb特征点提取(二)
下一章节:一步步带你看懂orbslam2源码–单应矩阵/基础矩阵,求解R,t(四)