Array Shrinking（区间DP）codeforces Educational Codeforces Round 83 (Rated for Div. 2)

题目大意

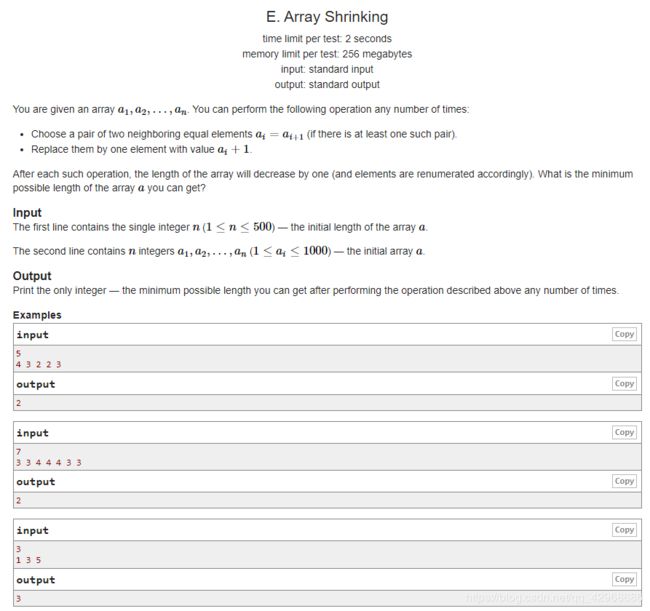
       给一个长度为$n(n<=500)$的数组，每次可以把相邻的两个相同元素$a_i$和$a_{i_{+}1}$合并为$a_i+1$，问数组在若干次操作后可以取得的最小长度为多少？

分析思路

       关于这道题目网上已经有了很多题解博客，但是基本上都没有把分析思路写的很详细，于是我写下这篇博客，记录一下自己的分析过程。
       这个题目的数据范围为$(n<=500)$，所以可以考虑用区间DP搞一下。设$dp[i][j]$为对应区间$[i,j]$能够经过合并取得的最短长度。首先考虑对任一区间$[i,j]$来说，要么最终可以合并为1个元素，要么不能合并为1个元素。如果不能合并为1个元素，那么必然存在一个最优分割点$k$使得$$dp[i][j]=dp[i][k]+dp[k+1][j]$$如果能合并为同一个元素，那么必然存在最优分割点$k$使得$$dp[i][j]=dp[i][k]+dp[k+1][j]+1$$而取到这个最优分割点的条件便是此分割点两侧区间均能合并为同一个值，且它们相等。因此，区间$[i,j]$的状态转移方程为$$dp[i][j]=\underset{k=i}{\overset{j-1}{\min }}\{dp[i][k]+dp[k+1][j]-(dp[i][k]==1\&\&dp[k+1][j]==1\&\&m[i][k]==m[k+1][j])\}$$其中，$m[i][j]$表示区间$[i,j]$最终合并为同一个元素的元素值。

AC代码

#include
using namespace std;
const int maxn = 507;
const int MAXINT = 6000000;
int n, dp[maxn][maxn], m[maxn][maxn], a[maxn];
void solve(){
	int i, j, k, len;
	//初始化 
	for(i=1;i<=n;++i){
		for(j=1;j<=n;++j){
			dp[i][j] = MAXINT;
		}
		dp[i][i] = 1;
		m[i][i] = a[i];
	}
	
	for(len=2;len<=n;++len){
		for(i=1;i<=n-len+1;++i){
			j = i + len - 1;
			for(k=i;k<=j-1;++k){
				dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j]);
				if(dp[i][k] == 1 && dp[k+1][j] == 1 && m[i][k] == m[k+1][j]){ //如果可以合并为一个元素 
					dp[i][j] = 1;
					m[i][j] = m[i][k] + 1; 
				}
			}
		}
	}
	cout<>n;
	for(i=1;i<=n;++i) cin>>a[i];
	solve();
	return 0;
}