codeforces #628 div2 F题（DFS树/找环/独立集）

题目链接

题目大意

       输入一个由$n$个顶点和$m$条边组成的无向图，找一个长度$\ge \sqrt{n}$的环或者是顶点数为$\sqrt{n}$的独立集（独立集中任意两个点没有直接边）。

分析过程

       此题用$DFS$树求解，所谓$DFS$树就是将图进行$DFS$遍历之后导出的树，如下图所示。（粗线为树边，浅线为非树边）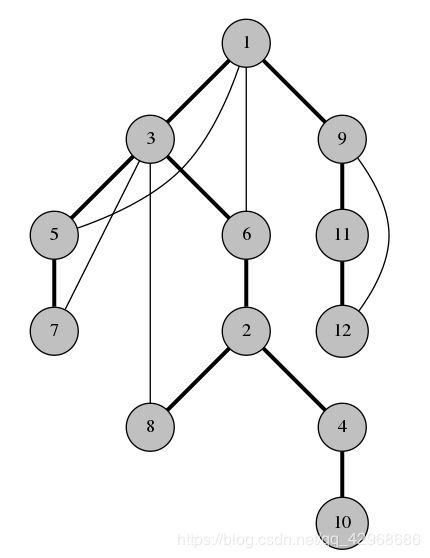
       $DFS$树有一个重要的性质，不在同一颗子树上的两点之间没有边（非树边只有可能是在同一条树链上），这个用反证法的思路和$DFS$的性质能够容易看出。
       $DFS$树找出的环不一定是最大环也不一定是最小环。比如下面这组数据。（找最小环需要用$Floyd$）

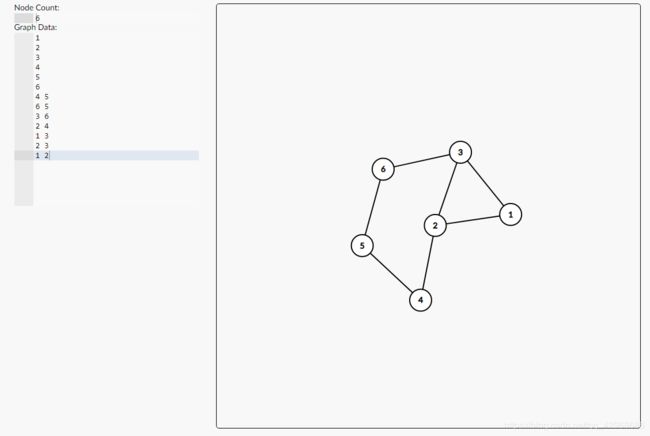
• 这组数据的最大环是124563最外面这个环，$DFS$树中找不到这个环。
• 回到这道题目上面来，在$DFS$树上遇到环时判断对应非树边的两个端点差$dep[u]-dep[v]+1>=d$是否成立，如果成立则直接输出这个环。（$dfs$的过程中开堆栈存一下同条树链上已经访问的历史节点）
• 否则，$DFS$树同一条树链上的高度差为$d-1$的顶点之间必然没有环，因此可以用$\mathrm{m}\mathrm{o}\mathrm{d}(d-1)$的方式划分等价类，所有同余的顶点两两之间必然没有边，即可以组成独立集。由鸽巢原理，一共有$n$个顶点，划分成$d-1$个等价类，必然至少有一个等价类中的元素个数$\ge$d。

这道题也是DFS树留个坑。

AC代码

#include
using namespace std;
const int maxn = 2e5 + 100;
typedef long long ll;
int n, m, d, flag, dep[maxn];
vector<int> G[maxn];
stack<int> s;
void dfs(int cur, int par){
	dep[cur] = dep[par] + 1;
	s.push(cur);
	for(auto temp:G[cur]){
		if(temp == par) continue;
		if(!dep[temp]){
			dfs(temp, cur);
			if(flag) return;
			s.pop();
		}else{
			if(dep[cur] - dep[temp] >= d - 1){ //找到符合条件的环 
				cout<<2<<'\n';
				flag = 1;
				cout<<dep[cur] - dep[temp] + 1<<'\n'<<s.top();
				s.pop();
				while(!s.empty()){
					cout<<' '<<s.top();
					if(s.top() == temp) return;
					s.pop();
				}		
			}
		}
	}
}
void solve(){
	int cnt[maxn];
	memset(cnt, 0, sizeof(cnt));
	d = sqrt(n + 0.5);
	if(n > d * d) ++d;
	dfs(1, 0);
	if(!flag){ //存在独立集
		cout<<1<<'\n';
		int maxi = 0, p, c = 0; 
		for(int i=1;i<=n;++i){
			cnt[dep[i]%(d-1)]++;
			if(cnt[dep[i]%(d-1)] > maxi){
				maxi = cnt[dep[i]%(d-1)];
				p = dep[i]%(d-1);
			}
		}
		for(int i=1;i<=n;++i){
			if(dep[i] % (d - 1) == p){
				if(c) cout<<' ';
				cout<<i;
				++c;
				if(c >= d) break;
			}
		}
	}
}
int main(){
	int t, i, j, u, v;
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(i=1;i<=m;++i){
		cin>>u>>v;	
		G[u].push_back(v);
		G[v].push_back(u);
	}
	solve();
	return 0;
}