Python数据结构和算法(六)：哈希算法(hash)的六大应用以及哈希一致性的介绍和实现

前文

  说到哈希算法大家应该都不陌生，但系数它的应用范围，大多数人只能答出少部分，比如用于加密，比如用于散列表，比如MySQL的哈希索引，但再多可能就不清楚了。实际上总结起来有以下7点：加密、唯一标识、数据校验、散列函数、负载均衡、数据分片、哈希一致性的分布式存储。前面6个会简单地讲过，重点记录下第七点，而哈希一致性也是面试时最容易考察的知识点。
  本文是总结极客时间的《数据结构和算法之美》，若要更具体的内容，可以去订阅来看。

哈希算法定义和特征

  定义：将一段任意的二进制串映射成固定长度的二进制串。
  特征：

• 不可逆：即加密后无法逆转回来
• 对数据敏感：即使改1个字符，生成的串也完全不同
• 散列冲突小：无法避免散列冲突，根据“鸽巢原理”，假如10个鸽巢要放入11个鸽子，则必然有巢要放置两个。因为哈希算法是映射成固定长度的二进制串，比如MD5是映射成128位，即2¹²⁸，那只要放入的value多如2¹²⁸+1，那就必然出现散列冲突
• 执行效率要高效：表示这个映射过程要尽可能的快

哈希算法应用

安全加密

  由于不可逆的特点，哈希算法非常适合用于数据加密，常用加密算法：MD5（MD5 Message-Digest Algorithm，MD5 消息摘要算法）和 SHA（Secure Hash Algorithm，安全散列算法）。因为这些算法的不可逆，所以用于安全加密是非常合适的。比如MD5是加密成128bit的二进制串，比如SHA256是加密成256bit的二进制串，而根据鸽巢原理，加密长度越长的二进制串，则越不容易被破解，但同时执行效率就越低。所以速度与安全二者不可兼得，当然后续可能能发明二者兼具的加密算法。
  为了防止加密算法被破解，在开发web平台的时候常常会加入salt(盐，一串随机的二进制数)来配合加密算法来加密。

散列函数

  散列函数是散列表的重要依赖，比如Python的字典，就通过__hash__这个魔法方法来构建散列函数将值转为key。所以哈希算法在散列函数里更看重的是散列冲突小、执行效率高效这两个特点，而对于是否可逆，则相对不重要。

唯一标识

  常常用hash来构建唯一标识，比如一组规模很大图片里如何快速查找到1张图片？可以通过将每张图片通过hash构建成1个hash值作为key，取其文件路径作为value，然后存储到散列表里。因为每张图片都是一个二进制串，所以可取前后各100位bit通过hash作为key。
  所以当要查找某张图片的时候，先构建其hash的key，然后在散列表里查找即可。

数据校验

  这点则是利用到哈希算法的数据敏感这个特点，也就是用于校验数据是否被修改，因为只要小小的修改，那么哈希出来的数据也是完全不同的！所以常常可以用来校验文件的是否改变，比如文件在传输过程中如果丢失数据包或者被篡改，通过hash值就可以很容易对比得到结果。
  在linux里就有md5sum这么一个函数，可以查看任意文件的MD5值，所以如果在linux传输时，可以比对前后两个md5的值是否一致来确认文件是否有被改动。

负载均衡

  通过哈希可以实现一个会话粘滞(session sticky)的负载均衡算法，即客户端和服务端即使是多对多的情况下，仍保证同一个客户端仅对应同一台服务器。
  可以利用哈希算法将客户端的ip哈希成一个数值，然后对服务器大小进行取模运算，得到的结果就是要发往的位置，这样就能保证发往的服务端永远都是同一台机器。所以在nginx上我们可以指定ip_hash来实现：

upstream bakend {  
    ip_hash;  
    server 192.168.0.1:88;  
    server 192.168.0.2:80;  
} 

数据分片

  数据分片的做法和负载均衡差不多，不过概念不同罢了。两个例子说明。

统计关键词次数

  要统计一份1TB的文件里用户关键词的次数，在单台机上又无法计算(内存不够，再者太耗时)，那此时就要将文件进行分片，到n台机上分别进行统计，最后汇整同样的关键词数目。那该如何操作呢？很简单，将每台机计算的关键词进行哈希运算，然后对n台机取模，发往对应的机器即可。这样相同关键词的都会只发往一台机子上。

快速找出图片是否存在图库

  如果有1亿张图片该如何存储？而又如何快速判断需要的图片是否存在呢？如果用散列表构建，那得需要多大的内存才能存的下，很明显也不切实际。所以这里利用数据分片，将1亿张图片分开存储到多台机器上。那具体如何操作？
  可以根据上述的唯一标识，通过取前后各100位来构造散列表的key，文件路径为散列表的val，然后在将key对n台服务器进行取模，然后分配到对应的服务器上构造对应的散列表。同理，如果要查找一张图片是否存在图库，那就对这张图片先hash，然后取模后去对应的服务器再通过散列表就能快速的确定图片是否存在。
  那如何确认n的值呢？假设我们通过 MD5 来计算哈希值，那长度就是 128 比特，也就是 16 字节。文件路径长度的上限是 256 字节，我们可以假设平均长度是 128 字节。如果我们用链表法来解决冲突，那还需要存储指针，指针只占用 8 字节。所以，散列表中每个数据单元就占用 152 字节（这里只是估算，并不准确）。假设一台机器的内存大小为 2GB，散列表的装载因子为 0.75，那一台机器可以给大约 1000 万（2GB*0.75/152）张图片构建散列表。所以，如果要对 1 亿张图片构建索引，需要大约十几台机器。

哈希一致性

哈希一致性的定义和使用

  哈希一致性是哈希算法里最容易被考到的用法，因为在分布式存储里应用广泛。并且其解决了数据分片、负载均衡的一大难题：那就是这两个都依赖于对服务器列表大小n取模来判断key的归属，但是如果n变化，则原来key的存放位置就全部都变更。比如我们再数据库MySQL来进行分布式存储，如果用4个实例存放1亿条数据，根据每条数据的主键来hash得到其要分配的机器，那么当4个实例挂了1个实例，此时要基于3个实例来分配，那该如何处理才能使1亿条数据不需要重新分配key的取模运算？当数据增加过多，4个实例需要增加1个实例到5个实例，又该如何处理？
  哈希一致性就是为了解决这样的分布式缓存而存在，其概念本质是：定义数据的哈希值范围[0,MAX]，然后基于这个范围将数据分为m个小空间，然后将k台机器放置于上面(m远大于k)，这样每台机器负责m/k个空间的数据(也可以理解为将数据存放在哈希值范围区间，然后每个机器管理两台机器之间的数据)，当有机器上线或者下线，那么就改变其相邻的数据存储即可，而不用迁移整个数据！
  为了解释一次性哈希，所以引入了哈希环，这里借用下小灰的图，参考链接：https://mp.weixin.qq.com/s/yimfkNYF_tIJJqUIzV7TFA，在如下的图中，整个环可以看成是哈希值范围[0,MAX]，而环上的每一个点用于存放数据，这个点可大到环只能存放60个数据，也能小到能存放2³² 个数据，由我们自定义。下图的node即是机器，所以4个node间的区域就是其所存放的数据，更准确的说从环顺时针开始遍历，从1个机器到下一个机器之间的数据都是属于下一个机器。

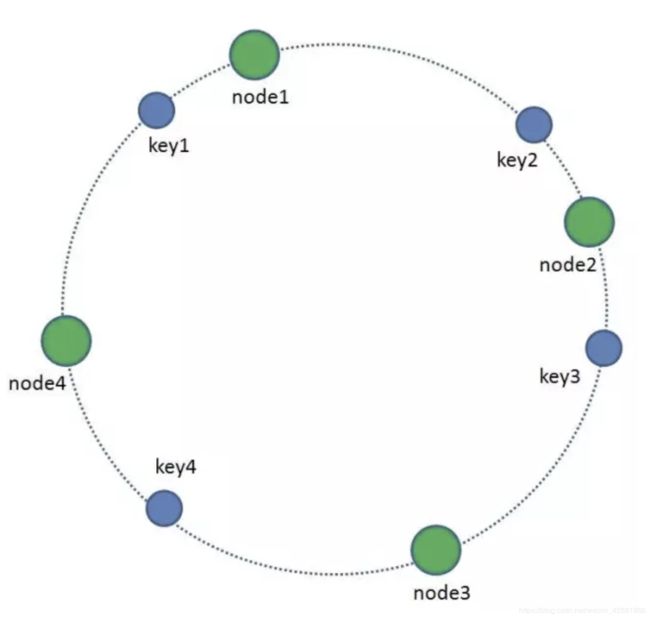
  了解了定义后，来分析上下线机器造成的影响。如果node2和node3之间上线node5(如下)，那么原属于node3的key3要迁移到node5，也就是只造成属于node3的部分key要进行迁移；如果不上线node5，同时下线node3，那就是把原属于node3的key3迁移到node4即可。这就能通过简单地迁移部分机器的数据实现快速的分布式管理！

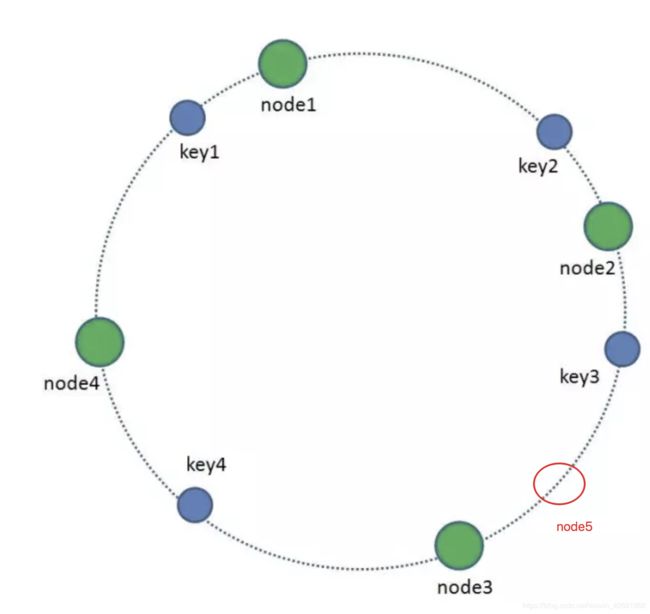
  要注意的是，如果哈希后的数据全部存放到一个区域，而导致这个区域的数据全部归属于一台机器，那就会完全退化成单机器部署，利用不到分布式缓存。为了解决这个问题，引入了虚拟节点这个概念。也就是将环中的每个节点都转换成多个虚拟节点，这里的多个由用户自定义，比如如果机器较少的话，那虚拟节点就可以多点；机器多的话，虚拟节点就能少点。假设定义成4个虚拟节点，那原本只有4个node的分布式缓存就变成了16个。而这个虚拟节点的得到完全可以通过hash算法来得到，命名可以标记为node1#1，node1#2，node1#3，node1#4这样。由此便能分散存储key。

哈希一致性来定义分布式存储MySQL表

  所以此时回到开头的那个问题，1亿条数据存放分布式MySQL，该如何存储才不会因为机器的上下线导致要重新迁移数据。那通过哈希一致性就能很简单地解决这个问题，我们先定义4个实例用于存储，将4个实例所在的ip通过设置3个虚拟节点分散成12个节点存于环中，然后将1亿条数据的主键值(可以自定义uuid)依次hash后存放到环中。

• 查找：每次将要查找的数据hash后然后查看环中离他最近的节点(在代码实现时，即有序数组中离它最近并比它大的那个数)
• 删除：先hash查找到，然后删除所在的key，删除对应机器上MySQL的值
• 增加：hash后存放，然后找到对应的机器，再到其上MySQL增加
• 改值：先hash查找到，然后更改对应机器上MySQL的值。

哈希一致性的实现

  哈希一致性的实现借鉴这篇：https://techspot.zzzeek.org/2012/07/07/the-absolutely-simplest-consistent-hashing-example/。利用有序数组来二分法快速找到对应的key，利用散列表来存储nodename和node的对应关系，从而快速找到对应的值所存储的区域！代码如下：

import hashlib
import bisect


class ConsistentHashRing:
    def __init__(self,virtual_nums=4):
        self._virtual_nums = virtual_nums #默认为4个虚拟节点
        self._nodes = {}  #_nodes存放所有节点，key为虚拟节点的hash值，val为真实ip
        self._keys = []  #存放所有虚拟节点的hash值，为有序数组，用于快速查找hash的key

    def _hash(self,key): #用md5来实现hash值
        md5_str = hashlib.md5(key.encode("utf8")).hexdigest()
        return int(md5_str,16) #返回2进制数

    def _repl_iterator(self, nodename):
        """根据编号和nodename，给每个虚拟节点取名后赋值hash"""

        return (self._hash("%s:%s" % (nodename, i)) for i in range(self._virtual_nums))

    def __setitem__(self, nodename, node): #nodename为自定义标识名字，比如node1, node:192.168.4.1
        for hash_ in self._repl_iterator(nodename):
            if hash_ in self._nodes:
                raise ValueError("Node name %r is "
                            "already present" % nodename)
            self._nodes[hash_] = node
            bisect.insort(self._keys,hash_) #二分法插入

    def __delitem__(self, nodename): #删除要同时删除_nodes和_keys的值
        for hash_ in self._repl_iterator(nodename):
            del self._nodes[hash_]
            index = bisect.bisect_left(self._keys,hash_)
            del self._keys[index]

    def __getitem__(self, key): #通过二分法快速查找
        hash_ = self._hash(key)
        start = bisect.bisect(self._keys,hash_) #返回这个key应该插入的位置，如果是最右边，则属于第0个节点
        if start == len(self._keys)-1:
            start = 0
        return self._nodes[self._keys[start]]

consistent_hash_ring = ConsistentHashRing()
consistent_hash_ring["node1"] = "192.168.4.1"
consistent_hash_ring["node2"] = "192.168.4.2"
val1 = consistent_hash_ring["10_hash"] #加入key取名为主键+_hash，那第10个主键的key就是 10_hash
val2 = consistent_hash_ring["20_hash"]
print("哈希环存放的键值对为：",consistent_hash_ring._nodes)
print("哈希环当前所有的虚拟节点集合为：",consistent_hash_ring._keys)
print("10_hash存放的机器位于：",val1)
print("20_hash存放的机器位于：",val2)

结果为：

哈希环存放的键值对为： {127097526815233298582794356773614554855: '192.168.4.1', 82085472036366309913032597666696857451: '192.168.4.1', 339427956960730678991081772292544573879: '192.168.4.1', 297393281242721132585495680199299683151: '192.168.4.1', 234270789901673706184978332503042424895: '192.168.4.2', 30800198962622170283128992779263460808: '192.168.4.2', 285952547974116111993108643362078034539: '192.168.4.2', 152869870438375595209842928583682618037: '192.168.4.2'}
哈希环当前所有的虚拟节点集合为： [30800198962622170283128992779263460808, 82085472036366309913032597666696857451, 127097526815233298582794356773614554855, 152869870438375595209842928583682618037, 234270789901673706184978332503042424895, 285952547974116111993108643362078034539, 297393281242721132585495680199299683151, 339427956960730678991081772292544573879]
10_hash存放的机器位于： 192.168.4.1
20_hash存放的机器位于： 192.168.4.2

总结

  哈希一致性的实现也是颇为简单，甚至可以通过红黑树、跳表这种数据结构来代替有序数组，致使效率更快。这次就总结到这~