深度学习：一文解决卷积，池化，反卷积的维度问题（包含一些工程思考）

一文解决卷积，池化，反卷积的维度问题

1. 背景

其实这个之前LZ对这个关注度不是很高，像tensorflow，选择‘valid’和‘same’也就可以了，但是对于caffe不可以。并且在海思芯片使用的caffe1.0，据前端同事说很多骚操作在前端都是不支持的，哭泣中，即使在重训的时候可以重新写C，来添加层，在NNIE推断结果还是不行。。。

按理说华为内部应该是有一波大神来构建对应的代码来支持比较新的网络层的，这应该也算是一种技术壁垒吧，纯属猜测。

还有量化误差的问题，这个真的也是无力吐槽，据说9月份就会出tensorflow和pytorch定点化重训的包，消息待确认，效果呢也待确认，坑还是蛮多的。

回归重点，本篇博客主要是参考这篇paper：A guide to convolution arithmetic for deep learning，篇幅不是很长，30页左右，而且包含很多图，LZ查了很多博客都是用的这篇paper的截图，读起来也很简单，可以作为基础知识归纳

2. 卷积、池化、反卷积（转置卷积）

特别基础的什么是卷积，LZ就不再赘述了，主要关注卷积和转置卷积的维度关系：

1. 卷积

对于任意的输入（w=h=i）, padding: p, 核的大小：k，步长stride = s，我们可以得到输出的尺寸为：

$\lfloor .\rfloor$是向下取整，看到有博客向上和向下取整还是反的

2. 池化

池化层不太涉及到padding部分，如果要保证对应的输入输出大小，同样进行padding就可以了

假设，我们不考虑padding，那么对于任意的i，k和s，输出的维度为：

3. 反卷积（转置卷积）

a. 为什么叫反卷积（或者转置卷积）？

主要参考的https://www.zhihu.com/question/43609045

总结说来，就是正常情况下，网络做关于卷积的运算有两个，一个是进行前向推断的时候，做的卷积操作，另一个是在反向传播的时候，需要计算对应的导数，这是两个相反的过程.

假设现在有一个4x4的输入，假设我们核的大小为3x3，stride=1，pad=0，如下图：

输入矩阵可展开为16维向量，记作$x$
输出矩阵可展开为4维向量，记作$y$
卷积运算可表示为 $y=Cx$
上面是网络卷积正向传播的过程，那么反向传播呢？直接截图了，来自参考文献2

所以反卷积其实就是正向传播时左乘$C^T$,而反向时左乘$(C^T{)}^T=C$

所以反卷积（逆卷积）是针对网络做卷积这个过程来取名的，而转置卷积，即使是从数学推导上来取名的，这个感觉都可以，理解是啥就行了

b. 维度问题

看图来理解一下什么是转置卷积：

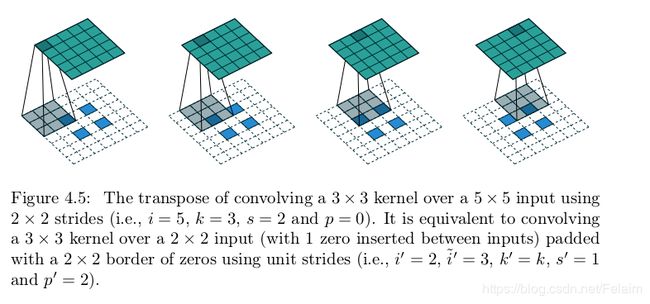
上述图是stirde不为1的情况，通常使用转置卷积是为了扩大维度，这样stride一般是大于1的，那么在卷积过程中，我们可以看到如果输入是2x2,为了扩充维度，会进行补零的一个操作。

在看一个例子：

通过a中的解释，其实可以知道卷积和转置卷积是两个相反的过程，那么换句话说，原来卷积的输入变成了反卷积的输出，维度也是这样，但是在正向计算中，我们是有向下取整操作的，所以还要分情况考虑：

• 情况一
  
• 情况二

好啦，维度问题记不住，下次查下公式也就可以啦！

3. 工程上的一些思考

其实涉及到tensorflow一个resize操作代替，因为caffe里面没有resize层，所以上采样的时候，也就考虑到了转置卷积，其中有两种方式，第一种：直接把转置卷积中的权重和偏置学出来，当正常卷积的方式，第二中其实就是当成一个双线性插值的操作

1. 在caffe源码 include/caffe/filler.hpp有一段 ：

@brief Fills a Blob with coefficients for bilinear interpolation.
A common use case is with the DeconvolutionLayer acting as upsampling.
You can upsample a feature map with shape of (B, C, H, W) by any integer factor
using the following proto.
\code
layer {
  name: "upsample", type: "Deconvolution"
  bottom: "{{bottom_name}}" top: "{{top_name}}"
  convolution_param {
    kernel_size: {{2 * factor - factor % 2}} stride: {{factor}}
    num_output: {{C}} group: {{C}}
    pad: {{ceil((factor - 1) / 2.)}}
    weight_filler: { type: "bilinear" } bias_term: false
  }
  param { lr_mult: 0 decay_mult: 0 }
}
\endcode
Please use this by replacing `{{}}` with your values. By specifying
`num_output: {{C}} group: {{C}}`, it behaves as
channel-wise convolution. The filter shape of this deconvolution layer will be
(C, 1, K, K) where K is `kernel_size`, and this filler will set a (K, K)
interpolation kernel for every channel of the filter identically. The resulting
shape of the top feature map will be (B, C, factor * H, factor * W).
Note that the learning rate and the
weight decay are set to 0 in order to keep coefficient values of bilinear
interpolation unchanged during training. If you apply this to an image, this
operation is equivalent to the following call in Python with Scikit.Image.
\code{.py}
out = skimage.transform.rescale(img, factor, mode='constant', cval=0)
\endcode
 */

2. 怎么书写对应的pycaffe呢？

 conv_param = {
        'kernel_size': 3,
        'stride': 2,
        'num_output': 3,
        'pad': 1,
        'weight_filler': dict(type="bilinear"),
        'bias_term': False
    }

    coarse_resize = caffe.layers.Deconvolution(coarse_out, convolution_param=conv_param, param=[dict(lr_mult=0)])

以为这样就大功告成了吗？

3. 棋盘格效应

当factor比较小，确实可以利用反卷积进行插值操作，但是当factor比较大的时候，就会出现比较明显的棋盘格效应。。。比较好的代替方式是采用上采样+卷积，但是，这就违背了LZ一开始使用反卷积的意愿，所以，恩，生活总是给你希望，然后告诉你不行，然后再给你希望，周末愉快！

4. 参考文献

1. A guide to convolution arithmetic for deep learning

2. 转置卷积理解https://www.zhihu.com/question/43609045

3. caffe 转置卷积源码https://github.com/BVLC/caffe/commit/41df4cdce942c22f0d89ad8b0990d3ee7bd9cf31