【数据库系统】关系代数之基本运算、附加运算、扩展操作
数据库系统学习第七篇：关系代数之基本运算、附加运算、扩展操作。参考书籍：数据库系统概念。
文章目录
- 基本运算
- 选择运算
- 投影运算
- 并运算
- 差运算
- 笛卡尔积
- 更名运算
- 附加运算
- 交运算
- 自然连接（Natural Join）
- 除法
- 赋值
- 扩展操作
- 广义投影
- 聚集函数
- 外连接
基本运算
基本运算有6种，如下所示：
选择运算
选择运算的目的是 选出满足给定谓词的元组，表示如下：
选择运算可以有如下规则：
- 允许在谓词中 > = < 等 符号 进行比较，如找出工资大于90000美元的所有元组。
.
2.允许 用 ^（and）、 ∨（or）、¬（not）将谓词组成更大的谓词，如为了找到物理系中工资额大于90 000美元的教师，我们需要书写:
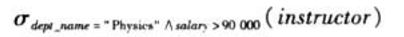
3.允许谓词中出现对属性的比较，如找到那些系名和楼名相同的系：
投影运算
投影运算就是对关系的某些性质进行选择，并产生新的关系，由于关系是集合，所以去掉重复的元组，保留一个就行。但是实际情况查询的时候，如果没有加distinct关键字，允许结果出现重复的元组。投影用大写字母pi（π） 表示。举例如下，选取instructor的 id ，name ，以及salary属性：
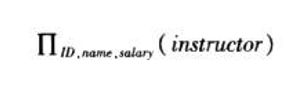
并运算
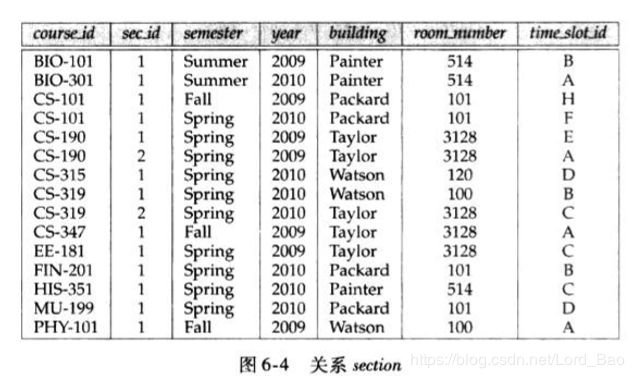
并运算可以将两次运算的结果 归并为一个更大的结果。如为了找到2009年秋季学期开设的所有课程和2010年春季学期开设的课程，我们可以采取如下的方式：
并运算要注意满足两个原则，以关系 r 和 关系s 进行r U s运算举例：
- 关系r和s必须是同元的，即它们的属性数目必须相同。
- 对所有的i,r的第i个属性的域必须和s的第i个属性的域相同。
后面的差运算 和 交运算 同样满足这两个原则，就不再赘述。
差运算
见名知义， r - s 可以如下图来理解，橘色那块就是r-s：
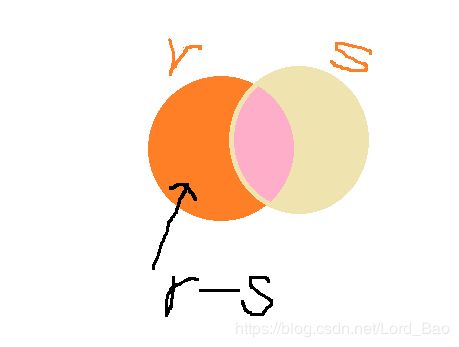
笛卡尔积
笛卡尔积没什么多说的，简单记住笛卡尔积可能会产生大量的无效元组，假设 计算前 关系 r 的元组有 m 个 ，关系s的元组有n个，那么 r x s 的元组 有 mn个。与笛卡尔积对应的有自然连接 及 外连接运算，根据实际情况选择采用笛卡尔积 、自然连接、外连接这三种运算。
更名运算
更名运算大致可以分为两种，一是对关系自己的更名，一是对关系的属性进行更名。
1.关系更名：下图表示将名字x赋给关系表达式E：
2.关系的属性更名：下图表示依次将A1，A2…An的名字赋给关系表达式E的各个属性，并将x赋给E：
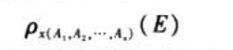
附加运算
基本关系代数运算针对某些计算时，可能显得比较冗长，为了便于表达 和 方便他人理解，所以给出了附加运算，附加运算可以分为4种：
交运算
交运算比较简单，注意保证 关系 r 和 s 是相容的（即满足上文并运算提到的两个原则）就行：
交运算可以由基本表达式表示为：
自然连接（Natural Join）
直接看下图，再解释：
如果关系模式 R 和 S 有相同的属性，那么在关系r和s进行笛卡尔积之后，就对这些相同的属性进行选择，然后再对所有的属性（重复的属性只取一次）进行投影。
与笛卡尔积很大的不同就是 ，自然连接的属性数目是小于或等于笛卡尔积计算后的属性数目的。
但是我们在实操时，只需找到两个关系相同的属性，一一比对就行，不用先进行笛卡尔积那样麻烦，例子
注意当关系 r 和 s 没有相同的属性时，也就是上文中
没有这个选择条件加以限制，也就是说此时自然连接等同于笛卡尔积。
除法
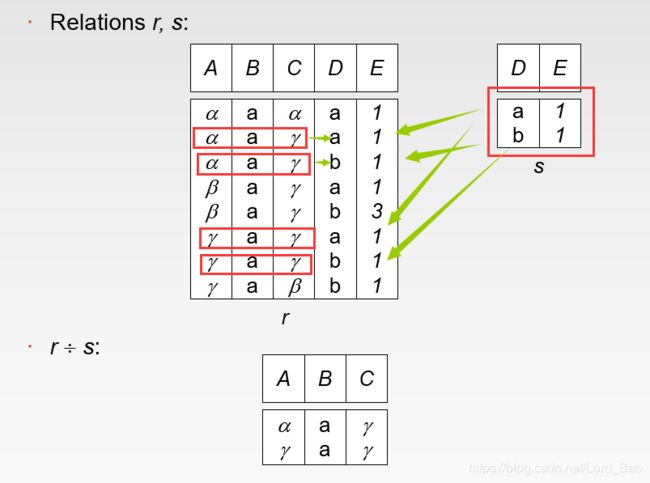
除法其实也是个找相同的问题，不过是尾部找相同的问题，先贴图
其中1是说明，除的关系模式的属性 必须是 被除的关系模式的一部分，并且是最后的一部分。（如果不是最后的一部分，自己手动移到最后的一部分即可）
其中2 中的任意符号，是除法的精要所在。它指明 r ÷s中 的元组必须满足如下条件：如果某元组是πR-S（r）中的元组，必须与任意的s中的元组结合起来的结果是r的元组 。可能这里解释不太直观，如下图所示：
赋值
赋值简单理解为就是为将关系表达式赋值给临时变量即可。如下：
扩展操作
扩展操作其实就是对前面的已经提到的关系表达式进行扩展 ，以扩大关系运算的适用范围。扩展操作包括下面三个方面：
广义投影
允许投影列表出现算数表达式，算数表达式通常涉及到一些常量 和 属性。
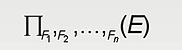
例如，我想知道每个导师ID name dept_name以及每个月的月薪时，就要对salary 除以12 如下所示：
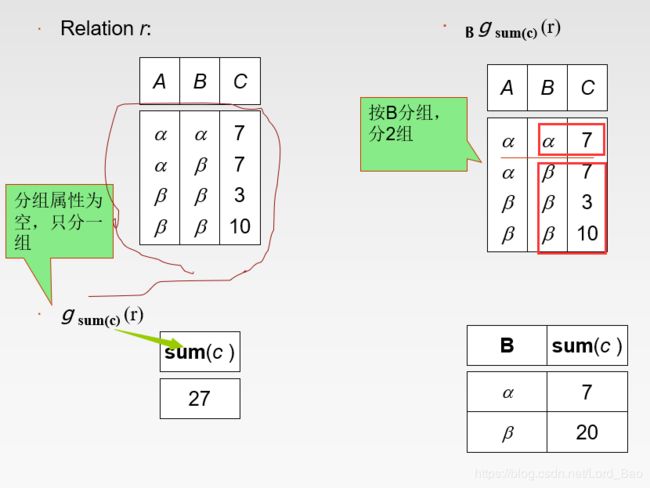
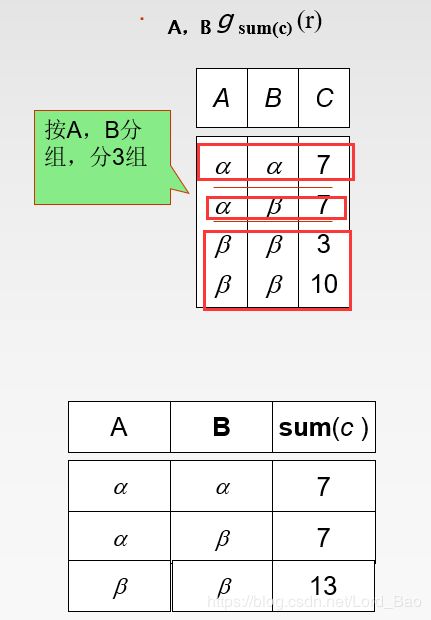
聚集函数
先记住G1，G2…Gn是分组条件 ，F1、F2…Fn是聚集函数 ，A1，A2，An是E中的属性。分组条件 和 聚集函数都要出现在结果中。
聚集函数满足如下条件：
- 同一组的所有元组在G1，G2，…Gn上的值是相同的。
- 不同组的元组针对 G1，G2…Gn的取值序列是不同的。
特别地，当分组条件不存在时，默认分为一组.。
举例说明：
外连接
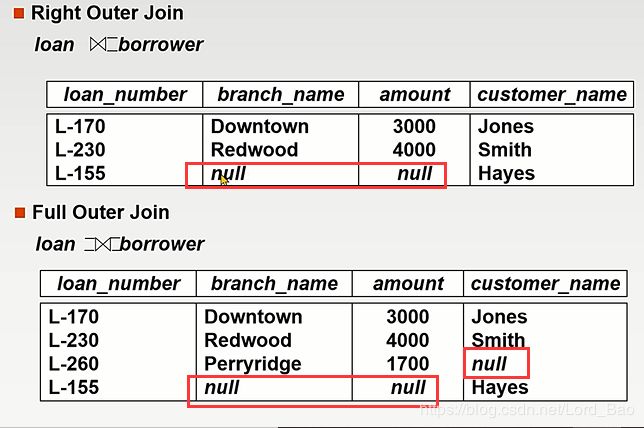
笛卡尔积会产生大量的无效元组，自然连接会丢失部分信息，那么外连接就是二者的折中方案。外连接分为左外连接，右外连接，全外连接。
以左外连接为例，它的意思是 r 和 s 进行自然连接产生新结果p以后，对于r未在p中出现的元组,则将该元组后面将s中与r未重复的属性均赋值为null，并添加到p中。这里可能不是解释得很清楚，看图：
与此相关的右外连接 和 全外连接：
写完收工！