《Few-Shot Learning with Graph Neural Networks》——少样本学习与图神经网络

一、简介

关于 Few-shot Learning（小样本学习），详细 可参考综述【1】，本文为叙述方便，现简要概括如下：

• 所谓 Few-shot Learning 就是小样本学习，直观的解释就是样本比较少的机器学习，【1】中指出它要解决的问题是：

机器学习模型在学习了一定类别的大量数据后，对于新的类别，只需要少量的样本就能快速学习。

• Few-shot Learning 是 Meta-learning（元学习） 在监督学习领域上的一个应用。其训练过程大致是这样的：

Few-shot 的训练集中包含了很多的类别，每个类别中有多个样本。在训练阶段，所使用的训练数据由两部分组成：第一部分为 support set，它是由训练集中随机抽取 C 个类别，每个类别 K 个样本（总共C * K 个数据）构成的；第二部分称为 test set ，它是从刚才抽取的 C 个分类的剩余数据中抽取一批测试样本作为模型的预测对象。这两部分数据合成为一个训练数据（task data），训练的目标就是要求模型能从 C*K 个数据中分辨出这 C 个类别，这样的任务被称为 C-way K-shot 问题。它的“有监督”体现在其 Loss 是构建在 test set 的预测分类与其对应 ground-truth 之间的差别上。

• Few-shot Learning 模型大致可分为三类：Mode Based，Metric Based 和 Optimization Based，如图1，在此，我就不做具体解释了，可参【1】
  
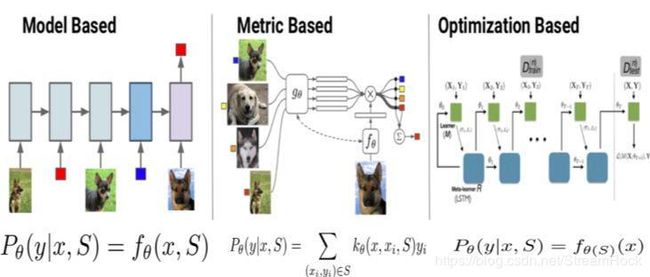
  图1、【1】中所述的三种 Few-shot Learning 模型

本博文是对【2】的解读，【2】采用的模型不同于上述三种，它将 Graph Neural Networks（图神经网络，GNN）应用到 Few-shot Learning 中：它将训练数据中每一幅 Image 映射为 Graph 上的一个 Vertex（顶点），通过训练，得到 Graph 中 Vertex 之间的 Adjacency Matrix，并利用它进行分类推断。
关于 GNN（图神经网络，Graph Neural Networks）可以参考【3】，为了叙述方便，简要介绍如下：

GNN 是对非欧空间（Non-Euclidean Space）中适合用 Graph 表达的数据，进行表达学习（Representation Learning）的神经网络模型。我们一般进行深度学习的数据，比如：Image、Text、Video 等，都是欧氏空间（Euclidean Space）中数据，比如Image，就可以看成是规则网格（regular grid）上的点构成的数据，在其上应用CNN（卷积网络），可获得数据后面隐藏的表达（Latent Representation），而一般的 Graph 结构，无法直接应用CNN，需要特殊的图卷积操作，才能得到其背后隐藏的图结构，如图2：

图2、2D 卷积 与 图卷积

GNN图网络是对图的学习，它不同与数据本身的学习，是对数据集所体现出来的图结构表达的学习，其概念要比普通的机器学习要间接一些，也要复杂和难懂一些。为了搞明白GNN图网络的思想，我特地找来 GNN 的一个应用实例——【2】，作为 GNN 学习的范例。

二、代码实现过程分析

图神经网络的概念比一般网络要间接，仅通读【2】并不能很好地把握文章的思想精华，结合其代码实现会有助于文章概念的理解。我在GitHub上找到一个基于 Pytorch 的实现【4】，以下将结合这份代码，来研究 GNN 是如何进行 Few-shot Learning 的。

2.1 数据的准备

先看代码，完整的代码请参考【4】，现摘抄部分代码如下：

class self_DataLoader(Dataset):
    def __init__(self, root, train=True, dataset='cifar100', seed=1, nway=5):
        super(self_DataLoader, self).__init__()

        self.seed = seed
        self.nway = nway
        self.num_labels = 100
        self.input_channels = 3
        self.size = 32

        self.transform = tv.transforms.Compose([
            tv.transforms.ToTensor(),
            tv.transforms.Normalize([0.5071, 0.4866, 0.4409], 
                [0.2673, 0.2564, 0.2762])
            ])

        self.full_data_dict, self.few_data_dict = self.load_data(root, train, dataset)

        print('full_data_num: %d' % count_data(self.full_data_dict))
        print('few_data_num: %d' % count_data(self.few_data_dict))

    def load_data(self, root, train, dataset):
        if dataset == 'cifar100':
            few_selected_label = random.Random(self.seed).sample(range(self.num_labels), self.nway)
            print('selected labeled', few_selected_label)

            full_data_dict = {}
            few_data_dict = {}

            d = CIFAR100(root, train=train, download=True)

            for i, (data, label) in enumerate(d):

                data = self.transform(data)

                if label in few_selected_label:
                    data_dict = few_data_dict
                else:
                    data_dict = full_data_dict

                if label not in data_dict:
                    data_dict[label] = [data]
                else:
                    data_dict[label].append(data)
            print(i + 1)
        else:
            raise NotImplementedError

        return full_data_dict, few_data_dict

    def load_batch_data(self, train=True, batch_size=16, nway=5, num_shots=1):
        if train:
            data_dict = self.full_data_dict
        else:
            data_dict = self.few_data_dict

        x = []
        label_y = [] # fake label: from 0 to (nway - 1)
        one_hot_y = [] # one hot for fake label
        class_y = [] # real label

        xi = []
        label_yi = []
        one_hot_yi = []
        

        map_label2class = []

        ### the format of x, label_y, one_hot_y, class_y is 
        ### [tensor, tensor, ..., tensor] len(label_y) = batch size
        ### the first dimension of tensor = num_shots

        for i in range(batch_size):

            # sample the class to train
            sampled_classes = random.sample(data_dict.keys(), nway)

            positive_class = random.randint(0, nway - 1)

            label2class = torch.LongTensor(nway)

            single_xi = []
            single_one_hot_yi = []
            single_label_yi = []
            single_class_yi = []


            for j, _class in enumerate(sampled_classes):
                if j == positive_class:
                    ### without loss of generality, we assume the 0th 
                    ### sampled  class is the target class
                    sampled_data = random.sample(data_dict[_class], num_shots+1)

                    x.append(sampled_data[0])
                    label_y.append(torch.LongTensor([j]))

                    one_hot = torch.zeros(nway)
                    one_hot[j] = 1.0
                    one_hot_y.append(one_hot)

                    class_y.append(torch.LongTensor([_class]))

                    shots_data = sampled_data[1:]
                else:
                    shots_data = random.sample(data_dict[_class], num_shots)

                single_xi += shots_data
                single_label_yi.append(torch.LongTensor([j]).repeat(num_shots))
                one_hot = torch.zeros(nway)
                one_hot[j] = 1.0
                single_one_hot_yi.append(one_hot.repeat(num_shots, 1))

                label2class[j] = _class

            shuffle_index = torch.randperm(num_shots*nway)
            xi.append(torch.stack(single_xi, dim=0)[shuffle_index])
            label_yi.append(torch.cat(single_label_yi, dim=0)[shuffle_index])
            one_hot_yi.append(torch.cat(single_one_hot_yi, dim=0)[shuffle_index])

            map_label2class.append(label2class)

        return [torch.stack(x, 0), torch.cat(label_y, 0), torch.stack(one_hot_y, 0), \
            torch.cat(class_y, 0), torch.stack(xi, 0), torch.stack(label_yi, 0), \
            torch.stack(one_hot_yi, 0), torch.stack(map_label2class, 0)]


    def load_tr_batch(self, batch_size=16, nway=5, num_shots=1):
        return self.load_batch_data(True, batch_size, nway, num_shots)

    def load_te_batch(self, batch_size=16, nway=5, num_shots=1):
        return self.load_batch_data(False, batch_size, nway, num_shots)

    def get_data_list(self, data_dict):
        data_list = []
        label_list = []
        for i in data_dict.keys():
            for data in data_dict[i]:
                data_list.append(data)
                label_list.append(i)

        now_time = time.time()

        random.Random(now_time).shuffle(data_list)
        random.Random(now_time).shuffle(label_list)

        return data_list, label_list

    def get_full_data_list(self):
        return self.get_data_list(self.full_data_dict)

    def get_few_data_list(self):
        return self.get_data_list(self.few_data_dict)

这段代码的类图如下：

self_DatasetLoader

Dataset

self_DatasetLoader 继承自 torch.utils.data 的 Dataset，其数据源来自：cifar100，cifar100是 pytorch 集成的数据源之一，可以直接下载下来，它包括 100 个分类，每个分类由 500 幅 $3\ast 32\ast 32$ 图片组成：

d = CIFAR100(root, train=train, download=True)

在初始化时，self_DatasetLoader 调用 load_data( )，得到两个字典（dict）：few_data_dict 和 full_data_dict，字典的 key 是image的分类标签 class（即有100个不同的 classes ），而 data 是对应的 image 数据（即：$3\ast 32\ast 32$），具体过程如下：load_data() 将 cifar100 中全部的 (image, class) load出来，之后，每幅 image 经 tv.transforms.Compose( ) 处理，分门别类组装进这两个字典中，这两个字典中数据是互斥的，如下图：

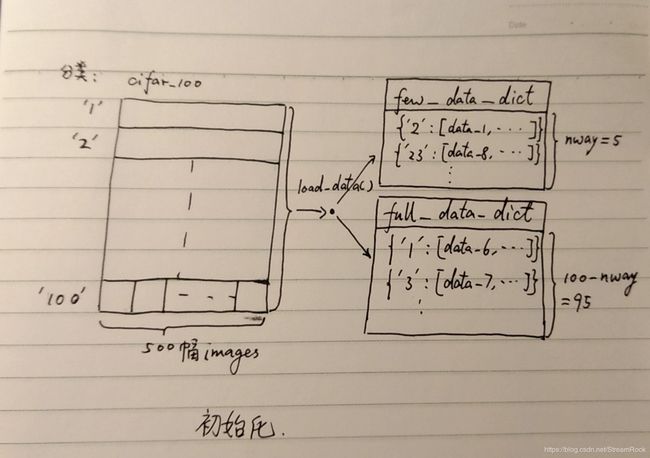
图3、数据源的初始化

在训练时，调用 load_tr_batch( ) -> load_batch_data( )方法，参数设置可取：train=True, batch_size=16, nway=5, num_shots=5。此时，训练数据来自于 full_data_dict ，如图4所示：

1. 从 full_data_dict 中随机抽取 nway=5 个类别，每个类别（class）指定一个序号，即：[0,1,2,3,4]，作为本次 task 数据的label，再在其中随机指定一个类别为 positive_class；
2. 从每个抽出的类别中，随机抽取 num_shots=5 幅 images，其中 positive_class 类别需要多抽一幅，即 6 幅；
3. 将 image、label、以及label对应的 one_hot，和它在原数据集的类别（class）等信息堆叠起来，形成批输出数据。
4. 批数据输出为

return [torch.stack(x, 0), torch.cat(label_y, 0), torch.stack(one_hot_y, 0), \
            torch.cat(class_y, 0), torch.stack(xi, 0), torch.stack(label_yi, 0), \
            torch.stack(one_hot_yi, 0), torch.stack(map_label2class, 0)]

其中，x 指 test set 数据，label_y 是它对应的 label（注意，并不是在原数据集中的分类，而是在本次 task 中的分类序号），one_hot_y 是 label_y 对应的 one_hot 编码，class_y 是它对应于原数据集的分类；xi 值 support set 数据，其它带 i 的数据项，也都是指 support set 的对应部分，其解释与不带 i 的相同。在 few-shot learning 中，一个训练数据称为一个 task 数据，它由 support set 和 test set 两部分构成，其中 test set 的 one_hot_y 将作为prediction的 ground-truth，从而形成有监督训练（supervise training）。如图4：

图4、获取一个 Task 数据

另外，前面设置了batch_size=16，即一次（batch）训练将构建 16 个task 数据，每个task 的构造皆如上述方法。
以下是训练时的数据加载（Trainer.train_batch( )) 的代码片段：

data = self.tr_dataloader.load_tr_batch(batch_size=args.batch_size, 
            nway=args.nway, num_shots=args.shots)

data_cuda = [tensor2cuda(_data) for _data in data]

self.opt.zero_grad()

logsoft_prob = self.model(data_cuda)

2.2 GNN 网络

【2】采用的深度网络如下图所示：

图5、《Few-Shot Learning with Graph Neural Networks》采用的网络

由图5，可见整个处理包括两部分：第一部分是一般的 CNN 网络，它的主要功能是处理 task 数据，其目的是将 task 中各图片和one-hot数据处理为后一部分 GNN 输入的张量 $\mathcal{T}$，这部分由 $\varphi (x)$ 完成；第二部分网络是 GNN，它是图神经网络，其目标是构建出一个条件分布 $p(Y|\mathcal{T})$，由此，可以对给定的一个 $\mathcal{T}$ predict 出分类 Y，此时 Y 对应的就是输入 task 数据的 label_y，并与它一起形成有监督学习的 Loss。
以下，本文将对各部分的实现进行详细展开。

2.2.1 特征提取网络

在代码实现中，$\varphi (x)$ 是由 EmbeddingCNN 实现的，它是一个标准的 CNN 网络：

###############################################################
## Vanilla CNN model, used to extract visual features

class EmbeddingCNN(myModel):

    def __init__(self, image_size, cnn_feature_size, cnn_hidden_dim, cnn_num_layers):
        super(EmbeddingCNN, self).__init__()

        module_list = []
        dim = cnn_hidden_dim
        for i in range(cnn_num_layers):
            if i == 0:
                module_list.append(nn.Conv2d(3, dim, 3, 1, 1, bias=False))
                module_list.append(nn.BatchNorm2d(dim))
            else:
                module_list.append(nn.Conv2d(dim, dim*2, 3, 1, 1, bias=False))
                module_list.append(nn.BatchNorm2d(dim*2))
                dim *= 2
            module_list.append(nn.MaxPool2d(2))
            module_list.append(nn.LeakyReLU(0.1, True))
            image_size //= 2
        module_list.append(nn.Conv2d(dim, cnn_feature_size, image_size, 1, bias=False))
        module_list.append(nn.BatchNorm2d(cnn_feature_size))
        module_list.append(nn.LeakyReLU(0.1, True))

        self.module_list = nn.ModuleList(module_list)

    def forward(self, inputs):
        for l in self.module_list:
            inputs = l(inputs)

        outputs = inputs.view(inputs.size(0), -1)
        return outputs

    def freeze_weight(self):
        for p in self.parameters():
            p.requires_grad = False```

调用它的部分在 gnnModel 的初始化部分：

class gnnModel(myModel):
    def __init__(self, nway):
        super(myModel, self).__init__()
        image_size = 32
        cnn_feature_size = 64
        cnn_hidden_dim = 32
        cnn_num_layers = 3

        gnn_feature_size = 32

        self.cnn_feature = EmbeddingCNN(image_size, cnn_feature_size, cnn_hidden_dim, cnn_num_layers)
        self.gnn = GNN(cnn_feature_size, gnn_feature_size, nway)

由以上代码可见 EmbeddingCNN 的初值设置，它最终将每一幅 image 处理成为一个 64 维特征矢量，其过程如下图所示：

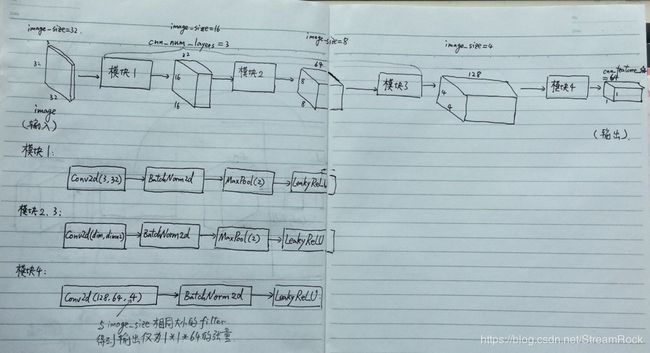
图6、EmbeddingCNN 处理流程

2.2.2 顶点表达

一个 task 中所有 images 通过 EmbeddingCNN 就可以得到一个 Graph 中所有 nodes 所需的特征矢量，一共是（nwaynum_shot+1 = 55+1=26）个特征矢量，它们还需要与对应的one-hot编码合起来，才能成为一个GNN 的输入$\mathcal{T}$。具体的处理代码在 gnnModel.forward( ) 中可以找到，如下：

def forward(self, data):
        [x, _, _, _, xi, _, one_hot_yi, _] = data

        z = self.cnn_feature(x)
        zi_s = [self.cnn_feature(xi[:, i, :, :, :]) for i in range(xi.size(1))]

        zi_s = torch.stack(zi_s, dim=1)


        # follow the paper, concatenate the information of labels to input features
        uniform_pad = torch.FloatTensor(one_hot_yi.size(0), 1, one_hot_yi.size(2)).fill_(
            1.0/one_hot_yi.size(2))
        uniform_pad = tensor2cuda(uniform_pad)

        labels = torch.cat([uniform_pad, one_hot_yi], dim=1)
        features = torch.cat([z.unsqueeze(1), zi_s], dim=1)

        nodes_features = torch.cat([features, labels], dim=2)

        out_logits = self.gnn(inputs=nodes_features)
        logsoft_prob = F.log_softmax(out_logits, dim=1)

        return logsoft_prob

从代码中，我们可以看到 GNN 的输入是 node_features，node_features 对应一个图 Graph 的顶点集，该顶点集的每一个顶点用一个特征值矢量表示，该特征值矢量由一幅 image 的 feature 和它的 one-hot 合成，就是图7中的一行，其中橙色部分表示feature，粉红部分表示 one-hot，如下：

图7、GNN输入$\mathcal{T}$ 的组成

图7中，每一行代表一幅image的数据，即：$\varphi (x)$ 部分（feature）与$h(l)$ 部分（one-hot），其中 Support set 部分的$h(l)$ 用image 对应的 one-hot 表示，而 test set 部分的 $h(l)$ 全部指定为 $1/nway$ ，如下：

uniform_pad = torch.FloatTensor(one_hot_yi.size(0), 1, one_hot_yi.size(2)).fill_(1.0/one_hot_yi.size(2))

uniform_pad = tensor2cuda(uniform_pad)

labels = torch.cat([uniform_pad, one_hot_yi], dim=1)

在代码实现中，默认 $\mathcal{T}$ 数据的第一条是要 predict 的数据。

综上，GNN 输入的是一个图 Graph 顶点集中各顶点的描述数据。对于以上程序，每一批次（batch）有16个图 Graph，每个图 Graph 有26个顶点，其中第一个顶点的类别是需要 predict 的，其余25个顶点的描述数据是齐备的，包括了feature和它对应的one-hot。GNN 的目标就是要依据$\mathcal{T}$ ，建立顶点间的连接关系。

2.2.3 卷积图神经网络——Convolutional Graph Neural Networks (ConvGNNs)

《Few-Shot Learning with Graph Neural Networks》【2】目标是要完成 test set 中 node 的分类推断，它需要借助于图神经网络 GNN。
GNN 的目标是习得一个网络，当我们给它输入一组顶点的表达（Representation），它就能输出相关的图 Graph 的结构，也就是各顶点之间的关系，即边（Edge）的连接关系。Graph 一般可以用 $G(V,E)$ 表示，其中 $V$ 表示顶点（Vertix）的集合，$E$ 表示边（Edge）集合，我们可以用 Adjacency Matrix（邻接矩阵）表示顶点与顶点间的连接关系。
《Few-Shot Learning with Graph Neural Networks》【2】所采用的 GNN 是卷积图神经网络（ConvGNNs）。ConvGNN 可分为两种【3】：一种是基于谱的 Spectral-based ConvGNNs，另一种是基于空间的 Spatial-based ConvGNNs。前者有坚实的理论基础，但后者更简单、灵活高效，且通用性高，近年来发展非常快，【2】选用的GNN 就是这种。
Spatial-based ConvGNNs 的思想来源于另一种被称为递归 GNN 的Recurrent Graph Neural Networks (RecGNNs)【3】。它的基本思想是：

Based on an information diffusion mechanism, GNN updates nodes’ states by exchanging neighborhood information recurrently until a stable equilibrium is reached.【3】

简单地说，就是信息在网络中传播，经过若干轮递归就能稳定，这就是最终的信息表达。此处的信息包括：节点信息，边的信息等，可以是一切与 Graph 相关的 information。RecGNNs 每次迭代都用相同的递归层来处理 ，而 Spatial-based ConvGNNs 则用不同卷积层来代替不同阶段的递归层，如下图【3】所示。

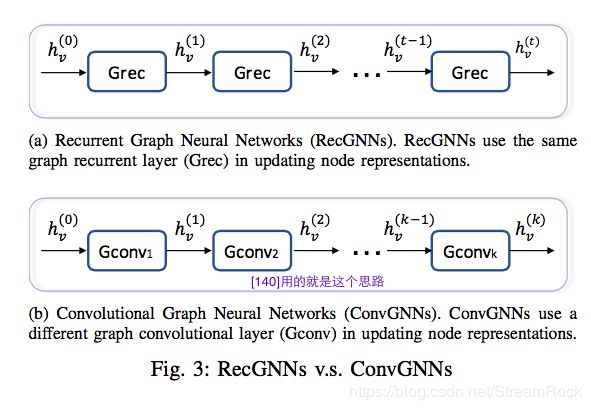
图8、RecGNNs V.S. ConvGNNs

图9、GNN 处理流程

图9是【2】的GNN处理流程，图中自左到右的第三个方框中的 ${\bar{A}}_{i,j}^{(k)}$，应该改为：${\bar{A}}_{i,j}^{(k+1)}$。该图可以这样理解：
1、各色圆圈代表 Graph 中的各顶点，不同颜色表示顶点的 Representation 不同，从图中可以看到不同顶点颜色不同，不同层次，即使是相同的顶点 Representation 也不同。
初始的顶点集表达如下：
$${\mathbf{x}}^{(0)}=\{(\varphi (x_i),h(l_i)){\}}_{i\in \mathcal{T}}$$
其中, $\varphi (x_i)$ 表示第 i 幅 image 经过 EmbeddingCNN 得到的特征矢量，$h(l_i)$ 表示其分类所对应的 one-hot 编码，${\mathbf{x}}^{(0)}$ 表示第0层（初始）的 Information。

2、构建邻接矩阵（Adjacency Matrix），对应第 k 层 Information 的是${\bar{A}}^{(k)}$，它的每一个元是：
$${\bar{A}}_{i,j}^{(k)}={\phi }_{\bar{\theta }}({\mathbf{x}}_i^{(k)},{\mathbf{x}}_j^{(k)})(1)$$
其中
$${\phi }_{\bar{\theta }}({\mathbf{x}}_i^{(k)},{\mathbf{x}}_j^{(k)})=ML{P}_{\bar{\theta }}(abs({\mathbf{x}}_i^{(k)},{\mathbf{x}}_j^{(k)}))(2)$$
式（2）中 ${\phi }_{\bar{\theta }}({\mathbf{x}}_i^{(k)},{\mathbf{x}}_j^{(k)})$ 表示 i、j 两个顶点（nodes）之间相似度的测度，该测度并不固定，而是通过经训练的多层神经网络 MLP 而得到， MLP的输入是两个节点（nodes）特征矢量差的绝对值。
3、获得 ${\bar{A}}^{(k)}$ 后，邻接矩阵 ${\bar{A}}^{(k)}$ 与对应层特征矢量 ${\mathbf{x}}^{(k)}$ 相乘，然后进行一个加权处理，即乘一个权重 ${\theta }_l^{(k)}$（在实现时，通过一个 nn.Linear 实现），加权结果再经过一个逐点非线性处理 $\rho (\cdot )$ 最终得到下一层特征表达 ${\mathbf{x}}^{(k+1)}$，其数学表达式如下：
$${\mathbf{x}}_l^{(k+1)}=Gc({\mathbf{x}}_l^{(k)})=\rho \left(\sum {\bar{A}}^{(k)}{\mathbf{x}}^{(k)}{\theta }_l^{(k)}\right),l=d_1,\cdots ,d_{k+1}(3)$$
式中 $l$ 表示特征矢量的第 l 维，从上面实现可见，第 k 层特征表达与第 k+1 层的特征表达的维度是可以不同的，这由 nn.Linear 的输入与输出维度决定。
具体代码如下：

class Graph_conv_block(nn.Module):
    def __init__(self, input_dim, output_dim, use_bn=True):
        super(Graph_conv_block, self).__init__()

        self.weight = nn.Linear(input_dim, output_dim)
        if use_bn:
            self.bn = nn.BatchNorm1d(output_dim)
        else:
            self.bn = None

    def forward(self, x, A):
        x_next = torch.matmul(A, x) # (b, N, input_dim)
        x_next = self.weight(x_next) # (b, N, output_dim)

        if self.bn is not None:
            x_next = torch.transpose(x_next, 1, 2) # (b, output_dim, N)
            x_next = x_next.contiguous()
            x_next = self.bn(x_next)
            x_next = torch.transpose(x_next, 1, 2) # (b, N, output)

        return x_next

class Adjacency_layer(nn.Module):
    def __init__(self, input_dim, hidden_dim, ratio=[2,2,1,1]):

        super(Adjacency_layer, self).__init__()

        module_list = []

        for i in range(len(ratio)):
            if i == 0:
                module_list.append(nn.Conv2d(input_dim, hidden_dim*ratio[i], 1, 1))
            else:
                module_list.append(nn.Conv2d(hidden_dim*ratio[i-1], hidden_dim*ratio[i], 1, 1))

            module_list.append(nn.BatchNorm2d(hidden_dim*ratio[i]))
            module_list.append(nn.LeakyReLU())

        module_list.append(nn.Conv2d(hidden_dim*ratio[-1], 1, 1, 1))

        self.module_list = nn.ModuleList(module_list)

    def forward(self, x):
        X_i = x.unsqueeze(2) # (b, N , 1, input_dim)
        X_j = torch.transpose(X_i, 1, 2) # (b, 1, N, input_dim)

        phi = torch.abs(X_i - X_j) # (b, N, N, input_dim)

        phi = torch.transpose(phi, 1, 3) # (b, input_dim, N, N)

        A = phi

        for l in self.module_list:
            A = l(A)
        # (b, 1, N, N)

        A = torch.transpose(A, 1, 3) # (b, N, N, 1)

        A = F.softmax(A, 2) # normalize

        return A.squeeze(3) # (b, N, N)

class GNN_module(nn.Module):
    def __init__(self, nway, input_dim, hidden_dim, num_layers, feature_type='dense'):
        super(GNN_module, self).__init__()

        self.feature_type = feature_type

        adjacency_list = []
        graph_conv_list = []

        # ratio = [2, 2, 1, 1]
        ratio = [2, 1]

        if self.feature_type == 'dense':
            for i in range(num_layers):
                adjacency_list.append(Adjacency_layer(
                    input_dim=input_dim+hidden_dim//2*i, 
                    hidden_dim=hidden_dim, 
                    ratio=ratio))

                graph_conv_list.append(Graph_conv_block(
                    input_dim=input_dim+hidden_dim//2*i, 
                    output_dim=hidden_dim//2))

            # last layer
            last_adjacency = Adjacency_layer(
                        input_dim=input_dim+hidden_dim//2*num_layers, 
                        hidden_dim=hidden_dim, 
                        ratio=ratio)

            last_conv = Graph_conv_block(
                    input_dim=input_dim+hidden_dim//2*num_layers, 
                    output_dim=nway, 
                    use_bn=False)

        elif self.feature_type == 'forward':
            for i in range(num_layers):
                adjacency_list.append(Adjacency_layer(
                    input_dim=input_dim if i == 0 else hidden_dim, 
                    hidden_dim=hidden_dim, 
                    ratio=ratio))

                graph_conv_list.append(Graph_conv_block(
                    input_dim=hidden_dim, 
                    output_dim=hidden_dim))

            # last layer
            last_adjacency = Adjacency_layer(
                        input_dim=hidden_dim, 
                        hidden_dim=hidden_dim, 
                        ratio=ratio)

            last_conv = Graph_conv_block(
                    input_dim=hidden_dim, 
                    output_dim=nway,
                    use_bn=False)

        else:
            raise NotImplementedError

        self.adjacency_list = nn.ModuleList(adjacency_list)
        self.graph_conv_list = nn.ModuleList(graph_conv_list)
        self.last_adjacency = last_adjacency
        self.last_conv = last_conv


    def forward(self, x):
        for i, _ in enumerate(self.adjacency_list):
            adjacency_layer = self.adjacency_list[i]
            conv_block = self.graph_conv_list[i]

            A = adjacency_layer(x)

            x_next = conv_block(x, A)

            x_next = F.leaky_relu(x_next, 0.1)

            if self.feature_type == 'dense':
                x = torch.cat([x, x_next], dim=2)
            elif self.feature_type == 'forward':
                x = x_next
            else:
                raise NotImplementedError
        
        A = self.last_adjacency(x)
        out = self.last_conv(x, A)   

        return out[:, 0, :]

这里，一层处理包含两个模块：

• Adjacency_layer 由Conv（卷积）搭建出来，负责获得邻接矩阵 ${\bar{A}}^{(k)}$
• Graph_conv_block 负责完成上述步骤3。

这两个模块构成一个 $Gc(\cdot )$，通过堆叠 $Gc(\cdot )$ 可构建多层卷积图神经网络，如图8（b）。

2.2.4 Loss的解析

GNN_module 最后通过一个 Graph_conv_block 输出：

last_conv = Graph_conv_block(
                    input_dim=hidden_dim, 
                    output_dim=nway,
                    use_bn=False)

输出的是一个矢量，其维度是 nway。此矢量再通过 softmax 形成 nway 分类的概率，对应待预测的 test set （此处 test set 只有一个样本）的 lable 的分布概率，具体如下（代码在 trainer.py -> gnnModel -> forward() ）：

out_logits = self.gnn(inputs=nodes_features)
logsoft_prob = F.log_softmax(out_logits, dim=1)

我们回顾一下前面内容，一开始，我们先随机获得 nway=5 个分类，然后为这 nway 个分类分配类别号（label），如：0、1、2、3、4，而不再使用原来的类别（class）；在这 nway 个分类中，再随机选取一个作为 positive 分类；接着，在这些分类中随机抽取 num_shots=5 张 images，并设置好对应 one-hot，构成 Support set，而 positive 分类则多抽取 1 张，此 image 的 one-hot 设定为未知，需要perdict，在经过了 GNN 之后，输出的这个 logsoft_prob 就是它的分类预测概率。由于这是多分类问题，因此选择了：

loss = F.nll_loss(logsoft_prob, label)

上述代码中 label 就是 positive 类别对应的 one-hot 编码，而 nll_loss 就是：The negative log likelihood loss. It is useful to train a classification problem with C classes. 简单来说就是适用于多分类的 negative log likelihood loss。
如此，GNN 便形成了有监督训练。原文的表述是这样的：

In this setup, the model is asked only to predict the label $Y$ corresponding to the image to classify $\bar{x}\in \mathcal{T}$, associated with node $\ast$ in the graph. The final layer of the GNN is thus a softmax mapping the node features to the K-simplex. We then consider the Cross-entropy loss evaluated at node $\ast$ :
$l(\Phi (\mathcal{T};\Theta ),Y)=-{\sum }_k{y}_k\log P(Y_{\ast }=y_k|\mathcal{T})$

到此，用于 Few-shot learning 的网络构建完毕，可以进行学习训练了。

三、总结

Graph 图反映了数据点之间的结构关系，可以用矩阵的方式来表达它，比如：Adjacency Matrix （邻接矩阵），而 GNN 图神经网络可为我们习得 Graph 图的关系，也即获得 Adjacency Matrix （如本文），从而使我们能够依据图的关系进行推断。本文的 Few-shot 推断是依据数据点之间的图关系进行类别的 prediction 的方法，可以解决类别数量不预先确定的推断问题，也可以解决依据小样本进行推断的实际问题。
另外，本文所述方法是将两个不同的网络（CNN、GNN）进行联合训练的例子，其一是一般的图像卷积神经网络，以提取图像的特征表达；另一个为卷积图神经网络，它通过在 nodes 的特征差上构建 Adjacency Matrix 矩阵，完成图的学习。两者的意义和目的相差巨大，虽然整个过程是 end-to-end 的，但这样硬生生地将两个不同网络结合的方法就是最优的吗？是否会出现不和谐的声音，比如：梯度消失、梯度爆炸，又或者是最优解不稳定，泛化能力弱等问题？给我感觉就是：当前的网络设计就像是“头痛医头，脚痛医脚”，凡是自己没把握的就交给网络来做，殊不知网络的拟合能力虽强，但同时也带来了过耦合、无穷局部最优等的问题，这种生硬的 end-to-end 方法可能就是带来这个问题的重要原因。
最后，图神经网络 GNN 是神经网络走向复杂推断的重要路径，是近年来深度学习的热点。在 GNN 的学习过程中，我发现了一个很好的资源【5】，今后有空可以好好研究一下。

索引

---

【1】小样本学习（Few-shot Learning）综述 https://www.chainnews.com/articles/650132977783.htm
【2】Garcia V , Bruna J . Few-Shot Learning with Graph Neural Networks[J]. 2017. https://arxiv.org/abs/1711.04043v3
【3】Wu Z , Pan S , Chen F , et al. A Comprehensive Survey on Graph Neural Networks[J]. 2019. https://arxiv.org/abs/1901.00596?context=cs
【4】https://github.com/louis2889184/gnn_few_shot_cifar100
【5】关于图神经网络（GNN）的必读文章 https://python.ctolib.com/thunlp-GNNPapers.html