有限元法基本思想和分类

1 有限元法基本思想

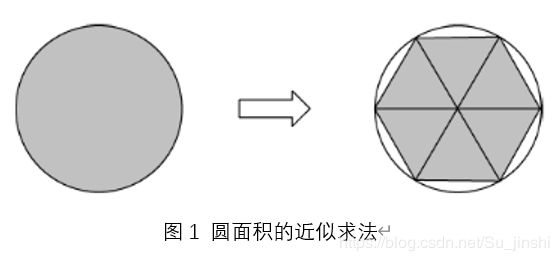
有限元法是在连续体上直接进行近似计算的一种数值方法，其基本思想通过下面的例子来说明。图1简答说明了早期数学上求解圆面积的近似方法。首先将连续的圆分割成一些三角形，求出每个三角形的面积，再将每个小三角形面积相加，即可得到圆面积的近似值。前面是“分”的过程，后面是“合”的过程。之所以要分，是因为三角形面积容易求得。这样简单的一分一合，就很容易求出圆面积的近似值。体现了有限元法的基本思想，即“拆整为零，集零为整”。

“拆整为零”即“分”的过程，具体包括

1）离散化

将连续的求解区域离散为有限个部分的集合，并认为各部分只通过有线个点连接起来。例如图2，可假想连续体（a）由许多小部件（b）组成，这些规则或不规则的小部分成为单元（element）。单元之间只通过有限个点连接起来，如（c）所示，单元①与单元②只在1、2两点相连，这些连接点称为节点（node）。这一过程称有限元离散化过程。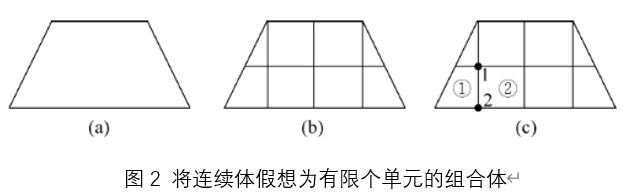

2）假定单元场函数

在每个单元内假定近似场函数（位移函数或应力函数），并将单元内的场函数由该单元各个节点的数值通过函数插值表示，这样，未知的场函数（或包括其导数）在单元内各个节点的数值就成为新的未知量（其个数称为自由度），从而使一个连续的无限自由度问题变成离散的有限自由度问题。

3）单元分析

对每个单元分析，求出单元的特性。

“集零为整”即“合”的过程，将单元的特性装配在一起得到离散体整体的特性，并利用数值计算方法得到整个求解域上场函数的近似值。

2 有限元法分类

   有限元法按基本未知量可分为三大类，即有限元位移法、有限元力法、有限元混合法。在有限元位移法中，选节点位移作为基本未知量；在有限元力法中，选节点力作为基本未知量；在有限元混合法中，一部分基本未知量为节点位移，另一部分基本未知量为节点力。有限元位移法计算过程的系统性、规律性强，特别适宜编程求解。一般除板壳问题的有限元法应用一定量的混合法外，其余全部采用有限元位移法。

  有限元法按求解问题的类型可分为两大类：线弹性有限元法和非线性有限元法。其中线弹性有限元法是非线性有限元法的基础。

1）线弹性有限元法

线弹性有限元法以理想弹性体为研究对象，所考虑的变形建立在小变形假设的基础上。具体讲，下面四条必须同时满足的问题为线弹性问题：

1. 材料的应力与应变呈线性关系，满足广义胡克定理。
2. 应变与位移的一阶导数呈线性关系。
3. 微元体的平衡方程是线性的。
4. 结构的边界条件是线性的。

线弹性有限元问题归结为求解线性方程组问题，所需时间较少。

线弹性有限元一般包括弹性静力学分析与线性弹性动力学分析两个主要内容。学习这些内容需具备材料力学、结构力学、弹性力学、振动力学、数值方法、矩阵代数、算法语言等方面的知识。

2）非线性有限元法

有限元法所求解的非线性问题可以分为如下三类

1. 材料非线性问题。在线弹性问题的四个条件中，不满足第1条的称为材料非线性问题。

       材料的非线性问题中，材料的应力和应变呈非线性关系。在工程实际中较

为重要的材料非线性问题有：非线性弹性（包括分段线弹性）、弹塑性、黏塑性及蠕变等。

     2. 几何非线性问题。在线弹性问题的四个条件中，不满足2、3条的称

为几何非线性问题。

      几何非线性由结构变形的大位移造成。一般分两类：一类叫小变形几何非线性问题，在这类问题中应变很小，但不能忽略高阶应变，所以它可以表述为结构在加载过程中不能忽略小应变的有限转动的弹性力学问题，如薄板的大挠度问题就属于小变形几何非线性问题；另一类叫有限变形（或大应变）几何非线性问题，在这类问题中，结构将产生很大的变形和位移，变形过程已经不可能直接用未受力时的位置和形态加以描述，平衡状态的几何位置也是未知的，而且必须给出应力、应变的新定义。由此可见，有限变形（或大应变）几何非线性问题的求解有别于小变形几何非线性问题，如橡胶部件形成过程与金属塑性加工过程均为有限变形几何非线性问题。

     3. 边界非线性问题。在线弹性问题的四个条件中，不满足第4条的称为

边界非线性问题。

          边界非线性包括两个结构物的接触边界随加载和变形而改变引起的接触非       线性，也包括非线性弹性地基的非线性边界条件和可动边界问题等。

           在加工、密封、撞击等问题中，接触和摩擦的作用不可忽视，接触边界属 于高度非线性边界。齿轮啮合、冲压成型、轧制成像、橡胶减震器、紧配合装配等都是一些接触问题。当一个结构与另一个结构或外部边界相接触是通常要考虑非线性边界条件

     实际的非线性可能出现上述两种或三种非线性问题。

     上述三类非线性问题与线弹性问题的求解有很大不同，主要表现在如下三个方

面：

1. 非线性问题的方程是非线性的，一般需求迭代求解。
2. 非线性问题的解不一定是唯一的，有时甚至没有解。
3. 非线性问题解的收敛性事先不一定能得到保证，可能出现振荡或发散现象。

以上三方面的因素使非线性问题的求解过程比线弹性问题更加复杂、费用更高和更具有不可预知性。