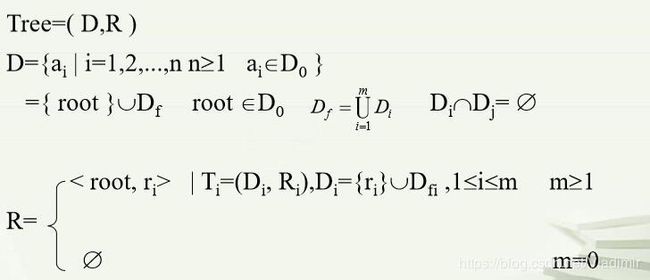数据结构：树与二叉树（一） 树的基本知识

这篇文章给大家简单讲一下树。

1.树逻辑结构

（1）树（Tree）是一个非空的有限元素的集合，元素之间有如下关系：有且仅有一个特殊元素，它没有前驱（称为树根Root），其余元素都有且仅有一个前驱元素，所有的元素（报货树根元素）可以有零个或多个后继。

（2）树的递归定义：树T是一个非空数据元素的有限集合，其中有且仅有一个 特定元素称为树T的根，剩余的元素（若有的话）可被划分为 m 个互不相交的集合 T1，T2，... ，Tm，而每个集合又都是树， 称为T的子树( Subtree ) 。

特点：除根外，每个元素有且仅有一个前驱元素，有零个或多个后继元素。

（3）树数据结构的形式化定义：

说实话，这些知识太久远了，有些地方我也不知道自己理解的对不对。上面这张图中，D是数据集合，R是数据之间的关系，按照我的理解，上面的这个形式化定义，应该是通过定义根与其子树根之间的关系来定义树的。各个子树的根分别为r1,r2,r3...,rm，它们以root（它们自己的上层元素，不是树根的那个root）为前驱元素。D是根的集合，包括树根root（这个root是树根的那个root）；R是根与各子树根之间的关系，其实就是相连关系。

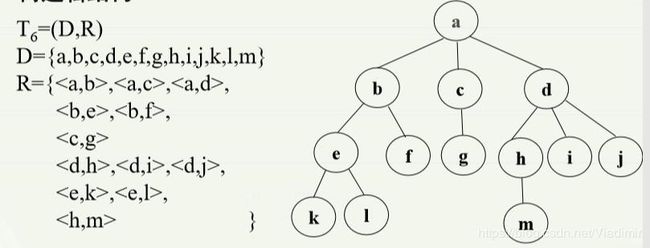
举个例子：

（4）树数据结构的术语：

结点	树中的每一个数据元素都被称为一个结点（比如上面那棵树，a、b、c到m被称为结点）
结点的度（degree）	任一结点子树的树目（其实就是这个结点的后继结点的数目，比如上面这棵树，结点a的度为3，结点b的度为2，结点c的度为1）
叶子（leaf）	度为零的结点，又称为末端结点（如上面那棵树的结点k、l、f、m等）
分支结点	度不为零的结点，又称为非末端结点（如上面那棵树的结点b、e、c等）
分支	结点之间的关系（如上面那棵树的{d，e}、{d，f}等）
内部结点	除根之外的分支结点（如上面那棵树的结点b、e、h、i等）
树的度	树中结点度的最大值（K叉树，如上面那棵树，树的度就是结点d和a的度，为3，所以上面这棵树是三叉树）
孩子（儿子）	结点的子树的根成为该结点的孩子（意思就是这个结点所有的后继结点都是该结点的儿子，如上面这棵树中，结点b的儿子有e、f）
双亲（父亲）	一个结点是它各子树的根结点的双亲（前趋，比如上面那棵树，结点e的双亲就是结点b）
兄弟（sibling）	具有相同双亲的结点（比如上面那棵树，e和f就是兄弟）
祖先	从根结点到该结点路径上所有结点都称为该结点的祖先（比如上面那棵树，结点e的祖先有b和a）
子孙	该结点所有子树上的结点都称为该结点的子孙（比如上面那棵树的结点b，它的子孙 结点有e、f、k、l）
结点的层次	根结点定义为第1层，根的儿子定义为第2层，... ，依次类推。记作 L(v)
树的深度 （高度）	各个结点层次的最大值（比如上面那棵树，深度为4）
堂兄弟	双亲在同一层上的结点（比如上面那棵树，结点e和结点g就是堂兄弟）
有序树	结点的子树（后继）是有顺序的（兄弟有大小、 先后之分）
路径	树中的k个结点n1,n2,...,nk，满足 ni是 ni+1的 双亲，称n1到nk有一条路径
路径长度	路径长度=路径上结点个数-1

树根root没有双亲，叶子结点没有孩子；vi是vj的双亲，则L（vi）=L（vj）-1。

 

2.树逻辑结构表示方法（树的画法）

（1）直观表示法：

用圆圈表示结点，元素写在圆圈中，连线表示元素之间的关系根在上， 叶子在下（即树向下生长）。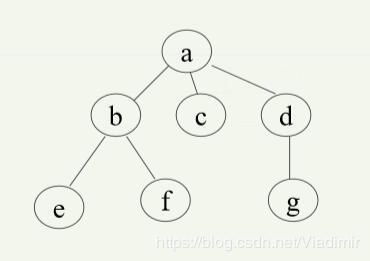

（2）集合表示法：

根据树的集合定义，写出集合划分。

{ a, {b,{e},{f}}, {c}, {d,{g}} }
上面这个集合，就是（1）中那棵树的集合表示。

（3）文氏图表示法：

集合表示的一种直观表示，用图表示集合。

这个图，也是（1）中那棵树的表示。

（4）目录表示法（凹入表示法）：

好吧，这个图，也是（1）中那棵树的表示。

（5）广义表表示法：

将一棵树描述为一个广义表，树根为单元素，子树就对应字表。

( a, (b,(e),(f) ), (c), (d,(g) ) )

 

3.树逻辑结构的性质

性质1：树中的结点个数等于所有结点的度加1。

性质2：度为k的树（k叉树）中第i层上最多有k^(i-1)个结点。（i≥1）

性质3：深度为h的k叉树最多有 (k^h-1)/(k-1)个结点。

性质4：有n个结点的k叉树的最小深度为[log(k)(n*(k-1)+1)]

 

4.树逻辑结构定义的操作

（1）初始化Create(t)：创建空树

（2）求树的根结点 Root(t)

（3）求某结点的双亲 Parent(t,x)

（4）求某结点的最左孩子 Left_Child(t,x)

（5）求某结点的右兄弟 Right_Sibling(t,x)

（6）遍历 Traver(t)：将树中结点访问而且仅访问一遍。

（7）求深度 Depth(t)

（8）插入

（9）删除

 

5.树ADT

树的抽象类定义：

 

6.树的存储结构

存储元素，表示关系。

树，可以顺序存储，也可以链式存储。对于树来说，存储元素简单，表示关系困难。

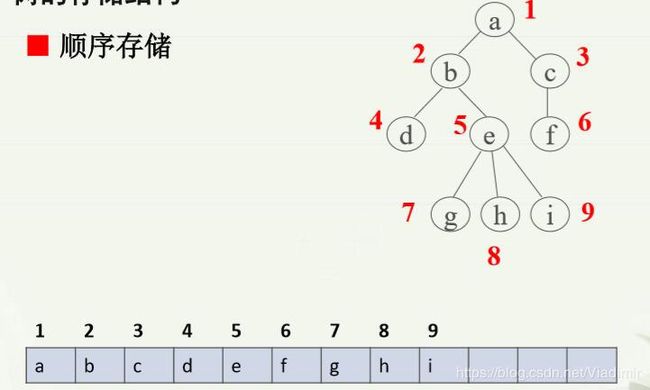
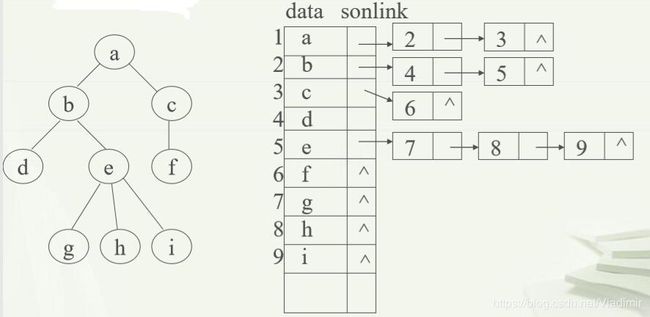
（1）顺序存储

分配连续空间 ，依次存放树的各个元素。

可约定：从上至下、从左至右将树的结点依次存入连续内存空间。

这种约定，存起来很简单，但是不能很好的表示关系。

举例：

（2）链式存储

用任意的存储空间，存放数据元素，在存储元素的同时存放其他相关元素的地址。

链式存储会产生一个问题：需要开辟几个指针？由此问题产生两种结点，定长节点与不定长节点。

不定长结点：

data：数据元素

c1,c2,...,cdi:指针，指向孩子结点

di：结点的度

存储n个结点的树，有n-1个指针。计算方法：因为每个结点有且仅有一个父亲结点，即一个指针，n个结点就有n个指针，因为树根结点没有父亲结点，所以总共有n-1个指针。

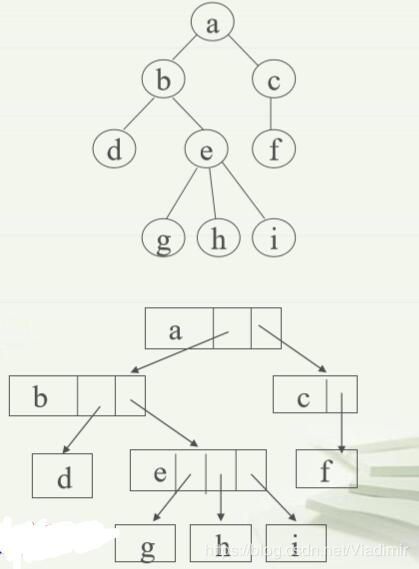
然后就是定长结点，定长结点会产生两个问题，一个是孩子结点太少，浪费存储空间；另一个是孩子结点太多，有可能超出结点可承受的孩子数量。

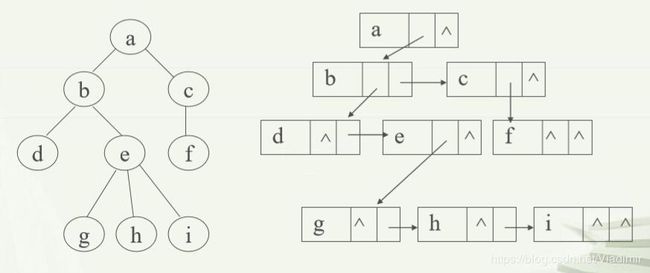
上面那棵树，定长结点的表示为：

这样的存储方式，若是孩子结点数量都不超出其父亲结点的承受能力，那么一共有n-1个指针，空指针有3*n-(n-1)=2*n+1个结点。

（3）其他存储方式

①

②

总的来说，树的存储结构有很多种，但是都有一个问题，就是存储简单的不好表示关系，好表示关系的存储起来不简单（当然，是对于普通的树，二叉树则不一样，这个我后面的博客会讲）。事情，都是有两面性的。