归并排序详解merge sort python代码实现

归并排序中采用的分而治之(divide-and-conquer)的思想. 把大问题(原问题)拆成一个一个相似的小问题，然后对这些小问题采用相同的方法进行处理，再最后合并各个小问题的答案，最后就得到了原问题的答案。
在讲怎么把原问题分解成一个一个小问题之前，我们需要一个合并函数来将两个无序的序列合并成一个有序的序列
1 现在我们手里有三个序列， 一个是未排序的序列A: [19, 21, 3, 1, 23, 6, 3, 10, 65, 78, 21,41]，它的左半部分的序列L为: [19, 21, 3, 1, 23, 6]和右半部分的序列R为: [3, 10, 65, 78, 21, 41]。
2. 假设左边的序列L: [19, 21, 3, 1, 23, 6] 排好序后的序列为[1, 3, 5, 19, 21, 23]，假设右边R序列[3, 10, 21, 41, 65, 78]已经排好序，这个有序的序列为[3, 10, 21, 41, 65, 78]（注意：我们将用排好序的L和R来进行合并得到最后的有序序列A ）
3. 现在写一个合并函数将序列L[1, 3, 5, 19, 21, 23]和序列R: [3, 10, 21, 41, 65, 78]合并为我们最后要得到的有序序列A[1, 3, 3, 6, 10, 19, 21, 21, 23, 41, 65, 78]
3.1合并函数的过程：
3.1.1 将L第一个元素与R第一个元素做比较，将两者之间最小的这个元素放在序列A索引为0的位置上
3.1.2 假设在步骤a中L的第一个元素最小，于是A中的第一个元素为L[0], 再将L中的第二个元素与R中第一个元素做
比较，将最小的元素放入A序列的第二个元素位置。
3.1.3 按步骤b那样，一直循环进行下去依次将L和R中较小的元素按顺序放入序列A中。如果在此过程中
序列L先循环完毕，就可以把R中的所有元素加入A序列中。因为R本来就是有序的，剩下的未循环
的必定也是有序的。这样下来就将有序的左半部分序列L和右半部分序列R合并成了我们最后想要
的有序序列A
3.2 合并的代码如下：

# this function is goting to merge two sorted sequences together
def merge(R,L):
    A=[]
    l=r= 0
    nr,nl=len(R),len(L)
    while nl>=1 and nr>=1: 
        if L[l]<=R[r]:
            A.append(L[l])
            nl-=1
            l+=1
        else:
            A.append(R[r])
            nr-=1
            r+=1
    if nl==0:
        A+=R[r:]
    if nr==0:
        A+=L[l:]
    return A

接下来讲解怎么把原问题分解下一个个小问题的思想：
将原来需要排序的序列拆分成左右两部分序列，接着又对左右的两部分序列进一步又拆分成左右两部分序列，过程如图：

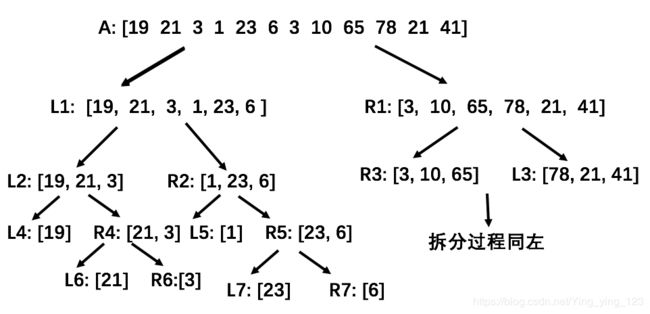
最后我们将会得到向L6，R6，L7和R7这样只包含一个元素的小列表。此时这个列表只有一个元素必定就是有序的了。接下来我们对这些子列表进行合并。合并L6和R6我们将得到有序的R4。合并L7和R7我们将得到有序的R5。合并有序的L4和R4我们将会得到有序的L2。依次进行合并下去最后我们会得到最后想要的目标序列：有序A。这个过程将使用递归来实现，递归的过程中结合合并函数，递归的出口为最后只分割成一个元素。当只有一个元素的时候就退出递归返回该序列。代码如下：

def merge_sort(A):
    na = len(A)
    if na == 1:
        return A
    mid = int(na/2)
    R=merge_sort(A[:mid])
    L=merge_sort(A[mid:])
    return merge(R,L)
if __name__ == '__main__':
    A = merge_sort([27,9,3,24,2,4,58,6,2,10,15,1,71,4])
    print (A)