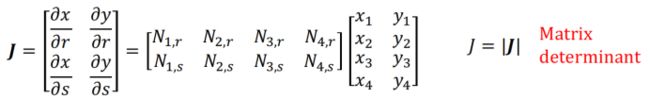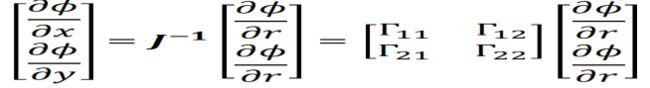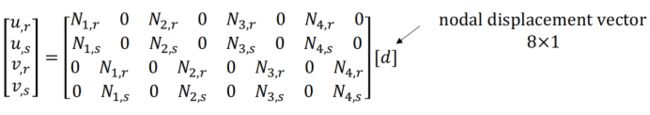简单有限元分析python实现——二维1单元4节点刚度矩阵求解然后得到4个节点的位移和力

2020数值分析作业，已成功实现功能，可直接复制代码就能实现

1、先给出大概的理论推导过程

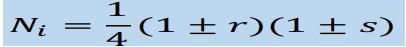
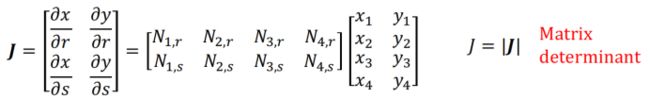
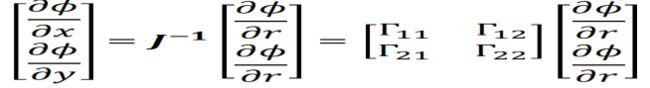
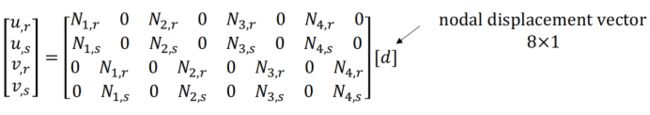
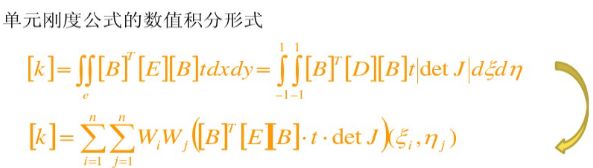
这里取高斯点坐标为Ɛ=-Ƞ=1/，权重为W1=W2=1

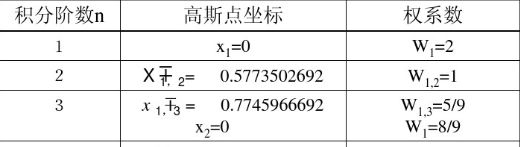
2、边界条件和解题思路如下

3、源代码双手奉上

from math import *
import numpy as np
# from  my_inv import invmat # 自己在网上看的矩阵求逆方法
# from LU import my_LUsolve # LU解线性方程


# 1个单元四个节点
def shapefunction(r,s):#形函数
    N1 = 1 / 4 * (1 - r) * (1 - s)
    N2 = 1 / 4 * (1 + r) * (1 - s)
    N3 = 1 / 4 * (1 + r) * (1 + s)
    N4 = 1 / 4 * (1 - r) * (1 + s)
    return N1,N2,N3,N4

def diffNdr(r,s): # 求dNidr
    dN1dr = 1 / 4 * (-1) * (1 - s)
    dN2dr = 1 / 4 * (1) * (1 - s)
    dN3dr = 1 / 4 * (1) * (1 + s)
    dN4dr = 1 / 4 * (-1) * (1 + s)
    dNdr = [dN1dr,dN2dr,dN3dr,dN4dr]
    return dNdr


def diffNds(r,s): # 求dNids
    dN1ds = 1 / 4 * (1 - r) * (-1)
    dN2ds = 1 / 4 * (1 + r) * (-1)
    dN3ds = 1 / 4 * (1 + r) * (1)
    dN4ds = 1 / 4 * (1 - r) * (1)
    dNds = [dN1ds, dN2ds, dN3ds, dN4ds]
    return dNds

def jacobian(x,y,r,s): # 求J,Jinv,Jdet
    dNdr = diffNdr(r,s)
    dNds = diffNds(r,s)

    dxdr = x[0]*dNdr[0]+x[1]*dNdr[1]+x[2]*dNdr[2]+x[3]*dNdr[3]
    dxds = x[0]*dNds[0]+x[1]*dNds[1]+x[2]*dNds[2]+x[3]*dNds[3]
    dydr = y[0]*dNdr[0]+y[1]*dNdr[1]+y[2]*dNdr[2]+y[3]*dNdr[3]
    dyds = y[0]*dNds[0]+y[1]*dNds[1]+y[2]*dNds[2]+y[3]*dNds[3]

    J = np.array([[dxdr,dxds],[dydr,dyds]])
    Jdet = np.linalg.det(J)
    # Jdet = J[0][0]*J[1][1]-J[0][1]*J[1][0]
    # Jinv = invmat(J) # 矩阵求逆函数
    Jinv = np.linalg.inv(J)
    return Jinv,Jdet

def Bmatrix(r,s,Jinv):# 求B
    dNdr = diffNdr(r, s)
    dNds = diffNds(r, s)

    B1 = np.matrix([[1,0,0,0],[0,0,0,1],[0,1,1,0]])
    B2 = np.zeros((4,4))
    B2[0:2,0:2] = Jinv
    B2[2:4,2:4] = Jinv
    B3 = np.zeros((4,8))
    B3[0,0] = dNdr[0]
    B3[0, 2] = dNdr[1]
    B3[0, 4] = dNdr[2]
    B3[0, 6] = dNdr[3]
    B3[1, 0] = dNds[0]
    B3[1, 2] = dNds[1]
    B3[1, 4] = dNds[2]
    B3[1, 6] = dNds[3]
    B3[2, 1] = dNdr[0]
    B3[2, 3] = dNdr[1]
    B3[2, 5] = dNdr[2]
    B3[2, 7] = dNdr[3]
    B3[3, 1] = dNds[0]
    B3[3, 3] = dNds[1]
    B3[3, 5] = dNds[2]
    B3[3, 7] = dNds[3]

    B = B1*B2*B3
    return B

def planeStressC(E,nu):# 弹性系数矩阵
    C = np.zeros((3,3))
    cons = E/(1+nu)
    C[0, 0] = C[1, 1] = cons*1/(1-nu)
    C[0, 1] = C[1, 0] = cons * nu / (1 - nu)
    C[2, 2] = cons * 1 / 2
    return C

intPoint = [-1/sqrt(3), 1/sqrt(3)]# 二阶高斯点坐标
weight = [1.0, 1.0]# 权重

x = [-1, 1, 1, -1]
y = [-1, -1, 1, 1]

E = 1
nu = 0.3
C = planeStressC(E,nu)

K = np.zeros((8,8))
for j in range(0, 2): # 数值积分求k
    for i in range(0, 2):
        r = intPoint[i]
        s = intPoint[j]
        Jinv, Jdet = jacobian(x, y, r, s)
        B = Bmatrix(r, s, Jinv)
        BT = np.transpose(B)
        tmp = BT*C*B*Jdet
        K = K + tmp

print('Full integration of K matrix:')
print(K) # K和x, y, E, nu有关
print(np.linalg.det(K))


# 力和位移边界条件
# U = np.array([0, 0, 0, 0, "u_unknow", "u_unknow", "u_unknow", "u_unknow"])
# F = np.array(["F_unknow", "F_unknow", "F_unknow", "F_unknow", 0, -1000, 1000, 0])

new_K = K[4:8, 4:8]
new_F = np.matrix([[0],[1000],[-1000],[0]])# 力边界条件
new1_U = np.linalg.solve(new_K, new_F) #用自带函数解方程
# new_U = my_LUsolve(new_K, new_F) #用LU解

print("new1_U:")
print(new1_U)
# print("new_U:")
# print(new_U)

U = np.zeros((8,1))
U[4, 0] =new1_U[0][0]
U[5, 0] =new1_U[1][0]
U[6, 0] =new1_U[2][0]
U[7, 0] =new1_U[3][0]
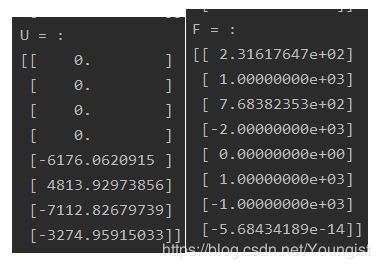
print("U = :")
print(U)
F = K*U
print("F = :")
print(F)

4、还在整理4单元9节点总刚度矩阵的组装，之后会写出来，编的比较粗糙，还请谅解哈哈哈！

5、哇都忘记截答案了，补上！

结果如下：

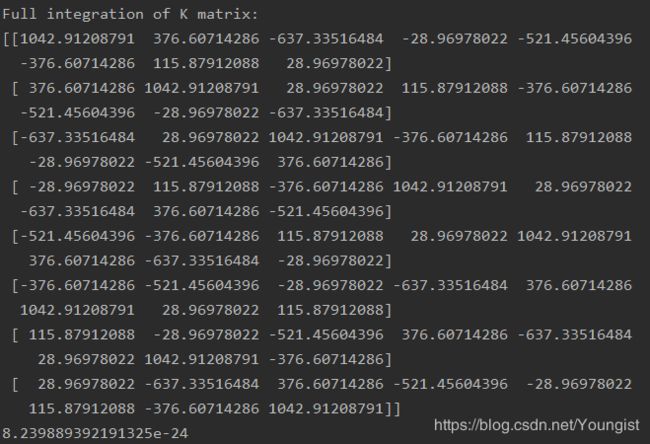
这里发现Kdet=0，K矩阵为奇异矩阵！