第十届蓝桥杯大赛软件类省赛
其他组见以下链接。
第十届蓝桥杯所有的题
一、研究生组
试题 A: 立方和
本题总分:5 分
【问题描述】
小明对数位中含有 2、0、1、9 的数字很感兴趣,在 1 到 40 中这样的数包
括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574,平方和是 14362,
立方和是 400816。
请问,在 1 到 2019 中,所有这样的数的立方和是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 B: 字串数字
本题总分:5 分
【问题描述】
小明用字母 A 对应数字 1,B 对应 2,以此类推,用 Z 对应 26。对于 27
以上的数字,小明用两位或更长位的字符串来对应,例如 AA 对应 27,AB 对
应 28,AZ 对应 52,LQ 对应 329。
请问 LANQIAO 对应的数字是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 C: 质数
本题总分:10 分
【问题描述】
我们知道第一个质数是 2、第二个质数是 3、第三个质数是 5……请你计算
第 2019 个质数是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 D: 最短路
本题总分:10 分
【问题描述】
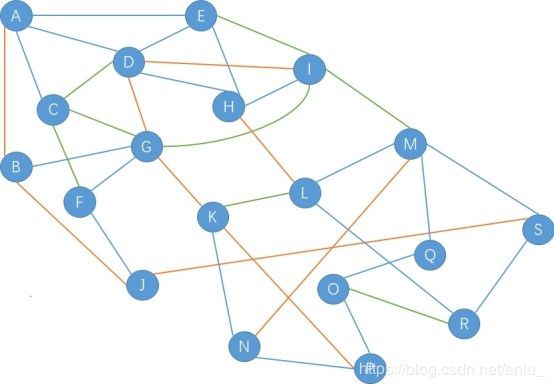
如下图所示,G 是一个无向图,其中蓝色边的长度是 1、橘色边的长度是2、绿色边的长度是 3。
则从 A 到 S 的最短距离是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 E: RSA 解密
本题总分:15 分
【问题描述】
RSA 是一种经典的加密算法。它的基本加密过程如下。
首先生成两个质数 p, q,令 n = p · q,设 d 与 (p − 1) · (q − 1) 互质,则可
找到 e 使得 d · e 除 (p − 1) · (q − 1) 的余数为 1。
n, d, e 组成了私钥,n, d 组成了公钥。
当使用公钥加密一个整数 X 时(小于 n),计算 C = Xd mod n,则 C 是加
密后的密文。
当收到密文 C 时,可使用私钥解开,计算公式为 X = Ce mod n。
例如,当 p = 5, q = 11, d = 3 时,n = 55, e = 27。
若加密数字 24,得 243 mod 55 = 19。
解密数字 19,得 1927 mod 55 = 24。
现在你知道公钥中 n = 1001733993063167141, d = 212353,同时你截获了
别人发送的密文 C = 20190324,请问,原文是多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 F: Fibonacci 数列与黄金分割
时间限制: 1.0s
内存限制: 256.0MB
本题总分:15 分
【问题描述】
Fibonacci 数列是非常著名的数列:
F[1] = 1,
F[2] = 1,
对于 i > 3,F[i] = F[i − 1] + F[i − 2]
Fibonacci 数列有一个特殊的性质,前一项与后一项的比值,F[i]/F[i + 1],
会趋近于黄金分割。
为了验证这一性质,给定正整数 N,请你计算 F[N]/F[N + 1],并保留 8 位
小数。
【输入格式】
一个正整数 N。(1 ≤ N ≤ 2000000000)
【输出格式】
F[N]/F[N + 1]。答案保留 8 位小数。
【样例输入】
2
【样例输出】
0.50000000
试题 G: 扫地机器人
时间限制: 1.0s
内存限制: 256.0MB
本题总分:20 分
【问题描述】
小明公司的办公区有一条长长的走廊,由 N 个方格区域组成,如下图所
示。
走廊内部署了 K 台扫地机器人,其中第 i 台在第 Ai 个方格区域中。
已知扫地机器人每分钟可以移动到左右相邻的方格中,并将该区域清扫干
净。
请你编写一个程序,计算每台机器人的清扫路线,使得
-
它们最终都返回出发方格,
-
每个方格区域都至少被清扫一遍,
-
从机器人开始行动到最后一台机器人归位花费的时间最少。
注意多台机器人可以同时清扫同一方块区域,它们不会互相影响。
输出最少花费的时间。
在上图所示的例子中,最少花费时间是 6。第一台路线:2-1-2-3-4-3-2,清
扫了 1、2、3、4 号区域。第二台路线 5-6-7-6-5,清扫了 5、6、7。第三台路线
10-9-8-9-10,清扫了 8、9 和 10。
【输入格式】
第一行包含两个整数 N 和 K。
接下来 K 行,每行一个整数 Ai。
【输出格式】
输出一个整数表示答案。
【样例输入】
10 3
5
2
10
【样例输出】
6
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ K < N ≤ 10。
对于 60% 的评测用例,1 ≤ K < N ≤ 1000。
对于所有评测用例,1 ≤ K < N ≤ 100000,1 ≤ Ai ≤ N。
试题 H: 修改数组
时间限制: 1.0s
内存限制: 256.0MB
本题总分:20 分
【问题描述】
给定一个长度为 N 的数组 A = [A1, A2, · · · AN],数组中有可能有重复出现
的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改
A2, A3, · · · , AN。
当修改 Ai 时,小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过,则
小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直
到 Ai 没有在 A1 ∼ Ai−1 中出现过。
当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
现在给定初始的 A 数组,请你计算出最终的 A 数组。
【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, · · · , AN 。
【输出格式】
输出 N 个整数,依次是最终的 A1, A2, · · · , AN。
【样例输入】
5
21134
【样例输出】
21345
【评测用例规模与约定】
对于 80% 的评测用例,1 ≤ N ≤ 10000。
对于所有评测用例,1 ≤ N ≤ 100000,1 ≤ Ai ≤ 1000000。
试题 I: 灵能传输
时间限制: 1.0s
内存限制: 256.0MB
本题总分:25 分
【题目背景】
在游戏《星际争霸 II》中,高阶圣堂武士作为星灵的重要 AOE 单位,在
游戏的中后期发挥着重要的作用,其技能”灵能风暴“可以消耗大量的灵能对
一片区域内的敌军造成毁灭性的伤害。经常用于对抗人类的生化部队和虫族的
刺蛇飞龙等低血量单位。
【问题描述】
你控制着 n 名高阶圣堂武士,方便起见标为 1, 2, · · · , n。每名高阶圣堂武士
需要一定的灵能来战斗,每个人有一个灵能值 ai 表示其拥有的灵能的多少(ai
非负表示这名高阶圣堂武士比在最佳状态下多余了 ai 点灵能,ai 为负则表示这
名高阶圣堂武士还需要 −ai 点灵能才能到达最佳战斗状态)。现在系统赋予了
你的高阶圣堂武士一个能力,传递灵能,每次你可以选择一个 i ∈ [2, n − 1],若
ai ≥ 0 则其两旁的高阶圣堂武士,也就是 i − 1、i + 1 这两名高阶圣堂武士会从
i 这名高阶圣堂武士这里各抽取 ai 点灵能;若 ai < 0 则其两旁的高阶圣堂武士,
也就是 i − 1, i + 1 这两名高阶圣堂武士会给 i 这名高阶圣堂武士 −ai 点灵能。形
式化来讲就是 ai−1+ = ai, ai+1+ = ai, ai− = 2ai。
灵能是非常高效的作战工具,同时也非常危险且不稳定,一位高阶圣堂
武士拥有的灵能过多或者过少都不好,定义一组高阶圣堂武士的不稳定度为
maxin=1|ai|,请你通过不限次数的传递灵能操作使得你控制的这一组高阶圣堂武
士的不稳定度最小。
【输入格式】
本题包含多组询问。输入的第一行包含一个正整数 T 表示询问组数。
接下来依次输入每一组询问。
每组询问的第一行包含一个正整数 n,表示高阶圣堂武士的数量。
接下来一行包含 n 个数 a1, a2, · · · , an。
【输出格式】
输出 T 行。每行一个整数依次表示每组询问的答案。
【样例输入】
3
3
5 -2 3
4
0000
3
123
【样例输出】
3
0
3
【样例说明】
对于第一组询问:
对 2 号高阶圣堂武士进行传输操作后 a1 = 3,a2 = 2,a3 = 1。答案为 3。
对于第二组询问:
这一组高阶圣堂武士拥有的灵能都正好可以让他们达到最佳战斗状态。
【样例输入】
3
4
-1 -2 -3 7
4
2 3 4 -8
5
-1 -1 6 -1 -1
【样例输出】
5
7
4
【样例输入】
见文件trans3.in。
【样例输出】
见文件trans3.ans。
【数据规模与约定】
对于所有评测用例,T ≤ 3,3 ≤ n ≤ 300000,|ai| ≤ 109。
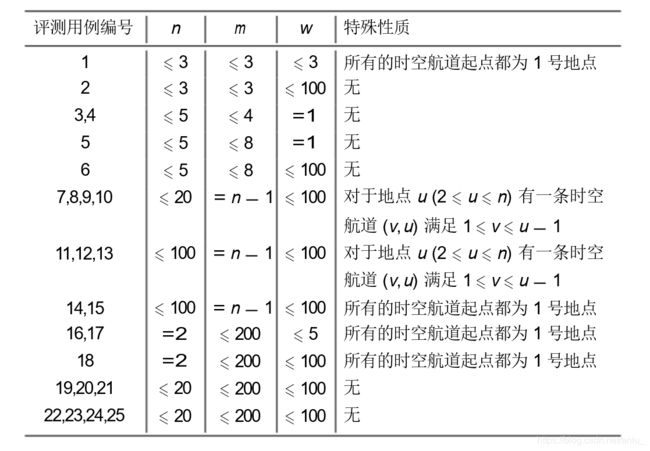
评测时将使用 25 个评测用例测试你的程序,每个评测用例的限制如下:
注意:本题输入量较大请使用快速的读入方式。
试题 J: 空间跳跃
时间限制: 1.0s
内存限制: 256.0MB
本题总分:25 分
【题目背景】
在游戏《星际争霸 II》中,战列巡航舰作为人类的终极作战武器,在后期
以及一些中期战术中发挥着空中堡垒的作用,其 “战术跳跃” 技能能让其在游戏
中期在敌军基地上空造成打击之后在血量较低时撤离,进行无战损骚扰,在人
类 vs 异虫对抗中经常用来压制异虫中期的发展。
【问题描述】
你在玩一个游戏,游戏中有 n 个地点和 m 条单向时空航道。每条时空航道
形如 (u, v, w, x),其中 u,v 表示这条时空航道的起点终点,w 表示通过这条航
道需要的时间(注意这个时间是现实当中游戏者的时间也是游戏内的时间),x
表示这条航道使用的频繁程度。时空航道不会成环,但可能会有两条航道的起
点相同同时终点也相同。游戏开始的时候,你的战列巡航舰到达了地点 1,每
当你到达一个地点的时候,战舰的电脑会按照每个起点为该地点的时空航道的
频繁程度随机选择一个航道并花费 w 单位时间到达该航道的终点。具体来说,
对于一个时间点 u,假如有 k 个起点为该地点的时空航道,他们的频繁程度分
别为 x1, x2, x3, · · · xk,那么选择第 i 个航道的概率就是
你的目的是在 L单位游戏时间内到达一个没有任何以该地点为起点的时空航道的地点。当
然你可以在到达某一个地点时重新开始游戏,如果你重新开始这个游戏,你就能回到游戏
开始的那一刻(即 1 号地点)并重置游戏内的时间(即你又可以有 L 单位的时间去跳跃
了),你也可以在没有任何以该地点为起点的地点重新开始,且无次数限制。你需要最小
化你在现实中花费的时间。当然在你运气足够好的情况下,你一定可以达成游戏目标。保
证一定有至少一条以 1 号地点为起点的航道。
请阅读样例以更清晰地理解题意。
【样例输出】
9.3333333333
【样例输入】
5 7 12
1355
4579
2581
3544
1233
3431
2425
【样例输出】
11.3571428571
【样例输入】
见文件jump4.in。
【样例输出】
见文件jump4.ans。
【数据规模与约定】
对于所有评测用例,2 ≤ n ≤ 100,1 ≤ m ≤ 200,w, x ≤ 100,0 ≤ L ≤ 109,
保证输入的图无环,答案不超过 109。
评测时将使用 25 个评测用例测试你的程序,每个评测用例的限制如下: