Python进行有限元编程-平面应力问题（三节点三角形单元）

参考书籍是：《有限元方法基础教程》（国际单位制）（第五版）

章节为：第6章 建立平面应力和平面应变刚度方程

重要的事情继续强调（有限元的基本计算流程）：

Step 1: 选择单元类型。

Step 2: 选择位移函数。

Step 3: 定义应变/位移和 应力/应变关系。

Step 4: 推导单元刚度矩阵和方程。

Step 5: 组合单元刚度方程得出总体方程并引进边界条件。

Step 6: 求解未知自由度。

Step 7:求解单元应变和应力。

Step 8: 解释结果。

 

==> 关于三节点三角形单元的刚度矩阵的推导过程，详见《有限元方法基础教程》第6章 建立平面应力和平面应变刚度方程

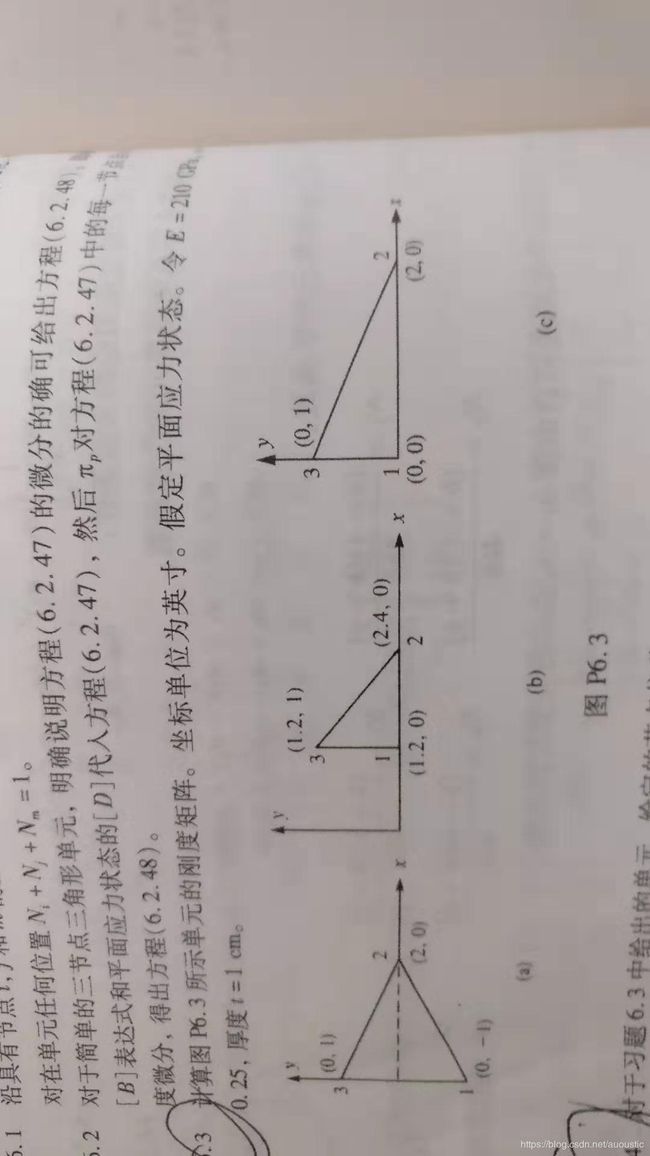
==> 本次主要计算的问题见上图。

==> 首先创建一个单元类。

==> 关于python中的构造函数（__init__方法）（因为之前学习java程序，java程序有一个构造函数的说法）传入的参数包括：三节点的坐标，和杨氏模量，泊松比，以及单元的厚度。（单元的面积是根据节点的坐标计算出来的）

import numpy as np

class T3(object):
    # 接下来首先创建类的构造函数 __init__
    # 对传入的参数进行说明，需要传入单元节点的坐标数据 coordinates
    # 传入材料的杨氏模量E； 材料的泊松比 v
    # 单元的厚度 t. 
    
    def __init__(self, coors, E, v, t):
        self.coors = coors
        self.E = E
        self.v = v
        self.t = t
        self.B = None
        self.D = None
        self.A = None

 

在初始化中，我们给当前单元增加了B矩阵，D矩阵，A（单元面积）作为当前单元类的属性（attribute）。

==> 首先计算出对应的B矩阵，B矩阵的推导公式见《有限元方法基础教程》。（B矩阵是由N矩阵求偏导得来的）。

 def Bmat(self):
        # coors中的数据排列规则是 x_i, x_j, x_m, y_i, y_j, y_m
        x_i, x_j, x_m, y_i, y_j, y_m = self.coors
        # 首先计算出当前对应的行列式
        A2 = x_i * (y_j - y_m) + x_j*(y_m - y_i) + x_m*(y_i - y_j)
        # 然后计算生成对应的a_i, a_j, a_m
        a_i = x_j * y_m - y_j * x_m
        a_j = y_i * x_m - x_i * y_m
        a_m = x_i * y_j - y_i * x_j
        
        # 计算生成对应的beta
        b_i = y_j - y_m
        b_j = y_m - y_i
        b_m = y_i - y_j
        
        # 计算生成对应的r_i, r_j, r_m
        r_i = x_m - x_j
        r_j = x_i - x_m
        r_m = x_j - x_i
        
        # 然后将上述的所有的数据组合成B矩阵
        B = np.zeros((3, 6), dtype=np.float32)
        B[0][0] = b_i
        B[0][2] = b_j
        B[0][4] = b_m
        
        # 然后添加r数据
        B[1][1] = r_i
        B[1][3] = r_j
        B[1][5] = r_m
        # 然后下面添加对应的b和r数据
        B[2][0] = r_i
        B[2][1] = b_i
        B[2][2] = r_j
        B[2][3] = b_j
        B[2][4] = r_m
        B[2][5] = b_m
        return A2/2, B/A2

 

此处不仅计算出了B矩阵，还有当前单元的面积。这在单元刚度矩阵的公式中仍有应用。

==> 接下来是计算出对应的D矩阵，D矩阵是应力，应变关系的矩阵，本文主要是针对平面应力问题（注意区分平面应力问题和平面应变问题，两者最主要的区别，可以按照如下的规则：在3D问题中的，当有一个方向上的尺寸远小于另外两个方向上的尺寸时，可将该问题简化为平面应力问题；当有一个方向上的尺寸远大于另外两个方向上的尺寸时，可将该问题简化为平面应变问题）

  # 接下来创建一个函数，来生成对应的D矩阵
    def Dmat(self):
        # 对于三角形三节点的，生成的D矩阵是3*3
        D = np.array([[1, self.v, 0], 
                      [self.v, 1, 0], 
                      [0, 0, (1-self.v)/2]])
        return D * self.E / (1 - self.v**2)

 

==> 对应于三节点三角形单元，其对应的单元刚度矩阵的表达式可以写为如下形式：

【k】= 【B】^T * 【D】 * 【B】 *  t * A;

==>这里我们需要计算B矩阵的转置矩阵，可以调用numpy中对于矩阵的转置操作; 也可以自己添加转置操作。

    def transpose(self, target:(list, np.ndarray)):
        # 首先把target包装成np.ndarray
        if isinstance(target, list):
            target = np.array(target)
        # 然后创建一个新的数据内存
        Tmat = np.zeros((target.shape[1], target.shape[0]), dtype=np.float32)
        # 然后给Tmat进行遍历赋值
        for row in range(target.shape[0]):
            for col in range(target.shape[1]):
                Tmat[col][row] = target[row][col]
        return Tmat

 

接下来创建一个生成单元刚度矩阵的函数。

  def stiffness_Matrix(self):
        # 这里我么首先需要获取B矩阵
        if self.B == None or self.A == None:
            A, B = self.Bmat()
            self.A = A
            self.B = B
        # 接下来获取对应的转置矩阵B_T
        B_T = self.transpose(self.B)
        # 然后获取D矩阵
        if self.D == None:
            D = self.Dmat()
            self.D = D
        # 首先进行B_T矩阵与D矩阵的相乘
        # 创建一个内存空间
        Mat_1 = np.zeros((B_T.shape[0], self.D.shape[1]), dtype=np.float32)
        # 创建一个临时求和变量
        sum_value = 0
        # 然后接下来便是来计算出对应的数值
        for row in range(B_T.shape[0]):
            for col in range(self.D.shape[1]):
                sum_value = 0
                for n in range(B_T.shape[1]):
                    sum_value += B_T[row][n] * self.D[n][col]
                else:
                    # 迭代结束后，当前位置的数据便计算完成了
                    Mat_1[row][col] = sum_value
        # 循环结束后，当前的矩阵相乘便计算完毕了
        # 接下来继续处理Mat_1矩阵和B矩阵相乘的计算过程
        # 开辟内存空间
        Mat_2 = np.zeros((Mat_1.shape[0], self.B.shape[1]), dtype=np.float32)
        for row in range(Mat_1.shape[0]):
            for col in range(self.B.shape[1]):
                sum_value = 0
                for n in range(Mat_1.shape[1]):
                    sum_value += Mat_1[row][n] * self.B[n][col]
                else:
                    Mat_2[row][col] = sum_value
        
        # 矩阵乘积结束之后，需要做的是去乘t
        return Mat_2 * self.t * A

 

==> 将上述问题的坐标信息输入到程序中去，得到对应的单元刚度矩阵。

对比书上的课后答案如下：

 

扶贫方式如下：