教你复现顶会论文网络结构(一)--DCN模型网络结构(Keras)
参考文章:
1、https://blog.csdn.net/roguesir/article/details/79763204
2、论文:https://arxiv.org/abs/1708.05123
3、https://www.jianshu.com/p/77719fc252fa
4、https://zhuanlan.zhihu.com/p/55234968 edition=yidianzixun&utm_source=yidianzixun&yidian_docid=0L8oiFUo
概述
该系列主要是复现一些经典的网络结构与顶会论文的网络结构,我一开始看论文,以为看到网络结构和了解结构原理后,就完全学到了这篇论文的精髓,谁知,等到自己想要用这个网络结构时,无法打通理解与代码复现的这一步,这就导致我在科研或者工作时的束手无措,因此,我就决定探究如何将一篇论文中的结构和论文中的公式用代码的形式复现出来。
深度学习框架:tensorflow2.0 keras(会侧重在Keras),numpy。
语言:python。
复现的代码全部在:https://github.com/Snail110/recsys。
0.介绍
本文介绍斯坦福与Google联合发表在AdKDD 2017上的论文《Deep & Cross Network for Ad Click Predictions》。这篇论文是Google 对 Wide & Deep工作的一个后续研究,文中提出 Deep & Cross Network,将Wide部分替换为由特殊网络结构实现的Cross,自动构造有限高阶的交叉特征,并学习对应权重,告别了繁琐的人工叉乘。文章发表后业界就有一些公司效仿此结构并应用于自身业务,成为其模型更新迭代中的一环。
1.网络结构
该部分主要是将论文中公式与结构图对应起来,理解每一个公式的含义以及网络结构图中每一部分的输入输出。

首先,当你看完一篇论文并理解了论文的主要思想后,需要尝试着将网络结构与论文中的每一步的数学公式一一对应上,在心中或者图片上协商每一个环节的数学公式,然后考虑用深度学习框架来实现。
首先这篇论文中有数学公式(1),(2),(3),(4),(5),(6)对应着网络模型。
然后需要一步一步的将公式对应到网络模型中,
公式(1)

说的是embedding过程,那么对应着网络图中是Spare feature到Embedding vec。属于比较常见的将稀疏特征转换成稠密特征的过程,但是在这里需要注意的是每一个field的embedding的长度需要计算得到:每个categorical特征嵌入维度为: 6 ∗ ( c a t e g o r y ) 1 / 4 6*(category)^{1/4} 6∗(category)1/4 category是每field的unique个数。
公式(2)
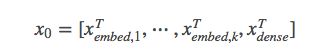
公式2中表示将embedding的向量与稠密向量拼接在一起,主要是讲稀疏特征域数值型特征拼接在一起。对应图二就是 embedding and stacking layer。
公式(3)
![]()
这个公式是本篇论文的核心思想,是cross network的参数更新环节。 x 0 x_{0} x0是公式2中的输出,同时是公式3的输入, x l x_{l} xl表示l层的输入, x l + 1 x_{l+1} xl+1表示l层的输出及l+1的输入。因此公式3对应着图中cross部分。
公式(4)
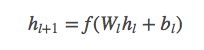
公式4是常见的deep的全连接层的参数更新公式,不需要过多解释,对应着图中的deep部分。
公式(5)

公式5是在deep部分输出和cross输出后的计算公式,对应着combination layer层。
2.代码复现
该部分主要是按照网络结构图,用代码的方式实现。在代码实现的过程中,我们需要紧紧结合数学公式体会其中的含义以及如何用代码来实现这些数学公式。
我是基于数据集:https://www.kaggle.com/c/porto-seguro-safe-driver-prediction来实现的。
Embedding and stacking layer
这部分主要是实现 sparse 到embedding vector过程以及数值型vector’和embedding vector之间的拼接。
from keras import layers
from keras.layers import Input,Dense,Embedding,Reshape,Add,Flatten,merge,Lambda,concatenate
from keras.optimizers import Adam
from keras.models import Model
from keras.utils import plot_model, np_utils
# from sklearn.preprocessing import OneHotEncoder,StandarScaler
from sklearn.metrics import accuracy_score
import random
from keras import backend as K
这里采用的是keras框架,那么从sparse 到embedding vector 我们用的keras.layers.Embedding函数。
def embedding_input(name,input_dim,output_dim):
# embedding的输入和输出
inp = Input(shape = (1,),dtype = 'int64',name = name)
# 对应公式1
embeddings = Embedding(input_dim,output_dim,input_length =1)(inp)
return inp,embeddings
def continus_input(name):
# 数值型 vec的输入与输出
inp = Input(shape=(1,),dtype = 'float32',name = name)
return inp, Reshape((1,1))(inp)
由于不同的sparse特征具有不同的长度,则embedding_layer函数需要迭代这些特征,一一进行设置输入大小与输出大小,然后将这sparse特征和数值型特征进行拼接。
def embedding_layers(fd):
# 该函数主要是定义输入和embedding输入的网络层
embeddings_tensors = []
continus_tensors = []
cate_feature = fd.feat_cate_len
numeric_feature = fd.numeric_cols
for ec in cate_feature:
layer_name = ec + '_inp'
# for categorical features, embedding特征在维度保持在6×(category cardinality)**(1/4)
embed_dim = cate_feature[ec] if int(6 * np.power(cate_feature[ec],1/4)) > cate_feature[ec] else int(6 * np.power(cate_feature[ec],1/4))
t_inp, t_embedding = embedding_input(layer_name,cate_feature[ec],embed_dim)
embeddings_tensors.append((t_inp,t_embedding))
del (t_inp, t_embedding)
for cc in numeric_feature:
layer_name = cc +'_in'
t_inp,t_build = continus_input(layer_name)
continus_tensors.append((t_inp,t_build))
del (t_inp,t_build)
# category feature的输入 这里的输入特征顺序一致 对应公式2
inp_layer = [et[0] for et in embeddings_tensors]
inp_embed = [et[1] for et in embeddings_tensors]
# numeric feature的输入
inp_layer += [ct[0] for ct in continus_tensors]
inp_embed += [ct[1] for ct in continus_tensors]
return inp_layer,inp_embed
Cross Layer
该部分主要是定义交叉层代码,主要实现公式3,**在这里需要注意是公式3的矩阵乘法是 x 0 x_{0} x0 x T x^{T} xTW,但是在我们实现代码的时候需要先计算 x T x^{T} xTW,这样的结果是得到度下降很多值,大大节省内存,降低计算量。
( x 0 x_{0} x0 x T x^{T} xT)W = x 0 x_{0} x0( x T x^{T} xT*W)
class CrossLayer(layers.Layer):
def __init__(self,output_dim,num_layer,**kwargs):
self.output_dim = output_dim
self.num_layer = num_layer
super(CrossLayer,self).__init__(**kwargs)
def build(self,input_shape):
self.input_dim = input_shape[2]
self.W = []
self.bias = []
for i in range(self.num_layer):
self.W.append(self.add_weight(shape=[1,self.input_dim],initializer = 'glorot_uniform',name='w_{}'.format(i),trainable=True))
self.bias.append(self.add_weight(shape=[1,self.input_dim],initializer = 'zeros',name='b_{}'.format(i),trainable=True))
self.built = True
def call(self,input):
for i in range(self.num_layer):
if i==0:
# cross = Lambda(lambda x: Add()([K.sum(self.W[i]*K.batch_dot(K.reshape(x,(-1,self.input_dim,1)),x),axis=1,keepdims=True),self.bias[i],x]))(input)
# 这种方法利于内存释放,先计算矩阵中简单的计算 对应公式3
cross = Lambda(lambda x: K.batch_dot(K.dot(x,K.transpose(self.W[i])),x) + self.bias[i] + x)(input)
else:
# cross = Lambda(lambda x: Add()([K.sum(self.W[i]*K.batch_dot(K.reshape(x,(-1,self.input_dim,1)),input),axis=1,keepdims=True),self.bias[i],input]))(cross)
cross = Lambda(lambda x: K.batch_dot(K.dot(x,K.transpose(self.W[i])),input) + self.bias[i] + x)(cross)
return Flatten()(cross)
def compute_output_shape(self,input_shape):
return (None,self.output_dim)
Deep layer and Concatenate layer
def DCN(inp_layer,inp_embed):
inp = concatenate(inp_embed,axis=-1)
#deep layer 对应公式 4
for i in range(6):
if i ==0:
deep = Dense(272,activation='relu')(Flatten()(inp))
else:
deep = Dense(272,activation='relu')(deep)
cross = CrossLayer(output_dim = inp.shape[2],num_layer=8,name = "cross_layer")(inp)
# concat both layers 对应公式5
output = concatenate([deep,cross],axis=-1)
output = Dense(2,activation='sigmoid')(output)
model = Model(inp_layer,output)
return model
Loss function
def fit(model,X,y):
model = DCN(inp_layer,inp_embed)
print(model.summary())
model.compile(Adam(0.01),loss = 'binary_crossentropy',metrics = ['accuracy'])
model.fit([X[c] for c in X.columns],y,batch_size=256,epochs=10)
3.总结
你看,通过这样一步步将公式与代码对应起来,就好实现多了,对于不同的计算公式采用不同的函数需要多看文档,这样才可以选用正确的api。
最后,如果需要获取全部代码,请看下我的github上仓库:https://github.com/Snail110/recsys/blob/master/DCN-keras.ipynb
这里面是用keras框架来写的,其他目录也有tensorflow框架来写。如果觉得我实现的还不错,记得给我一个星星哦。