基于OpenCV的双目深度估计实现与改进
双目深度估计
一、传统方法
常用的方法有SAD匹配算法,BM算法,SGBM算法,GC算法
1.1、SAD算法
SAD(Sum of absolute differences)是一种图像匹配算法 ,基本思想是:差的绝对值之和。此算法常用于图像块匹配,将每个像素对应数值之差的绝对值求和,据此评估两个图像块的相似度。该算法快速、但并不精确,通常用于多级处理的初步筛选。
基本流程:
(1)构造一个小窗口,类似于卷积核;
(2)用窗口覆盖左边的图像,选择出窗口覆盖区域内的所有像素点;
(3)同样用窗口覆盖右边的图像并选择出覆盖区域的像素点;
(4)左边覆盖区域减去右边覆盖区域,并求出所有像素点灰度差的绝对值之和;
(5)移动右边图像的窗口,重复(3)-(4)的处理(这里有个搜索范围,超过这个范围跳出);
(6)找到这个范围内SAD值最小的窗口,即找到了左图锚点的最佳匹配的像素块。
1.2 BM算法
BM 算法对图像进行双向匹配,首先通过匹配代价在右图中计算得出匹配点。然后相同的原理及计算在左图中的匹配点。比较找到的左匹配点和源匹配点是否一致,如果你是,则匹配成功。
优点是速度很快,但是效果不佳。
基于OpenCV的实现
void BM()
{
IplImage * img1 = cvLoadImage("left.png",0);
IplImage * img2 = cvLoadImage("right.png",0);
CvStereoBMState* BMState=cvCreateStereoBMState();
assert(BMState);
BMState->preFilterSize=9;
BMState->preFilterCap=31;
BMState->SADWindowSize=15;
BMState->minDisparity=0;
BMState->numberOfDisparities=64;
BMState->textureThreshold=10;
BMState->uniquenessRatio=15;
BMState->speckleWindowSize=100;
BMState->speckleRange=32;
BMState->disp12MaxDiff=1;
CvMat* disp=cvCreateMat(img1->height,img1->width,CV_16S);
CvMat* vdisp=cvCreateMat(img1->height,img1->width,CV_8U);
int64 t=getTickCount();
cvFindStereoCorrespondenceBM(img1,img2,disp,BMState);
t=getTickCount()-t;
cout<<"Time elapsed:"<其中minDisparity是控制匹配搜索的第一个参数,代表了匹配搜苏从哪里开始,numberOfDisparities表示最大搜索视差数uniquenessRatio表示匹配功能函数,这三个参数比较重要,可以根据实验给予参数值 .
1.3 SGBM算法
OpenCV中的SGBM算法是一种半全局立体匹配算法,立体匹配的效果明显好于局部匹配算法,但是同时复杂度上也要远远大于局部匹配算法。算法主要是参考Stereo Processing by Semiglobal Matching and Mutual Information。 opencv中实现的SGBM算法计算匹配代价没有按照原始论文的互信息作为代价,而是按照块匹配的代价。
minDisparity:最小视差,默认为0。此参数决定左图中的像素点在右图匹配搜索的起点,int 类型;
**numDisparities:**视差搜索范围长度,其值必须为16的整数倍。最大视差 maxDisparity = minDisparity + numDisparities -1;
**blockSize:**SAD代价计算窗口大小,默认为5。窗口大小为奇数,一般在33 到2121之间;
**P1、P2:**能量函数参数,P1是相邻像素点视差增/减 1 时的惩罚系数;P2是相邻像素点视差变化值大于1时的惩罚系数。P2必须大于P1。需要指出,在动态规划时,P1和P2都是常数。
一般建议:
P1 = 8cnsgbm.SADWindowSizesgbm.SADWindowSize;P2 = 32cnsgbm.SADWindowSizesgbm.SADWindowSize;
实验总结:
- blockSize(SADWindowSize) 越小,也就是匹配代价计算的窗口越小,视差图噪声越大;blockSize越大,视差图越平滑;太大的size容易导致过平滑,并且误匹配增多,体现在视差图中空洞增多;
- 惩罚系数控制视差图的平滑度,P2>P1,P2越大则视差图越平滑;
- 八方向动态规划较五方向改善效果不明显,主要在图像边缘能够找到正确的匹配
1.4 GC算法
GC算法在OpenCV3中已经没有了相应的API,因为这种方法虽然效果好,但是计算量实在是太大,不实用。
二、深度学习方法
深度图除了应用传统方法计算之外,还可以通过最近几年非常火热的机器学习,深度学习等技术进行实现。目前在无人驾驶领域有迫切的应用。深度估计不仅仅可以用双目进行深度估计,甚至还可以用单目图像进行深度估计。双目深度估计在三维重建,HCI,AR,自动驾驶等领域至关重要,单目深度估计也有意义。尽管有不少硬件能够直接得到深度图,但它们都有各自的缺陷。比如3D LIDAR设备非常昂贵;基于结构光的深度摄像头比如Kinect等在室外无法使用,且得到的深度图噪声比较大;而双目摄像头需要利用立体匹配算法,计算量比较大,而且对于低纹理场景效果不好。单目摄像头相比来说成本最低,设备也较普及,所以从单目摄像头估计出深度仍然是一个可选的方案,应用比其它方案更加广泛。举个SLAM的例子,对于单目SLAM来说,从单张图(或者是静止的图序列)是无法在几何上得到深度的。如果能通过算法给出一个粗略的深度估计(相当于从数据集中获得图像的深度先验),对于算法的收敛性和鲁棒性也是一个很大的提升 。
2.1 PSMNet(双目)–CVPR2018
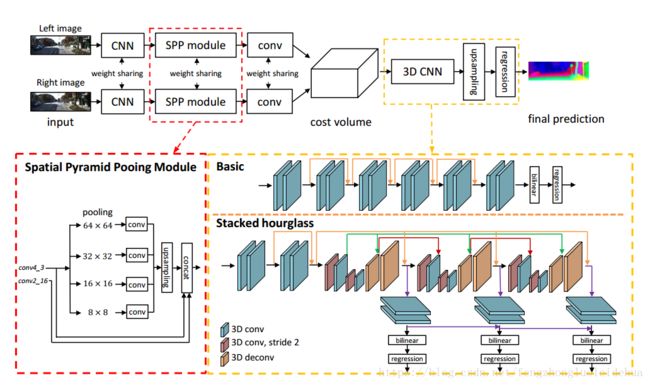
PSMNet(Pyramid Stereo Matching Network)是利用双目立体图像中进行深度估计的,它提出了一个全新的金字塔匹配网络在立体匹配中利用全局环境信息。空间金字塔池化(SPP)和空洞卷积(dilated convolution)用来扩大感受野。通过这个方法,PSMNet将像素级别的特征拓展到包含不同尺度感受野的区域级别的特征,将全局和局部特征信息结合起来构成匹配代价卷以获得更加可靠的视差估计值。除此之外,本文还设计了一个结合了中间监督的堆叠沙漏3D卷积神经网络去调整匹配代价卷(类似传统算法中的代价聚合过程)。这个堆叠的沙漏3D-CNN重复进行由精到粗再由粗到精(top-down/bottom-up)的过程来提高对全局信息的利用程度。
下图是PSMNet的整体网络结构:
其中最重要的部分是空间金字塔池化模块
单独从一个像素的强度(灰度或RGB值)很难判断环境关系。因此借助物体的环境信息来丰富图像特征能够有助于一致性估计,尤其对于不适定区域。在本文中,物体(例如汽车)和次级区域(车窗,轮胎等)的关系由SPP模块学习来结合多层级的环境信息。
在何凯明的论文中,SPP被设计用来去除CNN中的尺寸约束。由SPP生成的不同级别的特征图被平整后送入全卷积层用于分类,在此之后SPP被用于语义分割问题。ParseNet使用全局平均池化来结合全局环境信息。PSPNet拓展了ParseNet,采用包含不同尺度和次级区域信息的分层全局池化。在PSPNet中,SPP模块使用自适应平均池化把特征压缩到四个尺度上,并紧跟一个1*1的卷积层来减少特征维度,之后低维度的特征图通过双线性插值的方法进行上采样以恢复到原始图片的尺寸。不同级别的特征图都结合成最终的SPP特征图。
在本文中,我们为SPP设计了4个尺度的平均池化:6464,3232,1616,88。并与PSPNet一样,采用了1*1卷积和上采样。在简化模型测试中(ablation study),我们设计了大量的实验来展示不同级别的特征图的影响。
本文的实验结果在KITT数据集上取得了最好的成绩。
###2.2 DORN(单目)-CVPR2018
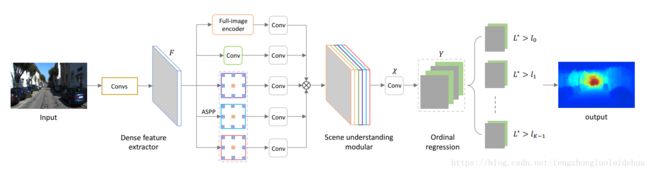
本文(Deep Ordinal Regression Network for Monocular Depth Estimation)是ROB2018中深度预测的冠军方案,它与传统的深度预测方法不同。传统的方法是利用视角、纹理、目标大小、目标位置、遮挡关系最为深度预测的特征线索;当前使用的基于深度卷积网络的方法大多采用的是用于图像分类的特征提取网络,这些网络由于有池化层的操作或者步长较大的卷积曹祖,导致预测的分辨率较低,虽然可以通过转置卷积、跨层连接等方式进行分辨率的方法,但是这样网络结构的复杂度和时间开销和计算成本相应增加 。本文提出的方案采用扩张卷积的方式进行多尺度融合。网络结构如下图:
这个方法中最重要的亮点是提出了多尺度融合方法。网络中的 ASPP部分采用不同扩张系数的扩张卷积操作,能够在不改变图像分辨率的前提下,有效得到不同感受野大小的卷积操作,进而得到多尺度融合特征
三、实验
由于SGBM算法视差效果好速度快的特点,常常被广泛应用和改进,所以我就没有对其他算法进行重新实现,只在Codeing Test中实验了SGBM算法,并对该算法进行了改进。
3.1 SGBM算法的实现
Mat SGBM(Mat left,Mat right)
{
Mat disp,color(disp.size(),CV_8UC3);
int mindisparity = 0;
int ndisparities = 64;
int SADWindowSize = 11;
//SGBM
cv::Ptr sgbm = cv::StereoSGBM::create(mindisparity, ndisparities, SADWindowSize);
int P1 = 8 * left.channels() * SADWindowSize* SADWindowSize;
int P2 = 32 * left.channels() * SADWindowSize* SADWindowSize;
sgbm->setP1(P1);
sgbm->setP2(P2);
sgbm->setPreFilterCap(15);
sgbm->setUniquenessRatio(10);
sgbm->setSpeckleRange(2);
sgbm->setSpeckleWindowSize(100);
sgbm->setDisp1
}
3.2 灰度转伪彩色
为了让实验效果更佳的明显,我对实验结果进行了彩色可视化,具体是算法试下如下:
Mat gray2Color(Mat img)
{
Mat img_color(img.rows, img.cols, CV_8UC3);//构造RGB图像
#define IMG_B(img,y,x) img.at(y,x)[0]
#define IMG_G(img,y,x) img.at(y,x)[1]
#define IMG_R(img,y,x) img.at(y,x)[2]
uchar tmp2=0;
for (int y=0;y(y,x);
if (tmp2 <= 51)
{
IMG_B(img_color,y,x) = 255;
IMG_G(img_color,y,x) = tmp2*5;
IMG_R(img_color,y,x) = 0;
}
else if (tmp2 <= 102)
{
tmp2-=51;
IMG_B(img_color,y,x) = 255-tmp2*5;
IMG_G(img_color,y,x) = 255;
IMG_R(img_color,y,x) = 0;
}
else if (tmp2 <= 153)
{
tmp2-=102;
IMG_B(img_color,y,x) = 0;
IMG_G(img_color,y,x) = 255;
IMG_R(img_color,y,x) = tmp2*5;
}
else if (tmp2 <= 204)
{
tmp2-=153;
IMG_B(img_color,y,x) = 0;
IMG_G(img_color,y,x) = 255-uchar(128.0*tmp2/51.0+0.5);
IMG_R(img_color,y,x) = 255;
}
else
{
tmp2-=204;
IMG_B(img_color,y,x) = 0;
IMG_G(img_color,y,x) = 127-uchar(127.0*tmp2/51.0+0.5);
IMG_R(img_color,y,x) = 255;
}
}
}
return img_color;
}
3.3 实验效果

3.2 对SGBM算法的改进
从上面的可视化深度图中可以看出,深度信息中存在许多的空洞,为了填充这些缺失的空洞值,对算法SGBM进行了改进。
改进思路:
① 以视差图dispImg为例。计算图像的积分图integral,并保存对应积分图中每个积分值处所有累加的像素点个数n(空洞处的像素点不计入n中,因为空洞处像素值为0,对积分值没有任何作用,反而会平滑图像)。
② 采用多层次均值滤波。首先以一个较大的初始窗口去做均值滤波(积分图实现均值滤波就不多做介绍了,可以参考我之前的一篇博客),将大区域的空洞赋值。然后下次滤波时,将窗口尺寸缩小为原来的一半,利用原来的积分图再次滤波,给较小的空洞赋值(覆盖原来的值);依次类推,直至窗口大小变为3x3,此时停止滤波,得到最终结果。
③ 多层次滤波考虑的是对于初始较大的空洞区域,需要参考更多的邻域值,如果采用较小的滤波窗口,不能够完全填充,而如果全部采用较大的窗口,则图像会被严重平滑。因此根据空洞的大小,不断调整滤波窗口。先用大窗口给所有空洞赋值,然后利用逐渐变成小窗口滤波覆盖原来的值,这样既能保证空洞能被填充上,也能保证图像不会被过度平滑。
算法实现:
//将噪声和空洞进行填充
Mat insertDepth32f(cv::Mat depth)
{
const int width = depth.cols;
const int height = depth.rows;
float* data = (float*)depth.data;
cv::Mat integralMap = cv::Mat::zeros(height, width, CV_64F);
cv::Mat ptsMap = cv::Mat::zeros(height, width, CV_32S);
double* integral = (double*)integralMap.data;
int* ptsIntegral = (int*)ptsMap.data;
memset(integral, 0, sizeof(double) * width * height);
memset(ptsIntegral, 0, sizeof(int) * width * height);
for (int i = 0; i < height; ++i)
{
int id1 = i * width;
for (int j = 0; j < width; ++j)
{
int id2 = id1 + j;
if (data[id2] > 1e-3)
{
integral[id2] = data[id2];
ptsIntegral[id2] = 1;
}
}
}
// 积分区间
for (int i = 0; i < height; ++i)
{
int id1 = i * width;
for (int j = 1; j < width; ++j)
{
int id2 = id1 + j;
integral[id2] += integral[id2 - 1];
ptsIntegral[id2] += ptsIntegral[id2 - 1];
}
}
for (int i = 1; i < height; ++i)
{
int id1 = i * width;
for (int j = 0; j < width; ++j)
{
int id2 = id1 + j;
integral[id2] += integral[id2 - width];
ptsIntegral[id2] += ptsIntegral[id2 - width];
}
}
int wnd;
double dWnd = 2;
while (dWnd > 1)
{
wnd = int(dWnd);
dWnd /= 2;
for (int i = 0; i < height; ++i)
{
int id1 = i * width;
for (int j = 0; j < width; ++j)
{
int id2 = id1 + j;
int left = j - wnd - 1;
int right = j + wnd;
int top = i - wnd - 1;
int bot = i + wnd;
left = max(0, left);
right = min(right, width - 1);
top = max(0, top);
bot = min(bot, height - 1);
int dx = right - left;
int dy = (bot - top) * width;
int idLeftTop = top * width + left;
int idRightTop = idLeftTop + dx;
int idLeftBot = idLeftTop + dy;
int idRightBot = idLeftBot + dx;
int ptsCnt = ptsIntegral[idRightBot] + ptsIntegral[idLeftTop] - (ptsIntegral[idLeftBot] + ptsIntegral[idRightTop]);
double sumGray = integral[idRightBot] + integral[idLeftTop] - (integral[idLeftBot] + integral[idRightTop]);
if (ptsCnt <= 0)
{
continue;
}
data[id2] = float(sumGray / ptsCnt);
}
}
return depth;
}
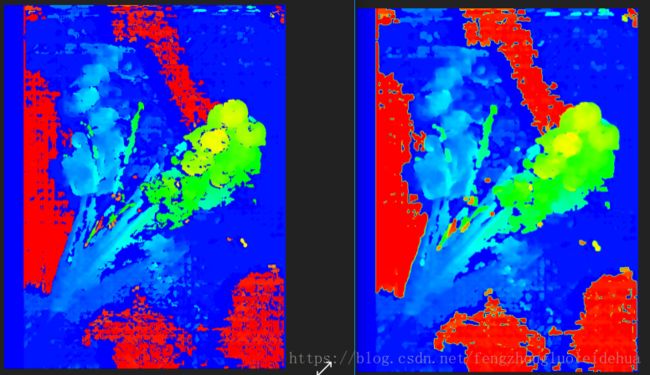
改进效果
通过实验发现,改进后的算法比原来的效果要好不少,例如图6中填充后的视差彩色图的噪声明显比没有填充的视差图少很多。说明改进之后还是很有效的。
四、总结
不管是传统方法还是深度学习的方法进行深度估计都有各自的优点,但是我更看好应用深度学习的方法。因为深度学习的方法可以学习到更多的特征,不仅仅是多尺度的特征还可以是多层次的特征。目前在自动驾驶领域应用的也多数是深度学习的方法进行深度估计,因为效果明显优于传统的方法。
##参考文献:
https://www.cnblogs.com/polly333/p/5130375.html
https://www.cnblogs.com/riddick/p/8486223.html?utm_source=debugrun&utm_medium=referral
Chang, Jia-Ren, and Yong-Sheng Chen. “Pyramid Stereo Matching Network.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
Fu, Huan, et al. “Deep Ordinal Regression Network for Monocular Depth Estimation.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.