【暖*墟】 #BFS# 广搜技巧与优化
BFS 广度优先搜索(队列)
目录
一. 基本实现
二. 双端队列
普通队列用于边权为定值的最短路搜索。
双端队列可以进行边权为1/0的最短路搜索。
【例题】洛谷 p2243 电路维修
三. Hash判重
1、哈希表的特征
2、哈希表的实现方法:拉链法
3、Hash的应用
4、散列法
【Hash表的常见构造方法】
【例题】洛谷 p2730 魔板
一. 基本实现
a .首先选择一个顶点作为起始结点,并将其染成灰色,其余结点为白色。
b. 将起始结点放入队列中。 并找出所有与之邻接的结点。
c. 从队列首部选出一个顶点,将找到的邻接结点放入队列尾部,
将已访问过结点涂成黑色。如果顶点的颜色是灰色,表示已经放入了队列,
如果顶点的颜色是白色,表示还没有发现 d. 按照同样的方法处理队列中的下一个结点。
基本就是出队的顶点变成黑色,在队列里的是灰色,还没入队的是白色。
例如,从顶点1开始进行广度优先搜索:
- 初始状态,从顶点1开始,队列={1}
- 访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
- 访问2的邻接结点,2出队,4入队,队列={3,4}
- 访问3的邻接结点,3出队,队列={4}
- 访问4的邻接结点,4出队,队列={ 空} 结点5对于1来说不可达。
二. 双端队列
普通队列用于边权为定值的最短路搜索。
且每次到达都是最优的决策(不用取min)。
因为所有状态按照 入队的先后顺序 具有 层次单调性,每次扩展,都往外走一步,
满足从起始到该状态的最优性(不用取min/也不用比大小,如果如此失去了意义)。
双端队列可以进行边权为1/0的最短路搜索。
对于一条边 u 到 v ,如果此边权值为0,我们将它 push_front(v) ,否则 push_back(k),
每次取队首,这样我们保证了单调性(即每次优先选择最优的)。
注意细节:把某一方格对角两点的连线看成边,若和原状态匹配边权为0,否则为1。
我们放入队列里的还有u,这样才能做到将每次取出的时候更新,
也就是说在队列中放入二元组(u,v)。复杂度:O(r*c)。
【例题】洛谷 p2243 电路维修
有一天 Mark 和James 的飞行车没有办法启动了,经过检查发现原来是电路板的故障。
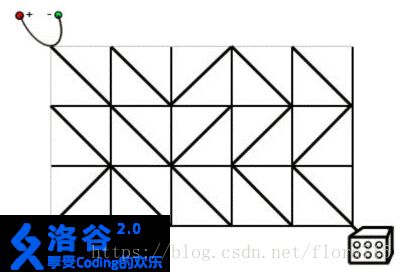
飞行车的电路板设计很奇葩,如下图所示:
对于每组测试数据,在单独的一行输出一个正整数,表示所需的缩小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出 NO SOLUTION。
#include
#include
#include
#include
#include
#include
#include (其中“\”的使用可见 这里 )
三. Hash判重
1、哈希表的特征
深搜中的【路径寻找问题】,常常可以用构造Hash表实现。
Hash是根据关键码值(Key value)而直接进行访问的数据结构。
它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。
这个映射函数叫做散列函数,存放记录的数组叫做散列表。
这里的对应关系 f 称为散列函数,又称为哈希(Hash函数),
散列将记录存储在一块连续的存储空间中,这块连续存储空间称为散列表或哈希表。
哈希表是把Key通过一个固定的算法函数,即所谓的哈希函数转换成一个整型数字,
然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,
将value存储在以该数字为下标的数组空间里。
(或:把任意长度的输入(又叫做预映射),通过散列算法,变换成固定长度的输出,
该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,
不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入值。
简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。)
而当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,
并定位到该空间获取value,如此一来,就可以充分利用到数组的定位性能进行数据定位。
2、哈希表的实现方法:拉链法
数组的特点是:寻址容易,插入和删除困难。
而链表的特点是:寻址困难,插入和删除容易。
一种寻址容易,且插入删除容易的数据结构:哈希表。
哈希表最常用的实现方法——拉链法,我们可以理解为“链表的数组”,如图:
![]()
左边很明显是数组,数组的每个成员包括一个指针,指向一个链表的头,
根据元素的一些特征把元素分配到不同的链表中去,再根据这些特征,找到正确的链表和元素。
3、Hash的应用
1、Hash主要用于信息安全领域中加密算法,它把一些不同长度的信息转化为128位编码,
这些编码值叫做Hash值。Hash即找到一种数据内容和数据存放地址之间的映射关系。
2、查找:哈希表,又称为散列,是一种更加快捷的查找技术。
我们之前的查找思路:集合中拿出来一个元素,比较,不等就缩小范围继续查找。
而哈希表是完全另外一种思路:知道key值可以直接计算出这个元素在集合中的位置。
3、Hash表在海量数据处理中有着广泛应用。
Hash Table的查询速度非常的快,几乎是O(1)的时间复杂度。
Q : 如果两个字符串在哈希表中对应的位置相同怎么办?
可以转化成链表来解决,只要在哈希表的每个入口挂一个链表,保存所有对应的字符串就OK了。
4、散列法
元素特征转变为数组下标的方法就是散列法。下面列出三种比较常用的:
1,除法散列法
最直观的一种,上图使用的就是这种散列法,公式形如: index = value % 16
2,平方散列法
求index是非常频繁的操作,而乘法的运算要比除法来得省时,
所以我们考虑把除法换成乘法和一个位移操作。公式: index = (value * value) >> 28
(右移,除以2^28。记法:左移变大,是乘。右移变小,是除。)
3,斐波那契(Fibonacci)散列法
找出一个理想的乘数,而不拿value本身当作乘数呢。
1)对于16位整数而言,这个乘数是40503
2)对于32位整数而言,这个乘数是2654435769
3)对于64位整数而言,这个乘数是11400714819323198485
这几个“理想乘数”是如何得出来的呢?这跟一个法则有关,叫黄金分割法则,
而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列,
即如此形式的序列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610…。
对我们常见的32位整数而言,公式: index = (value * 2654435769) >> 28
如果用这种斐波那契散列法的话,那上面的图就变成这样了:
![]()
注:用斐波那契散列法调整之后会比原来的取模散列法好很多。
【Hash表的常见构造方法】
- 状态压缩法——用二进制记录状态。
- 直接取余法——选取一个质数M作为除数。
- 平方取中法——计算关键值的平方,取中间的r位。
- 折叠法——把所有字符的ASCII码加起来。
【例题】洛谷 p2730 魔板
在成功地发明了魔方之后,鲁比克先生发明了它的二维版本,称作魔板。
这是一张有8个大小相同的格子的魔板:
1 2 3 4
8 7 6 5我们知道魔板的每一个方格都有一种颜色。这8种颜色用前8个正整数来表示。
可以用颜色的序列来表示一种魔板状态,规定从魔板的左上角开始,
沿顺时针方向依次取出整数,构成一个颜色序列。
对于上图的魔板基本状态,我们用序列(1,2,3,4,5,6,7,8)来表示。
提供三种基本操作,分别用大写字母“A”,“B”,“C”来表示 :
- “A”:交换上下两行;
- “B”:将最右边的一列插入最左边;
- “C”:魔板中央四格作顺时针旋转。
对于每种可能的状态,这三种基本操作都可以使用。
用最少的基本操作完成基本状态到目标状态的转换,输出基本操作序列。
【思路分析】广搜+判重。
这里的判重用 康托展开 的方法:
需要把每个搜索到的魔板状态加入队列的判重数组里面。
1、我们可能会想到将魔板的8个位置上的数字直接转换为8位数加入队列,
这样的话我们需要将每个魔板的8位置状态转换为一个8位数,
判重时需要长度近10^8的布尔数组,空间将近200M,MLE。
2、继续思考:魔板的所有排列方式共有8!=40320种,
如果把魔板的每一种排列方式都用某种方法遍上一个序号,
那么判重的时候就只需要长度略大于40000的布尔数组,空间少了很多。
3、那么到底应该怎么编号?先从简单一点的例子看起:
如果排列的数字只有1,2的时候,所有的排列方式为:(1,2),(2,1);
如果排列的数字有3个:1,2,3,可以根据排列的第一位数字进行分类:
第一位为1的排列:(1,2,3),(2,1,3),
第一位为2的排列:(2,1,3),(2,3,1),
第一位为3的排列:(3,1,2),(3,2,1);
那么规律就出来了:对于从1到n的排列,如果第1位数字为i,
这个排列的编号肯定在(i-1)*(n-1)!-i*(n-1)! 的范围内。
这样我们就可以把这个问题的规模缩小。
4、但是留下来的数字并不一定是1到(n-1),需要重新给它们排序吗?
其实上面的规律也可以这样解释:当排列的第一位数字为所有元素中第i大的数字时,
这个排列的编号在(i-1)(n-1)!-i(n-1)! 之间。
寻找当前排列中某个数的后方有多少个数字与它不组成升序序列,
就能够说明它是在后面所有元素中的第几位。
5、得到编号用的方程:(其中a[i]为当前未出现的元素中是排在第几个(从0开始))
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 。这就是康托展开。
【代码实现】
#include
#include
#include
#include
#include
using namespace std;
bool bb[9],b[50000];
int MS[9];
char re[10];
struct node{
int a[9];
int step,father;
char c;
}l[50000];
void print(node x){
int s=0;
while(x.father!=0){
re[++s]=x.c;
x=l[x.father];
}
for(int i=s;i>=1;i--){
printf("%c",re[i]);
}
return;
}
int fc(int x){
if(x==0)return 0;
if(x==1)return 1;
return x*fc(x-1);
}
inline int KT(node x){
int num=0;
for(int i=1;i<=8;i++){
int s=0;
for(int j=i+1;j<=8;j++){
if(x.a[i]>x.a[j])s++;
}
num+=s*fc(8-i);
}
return num;
}
inline void swapp(int &a,int &b)
{int c=a;a=b;b=c;}
node A(node),B(node),C(node);
int main(){
for(int i=1;i<=8;i++)scanf("%d",&MS[i]);
int head=0,tail=1;
for(int i=1;i<=9;i++)l[1].a[i-1]=i-1;
l[1].step=0;
l[1].father=0;
while(head=2;i--){
swapp(x.a[i-1],x.a[i]);
swapp(x.a[9-i],x.a[10-i]);
}
return x;
}
node C(node x){
swapp(x.a[3],x.a[2]);
swapp(x.a[7],x.a[6]);
swapp(x.a[2],x.a[6]);
return x;
}
——时间划过风的轨迹,那个少年,还在等你。