人工智能中的偏序规划-基于STRIPS语言

新增加了算法的形式化描述

引言

规划问题的定义

给定目标，建立能成就目标的动作序列的过程称为规划。本文所研究的问题是经典规划的研究内容，即完全客观的、静态的、确定性的、离散的环境。
规划问题可以形式化表示为 (S,A,G) 。其中 S 是用逻辑语句描述的状态集合，A是动作的集合，G是目标状态的一个部分描述。规划问题的解是初始状态到目标状态的动作序列。

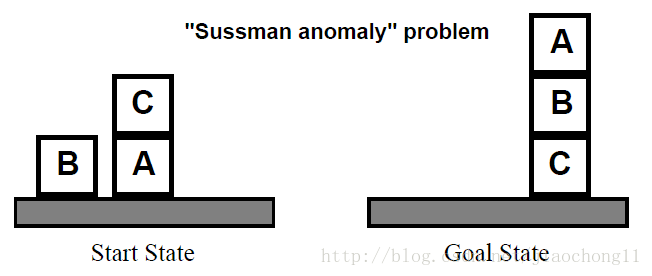
一个典型的规划问题是如图1的积木问题，通过规划可以找出从初始状态到目标状态的一条动作路径。

---

图1

本文主要内容

本文的主要内容是介绍基于STRIPS语言的偏序规划问题。主要内容包括如何使用规划语言描述实际规划问题和如何用偏序规划求解器对问题进行求解。最后通过积木问题的案例详细介绍了求解过程。

STRIPS规划语言

STRIPS（Stanford Research Institute Problem Solver）规划语言是最经典的一种规划语言，下面的规划问题也是基于STRIPS语言的描述。STRIPS语言包含三个要素：状态表示、目标表示和动作表示。

1. 状态表示
   状态表示为正文字的合取，具有以下特点：
   
   • 命题形式
   • 一阶形式：基项（无变量），无函数
   • 封闭世界假设：没有在状态中出现的文字都为假。
2. 目标表示
   目标表示为无变量正文字的合取。若状态S包含目标G中所有文字，则成状态S满足目标G
3. 动作表示
   动作表示包含以下三个部分。
   
   • Action(动作名，参数列表)
   • PreCondition：前提，表示为无函数正文字的合取。
   • Effect：效果，无函数文字的合取式。

STRIPS语言更多的了解可以参考基于STRIPS语言的经典规划

偏序规划

偏序规划的主要思想

偏序规划的主要思想是利用目标和动作的结构，使动作的搜索更加有效。偏序规划使用了一下假设：

1. 目标的结构为文字的合取式： L1∧L2∧...Ln 。偏序规划的基本思想是可以为每个目标 Li 构造子计划，然后集成形成完整的计划；
2. 动作与目标的相关性：偏序规划认为相关性可以作为动作的启发信息；
3. 集成子计划时应该利用到动作间的关系；

偏序规划的问题描述

偏序规划问题包含以下内容：

1. 动作集。初始条件下空规划的动作集表示为：{start， finish}其中，start的前提为空，效果就是初始状态。finish前提为规划的目标，效果为空。
2. 初始状态 start<finish ，其中 A<B 表示序约束，说明前者动作A必须在后者的动作B之前完成。　
3. 目标状态是找到动作序列 start<a1<a2<...<an<finish
4. 序约束： A<B 代表动作在时间上的先后关系
5. 因果链 A−→PB 表示P是A的效果，同时又是B的前提。若另外一个动作C效果为否定P，成为因果链冲突，那么动作C不应该出现在动作A和B之间，因此因果链也称保护时段。
6. 开前置条件：在部分计划中，如果还没有任何动作使得该前提条件为真，成该前置条件是开放的。

偏序规划生成器

一个偏序规划生成器的算法如下：

1. 生成初始规划： {start,finish} 和序 start<finish
2. 规划的扩展：
   在已经添加到规划的行动中选取一个动作的开前置条件P，然后选择任一动作A使得A的效果与P可合一，并通过下列方式保持一致性。
   
   • 如果A不在动作规划中，则将 A,Start<A,<A<finish 加入规划中。然后加入因果链 A−→PB 和序 A<B 。
   • 检查并消解冲突，包含以下两个方面：
     
     • 检查新的因果链 A−→PB 与所有已存在的动作之间的冲突；
     • 检查动作A与所有已存在的因果链的冲突
       消解冲突的方法为若动作Ｃ与因果链 A−→PB 冲突，那么应该添加序约束C < A　或者 B < C
3. 目标检查：开前置条件为空时，规划完成。

很多中文资料的算法都是这么给出的，这里对于初学者来说要注意两点：
1. 添加的行动可能会导致误解，算法是需要回溯的（添加地行动可能会撤销）;
2. 添加的行动可以是已经已经在动作规划中的行动，通过这些行动的添加可以增加新的因果链以及减少开前提条件(因为新的动作引入了新的开前提条件)。
3. 通过阅读形式化的算法描述会更加清楚算法求解过程。

---

完整的形式化的算法描述如下[2]：

积木问题的求解

这里我们通过一个具体的例子来深入了解偏序规划的工作过程。积木问题的初始状态和目标状态已经由图1给出。

---

问题的第一步是使用STRIPS语言对问题进行描述。积木问题的STRIPS语言描述如下：

Init{On(A,Table), On(C,A), On(B, Table),Block(B), Block(A), Block(C), Clear(B), Clear(C)}
Goal{On(A,B), On(B,C)}
Action{
  PutOn(b,x,y)
    PreCondition: On(b,x), Clear(b), Clear(y), Block(b), Block(y), b!=x b!=y x!=y
    Effect: On(b,y), Clear(x), ~On(b,x), ~Clear(y)
  PutOnTable(b,x)
    Precondition: On(b,x), Clear(b), Block(b), Block(x),b!=x
    Effect: On(b, Table), Clear(x), ~On(b,x)
}

进行偏序规划求解的步骤如下：

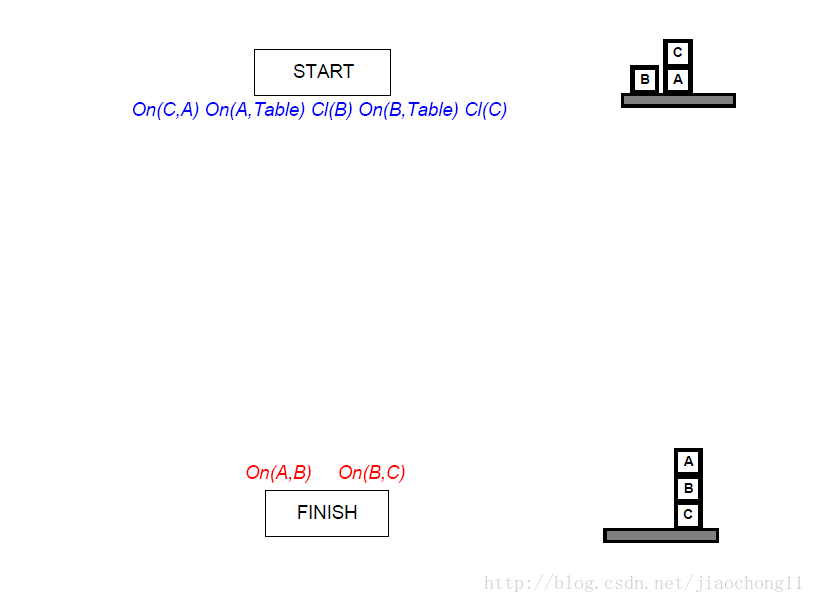
1. 初始化规划为{start, finish}，并添加序约束start < finish。如图2所示:

---

图2 初始状态

---

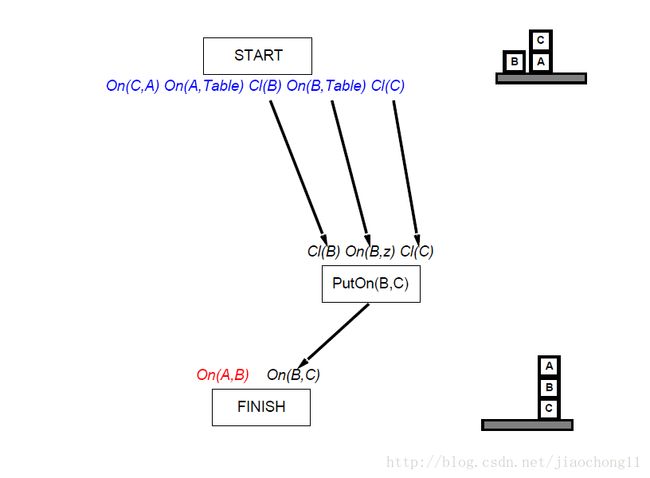
1. 从所有开前置条件{On(A,B), On(B,C)}中选择一个，这里我们选择On(B,C)。选择一个动作可以与On(B,C)合一。这里选择动作：PutOn(B,Table, C)，然后将动作PutOn(B,Table, C)和约束Start < PutOn(B, Table,C)和PutOn(B,Table,C) < Finish 添加到规划中，同时添加因果链 Start−→−−−−−−−−−−−−−−−−−Clear(B),On(B,Table),Clear(C)PutOn(B,Table,C) 以及 PutOn(B,Table,C)−→−−−On(A,B 。添加后状态如图3所示。

图3

---

1. 此时，剩余开前提条件只有On(A,B)。选择添加动作PutOn(A, Table, B)到规划图中。同时添加序约束Start < PutOn(A, Table, B)和PutOn(A, Table, B)< Finish 。这时需要检查冲突，经检查新添加动作与已存在的因果链 Start−→−−−−−−−−−−−−−−−−−Clear(B),On(B,Table),Clear(C)PutOn(B,Table,C) 冲突，冲突的原因是PutOn(A, Table, B)的效果否定了Clear(B)，因此需要添加序约束，使得PutOn(A, Table, B)在Start之前或者PutOn(B,Table,C)之后。这里由于Start < PutOn(A, Table, B)，因此必须添加约束PutOn(B,Table,C) < PutOn(A, Table, B)，当前的状态为如图4所示，绿色表示添加的序约束。
   
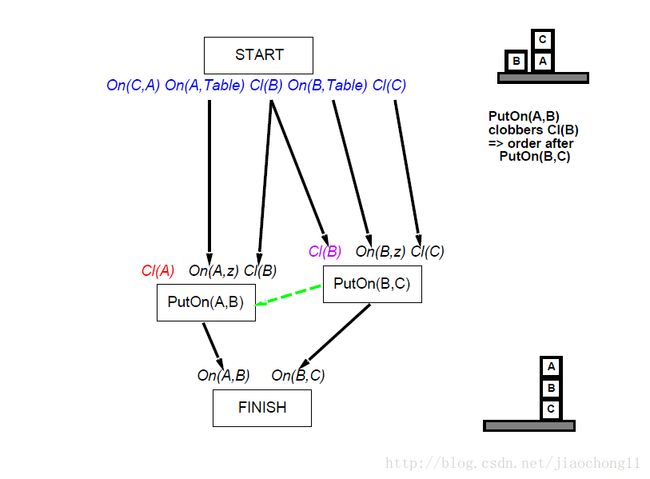
   图4

---

1. 添加动作PutOn(A,B)后，剩余的开前提条件为Clear(A)，这是可以添加动作PutOnTable(C,A)，添加序约束与因果链，同时检测冲突。这时的冲突为已有的动作PutOn(B,C)与要添加的因果链 Start−→−−−−−−−−−Clear(C),On(C,A)PutOnTable(C,A) ，冲突的原因是动作PutOn(B,C)的效果否定了效果Clear(C),因此需要添加序约束 PutOnTable(C,A)<PutOn(B,C) 。当前状态如图5所示：

---

图5

---

1. 此时，开前置条件为空，规划完成。规划得到的动作序列为：Start, PutOnTable(C,A), PutOn(B,C), PutOn(A,B), Finish。

1. 参考资料1:基于STRIPS语言的经典规划
2. 参考资料2: Intelligent Systems: Dale Schuurmans(第七章)